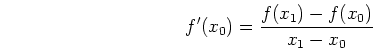Next: Newton-Raphson Method (Multi-Variate)
Up: Appendix
Previous: Functions of random variables
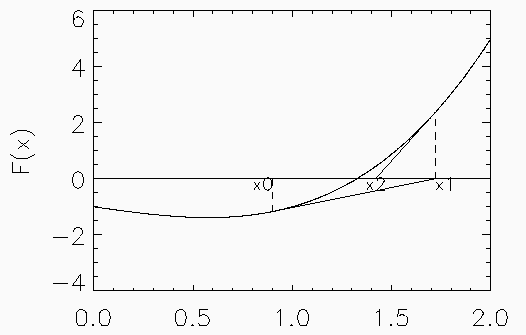
To solve an algebraic equation 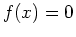 , select a random initial guess
, select a random initial guess 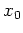 and follow the iteration:
and follow the iteration:
This Newton-Raphson formula can be derived below. The equation of the tangent
of 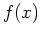 at
at 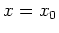 is
is
If we let 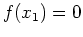 , i.e.,
, i.e., 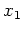 is the zero crossing of the tangent, we get
is the zero crossing of the tangent, we get
which is closer to the desired solution than 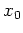 . Repeating the process we
will get
. Repeating the process we
will get
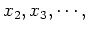 which approach the actual solution.
which approach the actual solution.
Ruye Wang
2018-03-26
![]() , select a random initial guess
, select a random initial guess ![]() and follow the iteration:
and follow the iteration: