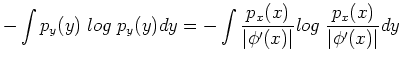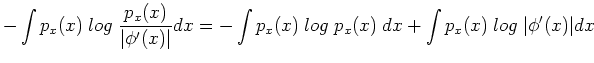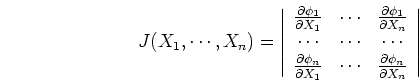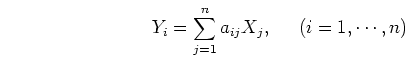Next: Newton-Raphson Method (Uni-Variate)
Up: Appendix
Previous: Mutual information
Assume 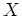 is a random variable with distribution
is a random variable with distribution 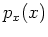 , then its function
, then its function
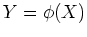 is also a random variable. We have
is also a random variable. We have
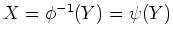 and
and 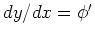 and
and
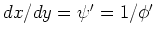 .
.
- Distribution
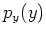 of
of 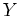 is related to distribution
is related to distribution 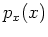 of
of 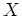 :
:
- If
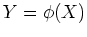 monotonically increases (
monotonically increases (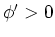 and
and 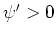 ), then
), then
- If
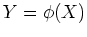 monotonically decreases (
monotonically decreases (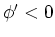 and
and 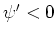 ), then
), then
In general, we have
where 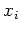 are solutions for equation
are solutions for equation 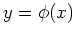 .
.
- Entropy
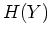 of
of 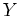 is related to entropy
is related to entropy 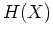 of
of
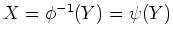 :
:
If the inverse function
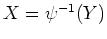 is not unique, than
is not unique, than
This result can be generalized to multi-variables. If
then
where
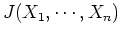 is the Jacobian of the above transformation:
is the Jacobian of the above transformation:
In particular, if the functions are linear
then
where 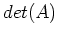 is the determinant of the transform matrix
is the determinant of the transform matrix
![$A=[a_{ij}]_{n\times n}$](img203.png) . Again, the equation holds if the transform is unique.
. Again, the equation holds if the transform is unique.



Next: Newton-Raphson Method (Uni-Variate)
Up: Appendix
Previous: Mutual information
Ruye Wang
2018-03-26
![]() is a random variable with distribution
is a random variable with distribution ![]() , then its function
, then its function
![]() is also a random variable. We have
is also a random variable. We have
![]() and
and ![]() and
and
![]() .
.