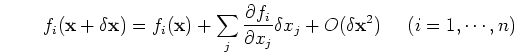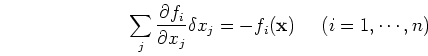Next: About this document ...
Up: Appendix
Previous: Newton-Raphson Method (Uni-Variate)
The above method can be generalized to multi-variate case to solve n simultaneous
algebraic equations
where
![${\mathbf x}=[x_1,\cdots,x_n]^T$](img81.png) is an n-dimensional vector. This equation
system can be more concisely represented in vector form as
is an n-dimensional vector. This equation
system can be more concisely represented in vector form as
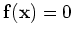 . The Newton-Raphson formula for multi-variate
problem is
. The Newton-Raphson formula for multi-variate
problem is
where
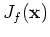 is the Jacobian of function
is the Jacobian of function
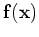 :
:
To derive this iteration, consider Taylor series
We ignore the terms of
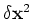 and higher and let
and higher and let
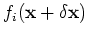 be zero (i.e.,
be zero (i.e.,
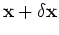 is the zero-crossing of the tangent), and get
is the zero-crossing of the tangent), and get
Solving this linear equation system for 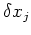 , we get
, we get
and the Newton-Raphson formula:
Ruye Wang
2018-03-26
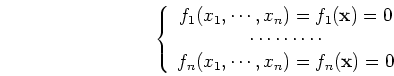
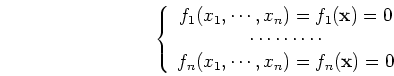
![\begin{displaymath}J_f( {\mathbf x})=\left[ \begin{array}{ccc}
\frac{\partial f...
...dots & \frac{\partial f_n}{\partial x_n}
\end{array} \right] \end{displaymath}](img219.png)