


Next: Two-Dimensional Fourier Transform (2DFT)
Up: fourier
Previous: Fast Fourier Transform (FFT)
Recall the symmetry properties of the DFT. The DFT of
![$x[m]=x_r[m]+jx_i[m]$](img166.png) is defined as
is defined as
where ![$X_r[n]$](img77.png) and
and ![$X_i[n]$](img78.png) are two real functions for the real and imaginary
parts of the spectrum, respectively. Consider the following two cases:
are two real functions for the real and imaginary
parts of the spectrum, respectively. Consider the following two cases:
- If
![$x[m]=x_r[m]$](img172.png) is real, i.e.,
is real, i.e., ![$x_i[m]=0$](img173.png) , then we have
, then we have
or
- If
![$x[m]=j x_i[m]$](img175.png) is imaginary, i.e.,
is imaginary, i.e., ![$x_r[m]=0$](img176.png) , then we have
, then we have
or
We note that half of the computation for the DFT of a real-valued signal ![$x[m]$](img8.png) is wasted, because
is wasted, because
- in the time domain, the imaginary components are all zero carrying no
information.
- in the frequency domain, due to the symmetry (even or odd), half of the
spectrum is redundant also carrying no independent information.
This waste of computation can be avoided by the following algorithm by which
the DFTs of two real signals can be obtained by only one DFT.
We first note that an arbitrary function 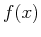 can be decomposed into the
even and odd components
can be decomposed into the
even and odd components 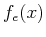 and
and 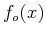 :
:
and
Now we can show how to obtain the DFT spectra
![$X_1[n]={\cal F}[x_1[m]]$](img184.png) and
and
![$X_2[n]={\cal F}[x_2[m]]$](img185.png) of two real functions
of two real functions ![$x_1[m]$](img186.png) and
and ![$x_2[m]$](img187.png) by
carrying out only one DFT.
by
carrying out only one DFT.
- Define a complex function
![$x[m]$](img8.png) by the two real functions:
by the two real functions:
Notice here that we impose 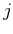 on
on ![$x_2[m]$](img187.png) to make it imaginary.
to make it imaginary.
- Obtain the DFT of
![$x[m]$](img8.png)
- Separate
![$X[n]={\cal F}[x[m]]$](img191.png) into
into
![$X_1[n]={\cal F}[x_1[m]]$](img184.png) and
and
![$X_2[n]={\cal F}[x_2[m]]$](img185.png) , based on the symmetry properties discussed previously.
Note that
, based on the symmetry properties discussed previously.
Note that ![$X[-n]=X[N-n]$](img198.png) because
because ![$X[n]$](img19.png) is a periodic function.
is a periodic function.



Next: Two-Dimensional Fourier Transform (2DFT)
Up: fourier
Previous: Fast Fourier Transform (FFT)
Ruye Wang
2015-11-12
![]() is defined as
is defined as
![$\displaystyle \sum_{m=0}^{N-1} x[m]e^{-j2\pi mn/N}=\sum_{m=0}^{N-1} [x_r[m]+jx_i[m]]\;
[\cos(2\pi mn/N)-j\;sin(2\pi mn/N)]$](img168.png)
![$\displaystyle \sum_{m=0}^{N-1} \left[x_r[m]\cos(\frac{2\pi mn}{N})+x_i[m]\sin\left(\frac{2\pi mn}{N}\right)\right]$](img169.png)
![$\displaystyle j\sum_{m=0}^{N-1} \left[x_i[m]\cos(\frac{2\pi mn}{N})-x_r[m]\sin\left(\frac{2\pi mn}{N}\right)\right]$](img171.png)
![\begin{displaymath}\left\{ \begin{array}{c} X_r[-n]=X_r[n] X_i[-n]=-X_i[n] \end{array} \right.
\end{displaymath}](img174.png)
![\begin{displaymath}\left\{ \begin{array}{c} X_r[-n]=-X_r[n] X_i[-n]=X_i[n] \end{array} \right.
\end{displaymath}](img177.png)
![]() is wasted, because
is wasted, because
![]() can be decomposed into the
even and odd components
can be decomposed into the
even and odd components ![]() and
and ![]() :
:
![]() and
and
![]() of two real functions
of two real functions ![]() and
and ![]() by
carrying out only one DFT.
by
carrying out only one DFT.