


Next: Fourier Transform 2 Real
Up: fourier
Previous: An Example
The N-point DFT of time samples
![$x[0], x[1], \cdots, x[N-1]$](img140.png) is defined as
(ignoring the coefficient
is defined as
(ignoring the coefficient 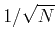 for now):
for now):
where we have defined
It is easy to show that 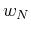 has the following properties:
has the following properties:
-
-
-
Let 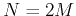 , the above DFT can be written as
, the above DFT can be written as
The first summation has all 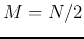 even terms and the second all
even terms and the second all
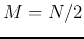 odd ones. Due to the 2nd property of
odd ones. Due to the 2nd property of 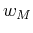 , the above can be
rewritten as
, the above can be
rewritten as
![\begin{displaymath}
X[n]=\sum_{m=0}^{M-1}x[2m]w_{M}^{mn}+\sum_{m=0}^{M-1}x[2m+1...
...n}[n]+X_{odd}[n] w_{2M}^n,\;\;\;\;\;\;\;\;\;\;(n=0,\cdots,M-1)
\end{displaymath}](img151.png) |
(1) |
where
are two M-point DFTs, where
Note that the index
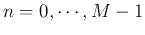 for these two M-point DFTs only
covers the first half of the range
for these two M-point DFTs only
covers the first half of the range
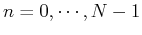 for the original
N-point DFT. However, the second half can be easily obtained by replacing
for the original
N-point DFT. However, the second half can be easily obtained by replacing
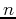 in Eq. (1) with
in Eq. (1) with 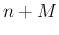 :
:
The last equation is due to the 3rd property of 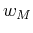 . Also, due to
the first property of
. Also, due to
the first property of 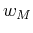 , we have
, we have
and
Now the second half of the N-point DFT can be obtained as
![\begin{displaymath}
X[n+M]=X_{even}[n]-X_{odd}[n] w_{2M}^n,\;\;\;\;\;\;\;\;\;\;(n=0,\cdots,M-1)
\end{displaymath}](img163.png) |
(2) |
The N-point DFT can now be obtained from Eqs. (1), (2), once ![$X_{ever}[n]$](img164.png) and
and ![$X_{odd}[n]$](img165.png) are available. However, as
are available. However, as ![$X_{ever}[n]$](img164.png) and
and ![$X_{odd}[n]$](img165.png) are
two N/2-point DFTs, they each can also be obtained by two N/4-point DFTs.
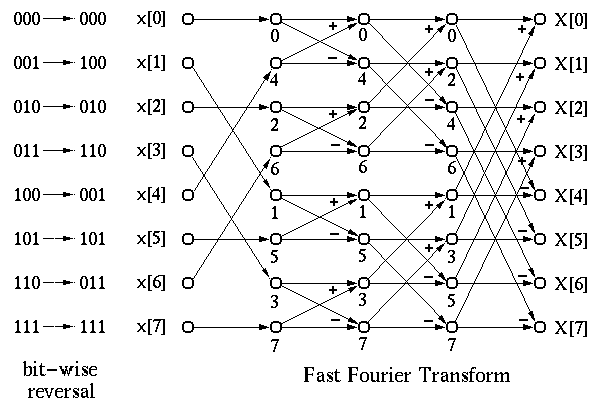
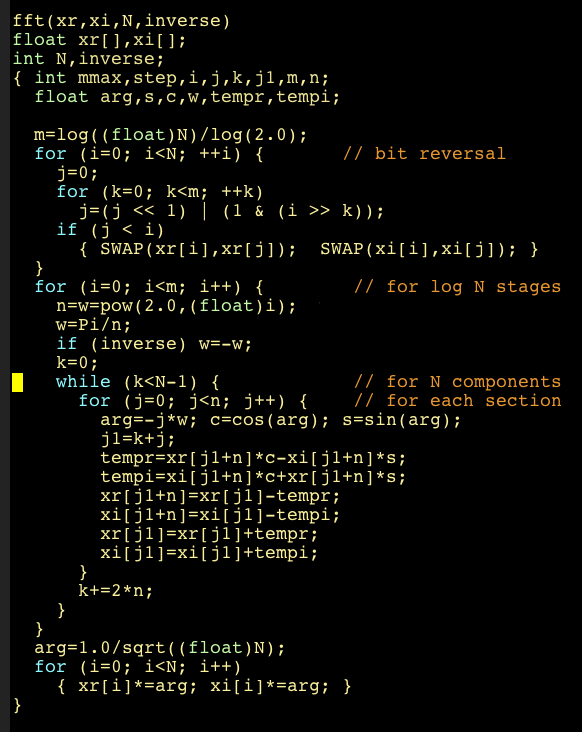
This process can be carried out recursively until finally only 1-point DFTs
are needed, which are just the time samples themselves. Therefore, the
operations of an N-point DFT can be symbolically represented by the following
diagram. The complexity is therefore reduced from
are
two N/2-point DFTs, they each can also be obtained by two N/4-point DFTs.
This process can be carried out recursively until finally only 1-point DFTs
are needed, which are just the time samples themselves. Therefore, the
operations of an N-point DFT can be symbolically represented by the following
diagram. The complexity is therefore reduced from 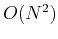 to
to
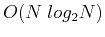 .
.



Next: Fourier Transform 2 Real
Up: fourier
Previous: An Example
Ruye Wang
2015-11-12
![]() is defined as
(ignoring the coefficient
is defined as
(ignoring the coefficient ![]() for now):
for now):
![\begin{displaymath}X[n]=\sum_{m=0}^{N-1} x[m]e^{-j2\pi mn/N}=\sum_{m=0}^{N-1}x[m]w_N^{mn}
\;\;\;\;\;\;\;\;\;\;(n=0, 1, \cdots, N-1) \end{displaymath}](img141.png)
![\begin{displaymath}X[n]=\sum_{m=0}^{N-1} x[m]w_{N}^{mn}
=\sum_{m=0}^{M-1} x[2m]w_{2M}^{2mn}+\sum_{m=0}^{M-1} x[2m+1]w_{2M}^{(2m+1)n} \end{displaymath}](img148.png)
![\begin{displaymath}
X[n]=\sum_{m=0}^{M-1}x[2m]w_{M}^{mn}+\sum_{m=0}^{M-1}x[2m+1...
...n}[n]+X_{odd}[n] w_{2M}^n,\;\;\;\;\;\;\;\;\;\;(n=0,\cdots,M-1)
\end{displaymath}](img151.png)
![\begin{displaymath}X_{even}[n]\stackrel{\triangle}{=}\sum_{m=0}^{M-1} x[2m]w_{M}...
...d}[n]\stackrel{\triangle}{=}\sum_{m=0}^{M-1} x[2m+1]w_{M}^{mn} \end{displaymath}](img152.png)
![\begin{displaymath}X_{even}[n+M]=\sum_{m=0}^{M-1} x[2m]w_{M}^{m(n+M)}
=\sum_{m=0}^{M-1} x[2m]w_{M}^{mn}=X_{even}[n]
\end{displaymath}](img161.png)
![\begin{displaymath}
X_{odd}[n+M]=\sum_{m=0}^{M-1} x[2m+1]w_{M}^{m(n+M)}
=\sum_{m=0}^{M-1} x[2m+1]w_{M}^{mn}=X_{odd}[n]
\end{displaymath}](img162.png)
![]() and
and ![]() are available. However, as
are available. However, as ![]() and
and ![]() are
two N/2-point DFTs, they each can also be obtained by two N/4-point DFTs.
This process can be carried out recursively until finally only 1-point DFTs
are needed, which are just the time samples themselves. Therefore, the
operations of an N-point DFT can be symbolically represented by the following
diagram. The complexity is therefore reduced from
are
two N/2-point DFTs, they each can also be obtained by two N/4-point DFTs.
This process can be carried out recursively until finally only 1-point DFTs
are needed, which are just the time samples themselves. Therefore, the
operations of an N-point DFT can be symbolically represented by the following
diagram. The complexity is therefore reduced from ![]() to
to
![]() .
.

