


Next: Fast Fourier Transform (FFT)
Up: fourier
Previous: Matrix form of the
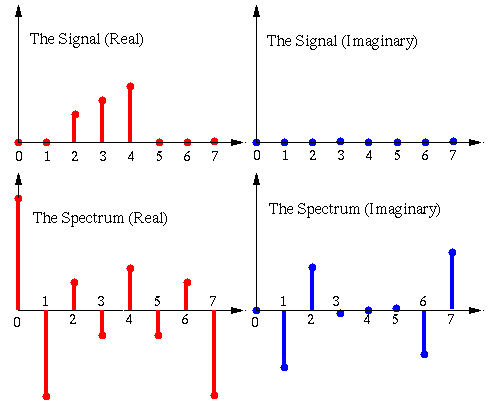
Consider a discrete signal ![$x[n]$](img6.png) of
of 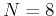 complex components:
complex components:
Note that Fourier transform is a complex transform. In general, the product
of two complex numbers 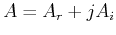 and
and 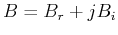 is also complex:
is also complex:
The foreword discrete Fourier transform is:
or
The inverse transform is:
or
These transforms can be expressed in matrix forms. For example, the forward
transform is:
For this specific example of 8-point DFT, we have
and
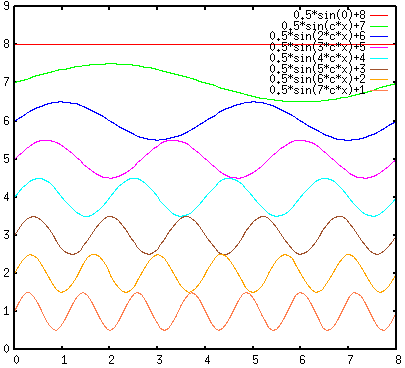
If the signal ![$x[m]$](img8.png) is real, then its spectrum
is real, then its spectrum ![$X[n]$](img19.png) has the following properties:
has the following properties:
- The real part of
![$X[0]$](img70.png) is the average or DC component
of the signal, the imaginary part of
is the average or DC component
of the signal, the imaginary part of ![$X[0]$](img70.png) is zero;
is zero;
- The real part of
![$x[N/2]$](img133.png) is the difference between the even components
and odd components, the imaginary part of
is the difference between the even components
and odd components, the imaginary part of ![$X[N/2]$](img134.png) is zero:
is zero:
- When
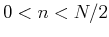 , the real part of
, the real part of ![$X[n]$](img19.png) is even symmetric and the
imaginary part of
is even symmetric and the
imaginary part of ![$X[n]$](img19.png) is odd symmetric:
is odd symmetric:



Next: Fast Fourier Transform (FFT)
Up: fourier
Previous: Matrix form of the
Ruye Wang
2015-11-12
![]() of
of ![]() complex components:
complex components:
![\begin{displaymath}{\bf x}=\left[
\begin{array}{c} x[0] x[1] x[2] x[3] ...
...3,0) (4,0) (0,0) (0,0) (0,0)
\end{tabular} \right] \end{displaymath}](img120.png)
![]() and
and ![]() is also complex:
is also complex:
![\begin{displaymath}X[n]= X_r[n]+jX_i[n]=\sum_{m=0}^{N-1} x[m] e^{-j2\pi m n/N}
...
...=0}^{N-1} (x_r[m]+jx_i[m]) (cos(2\pi m n/N)-j\;sin(2\pi mn/N)) \end{displaymath}](img124.png)
![\begin{displaymath}\left\{ \begin{array}{l}
X_r[n]=\sum_{m=0}^{N-1} x_r[m]cos(2...
..._i[m]cos(2\pi mn/N)-x_r[m]sin(2\pi m n/N)
\end{array} \right. \end{displaymath}](img125.png)
![\begin{displaymath}x[m]=x_r[m]+jx_i[m]=\frac{1}{N}\sum_{n=0}^{N-1} X[n] e^{j2\pi m n/N} \end{displaymath}](img126.png)
![\begin{displaymath}\left\{ \begin{array}{l}
x_r[m]=\sum_{n=0}^{N-1} X_r[n]cos(2...
..._i[n]cos(2\pi mn/N)+X_r[n]sin(2\pi m n/N)
\end{array} \right. \end{displaymath}](img127.png)
![\begin{displaymath}\left[
\begin{array}{c} X[0] X[1] X[2] X[3] X[4] ...
...] x[3] x[4] x[5] x[6] x[7]
\end{array} \right] \end{displaymath}](img128.png)
![\begin{displaymath}\left[ \begin{tabular}{r}
(9.0,0.0) (-6.1,-4.1) (2.0,...
...,0) (4,0) (0,0) (0,0) (0,0)
\end{tabular} \right]
\end{displaymath}](img130.png)


![]() is real, then its spectrum
is real, then its spectrum ![]() has the following properties:
has the following properties:
![\begin{displaymath}Re\{X[0]\}=\frac{1}{N} \sum_{m=0}^{N-1}x[m] cos(2\pi m 0/N)
=\frac{1}{N}\sum_{m=0}^{N-1} x[m] \end{displaymath}](img131.png)
![\begin{displaymath}Im\{X[0]\}=-\frac{1}{N} \sum_{m=0}^{N-1} x[m] sin(2\pi m 0/N)=0 \end{displaymath}](img132.png)
![\begin{displaymath}Re\{X[N/2]\}=\frac{1}{N} \sum_{m=0}^{N-1}x[m] cos(2\pi m N/2N)=
\frac{1}{N} \sum_{m=0}^{N-1}x[m] (-1)^m \end{displaymath}](img135.png)
![\begin{displaymath}Im\{X[N/2]\}=-\frac{1}{N} \sum_{m=0}^{N-1}x[m] sin(2\pi m N/2N)=0 \end{displaymath}](img136.png)
![\begin{displaymath}Re\{X[N-n]\}=\frac{1}{N} \sum_{m=0}^{N-1}x[m] cos(2\pi m (N-n...
...
=\frac{1}{N} \sum_{m=0}^{N-1}x[m] cos(2\pi m n/N)=Re\{X[n]\} \end{displaymath}](img138.png)
![\begin{displaymath}
Im\{X[N-n]\} = -\frac{1}{N} \sum_{m=0}^{N-1}x[m] sin(2\pi (N...
...\frac{1}{N} \sum_{m=0}^{N-1}x[m] sin(2\pi n m /N)=-Im\{X[n]\}
\end{displaymath}](img139.png)
