


Next: An Example
Up: fourier
Previous: The function and orthogonal
The forward and inverse DFT can be written as:
where we have defined
and 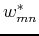 is its complex conjugate of
is its complex conjugate of 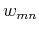 . We can further define an
. We can further define an
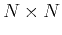 square matrix
square matrix
where 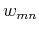 is the element in the mth row and nth column of
is the element in the mth row and nth column of 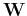 ,
and
,
and
![${\bf w}_n=[w_{0n},\cdots,w_{(N-1)n}]^T$](img104.png) is the nth column vector of
is the nth column vector of
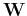 . As
. As 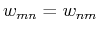 ,
, 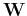 is symmetric
is symmetric
Also, note that the columns (or rows) of 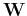 are orthogonal:
are orthogonal:
as
Therefore 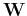 is a unitary matrix, as well and symmetric:
is a unitary matrix, as well and symmetric:
We further represent the discrete signal ![$x[m]$](img8.png) and its DFT spectrum
and its DFT spectrum ![$X[n]$](img19.png) as two N-D vectors:
as two N-D vectors:
then the DFT can be written more conveniently as a matrix-vector multiplication:
and
It is obvious that the computational complexity of this 1-D DFT takes is 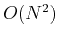 ,
which, as we will see later, can be reduced to
,
which, as we will see later, can be reduced to
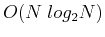 by Fast Fourier
Transform (FFT) algorithms.
by Fast Fourier
Transform (FFT) algorithms.
See additional geometric explanation
of unitary/orthogonal transform.



Next: An Example
Up: fourier
Previous: The function and orthogonal
Ruye Wang
2015-11-12
![\begin{displaymath}X[n]=\frac{1}{\sqrt{N}}\sum_{m=0}^{N-1} x[m]e^{-mn j2\pi/N}
...
...0}^{N-1} X[n]e^{mn j2\pi/N}
=\sum_{n=0}^{N-1} w_N^{-mn} X[n] \end{displaymath}](img32.png)
![\begin{displaymath}X[n]=\frac{1}{\sqrt{N}}\sum_{m=0}^{N-1} x[m]e^{-mn j2\pi/N}
...
...0}^{N-1} X[n]e^{mn j2\pi/N}
=\sum_{n=0}^{N-1} w_N^{-mn} X[n] \end{displaymath}](img32.png)
![\begin{displaymath}
{\bf W}=\left[{\bf w}_0,\cdots,{\bf w}_{N-1}\right]
=\left...
... . & w_{mn} & . \\
. & . & . \end{array} \right]_{N\times N}
\end{displaymath}](img102.png)
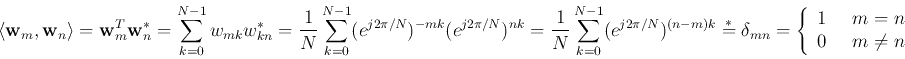
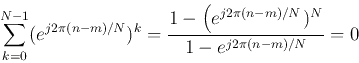
![\begin{displaymath}{\bf X}\stackrel{\triangle}{=}
\left[ \begin{array}{c} X[0] ...
...y}{c} x[0] . . x[N-1] \end{array}
\right]_{N\times 1}
\end{displaymath}](img114.png)
![\begin{displaymath}{\bf X}=\left[ \begin{array}{c} X[0] . . X[N-1] \end{a...
...{c} x[0] . . x[N-1] \end{array} \right]
={\bf W}{\bf x}
\end{displaymath}](img115.png)
![\begin{displaymath}{\bf x}=\left[ \begin{array}{c} x[0] . . x[N-1] \end{a...
...1] \end{array} \right]
={\bf W}^*{\bf X} ={\bf W}^{-1}{\bf X}
\end{displaymath}](img116.png)