


Next: Perfect Reconstruction Filters
Up: filterbank
Previous: Preparation: the Z-Transform
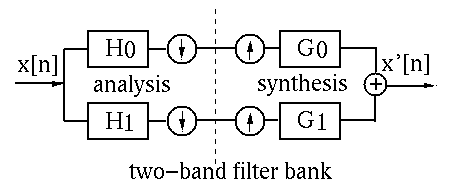
Consider a two-channel filter bank for 1D discrete signal ![$x[n]$](img1.png) as shown.
The idea is to separate the signal in frequency domain into two subbands
(e.g., high-band and low-band) so that each band can be down-sampled for
feature extraction, compression, and transmission and then up-sampled and
combined for recontruction of the original signal. Perfect reconstruction
as shown.
The idea is to separate the signal in frequency domain into two subbands
(e.g., high-band and low-band) so that each band can be down-sampled for
feature extraction, compression, and transmission and then up-sampled and
combined for recontruction of the original signal. Perfect reconstruction
![$x'[n]=x[n]$](img38.png) is possible if no information is lost during compression and
transmision.
is possible if no information is lost during compression and
transmision.
Applying the down and up sampling expressions to the subband system, we have
For perfect reconstruction, the output signal must be identical to the
original signal ![$x[n]=x'[n]$](img42.png) or
or 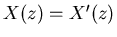 , i.e.,
, i.e.,
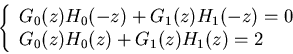 |
(1) |
which can be written in matrix form:
where
Solving this for 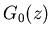 and
and 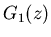 , we get:
, we get:
where
is the determinant of matrix 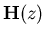 . From the above, we get
. From the above, we get
Replacing 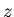 by
by 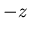 in the second equation above, we get
in the second equation above, we get
From the above two equations we can also get
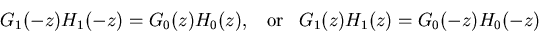 |
(2) |
Substituting Equaitons (2) into Equatioon (1), we get
Due to the following Z-transform: property
and convolution theorem, the time domain expression of the above equation is
The two terms on the left side of the equation cancel each other whenever
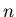 is odd, and the summation only has the even terms:
is odd, and the summation only has the even terms:
where
![$(a[n],b[n])=\sum_n a[n]^* b[n]$](img64.png) is the inner product of the two signals
is the inner product of the two signals
![$a[n]$](img65.png) and
and ![$b[n]$](img66.png) .
.
In addition to this relation between 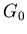 and
and 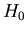 , from Eqautions (1)
and (2), we can also get three additional relations for
, from Eqautions (1)
and (2), we can also get three additional relations for 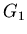 and
and 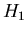 ,
,
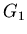 and
and 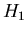 ,
, 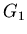 and
and 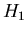 . These four relations can be summarized as:
. These four relations can be summarized as:
and equaivalently in time domain:
These four relations can be further summarized as
Filter banks satisfying this condition are called biorthogonal.



Next: Perfect Reconstruction Filters
Up: filterbank
Previous: Preparation: the Z-Transform
Ruye Wang
2007-10-01
![]() as shown.
The idea is to separate the signal in frequency domain into two subbands
(e.g., high-band and low-band) so that each band can be down-sampled for
feature extraction, compression, and transmission and then up-sampled and
combined for recontruction of the original signal. Perfect reconstruction
as shown.
The idea is to separate the signal in frequency domain into two subbands
(e.g., high-band and low-band) so that each band can be down-sampled for
feature extraction, compression, and transmission and then up-sampled and
combined for recontruction of the original signal. Perfect reconstruction
![]() is possible if no information is lost during compression and
transmision.
is possible if no information is lost during compression and
transmision.

![$\displaystyle \frac{1}{2}G_0(z)[H_0(z)X(z)+H_0(-z)X(-z)]
+\frac{1}{2}G_1(z)[H_1(z)X(z)+H_1(-z)X(-z)]$](img40.png)
![$\displaystyle \frac{1}{2}[G_0(z)H_0(z)+G_1(z)H_1(z)]X(z)
+\frac{1}{2}[G_0(z)H_0(-z)+G_1(z)H_1(-z)]X(-z)$](img41.png)
![]() or
or ![]() , i.e.,
, i.e.,
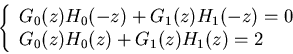
![\begin{displaymath}
\left[ \begin{array}{rr} H_0(-z) & H_1(-z) H_0(z) & H_1(z...
...} \right]
=\left[ \begin{array}{r} 0 2 \end{array} \right]
\end{displaymath}](img45.png)
![\begin{displaymath}
{\bf H}(z)=\left[ \begin{array}{rr} H_0(-z) & H_1(-z) H_0(z) & H_1(z) \end{array} \right]
\end{displaymath}](img46.png)
![$\displaystyle \left[ \begin{array}{r} G_0(z) G_1(z) \end{array} \right]$](img49.png)
![$\displaystyle {\bf H}(z)^{-1}\left[ \begin{array}{r} 0 2 \end{array} \right...
...H_0(-z)
\end{array} \right] \left[ \begin{array}{r} 0 2 \end{array} \right]$](img50.png)
![$\displaystyle \frac{2}{det{\bf H}(z)}\;\left[ \begin{array}{r} -H_1(-z) H_0...
...t{\bf H}(-z)}\;\left[ \begin{array}{r} H_1(-z) -H_0(-z) \end{array} \right]$](img51.png)
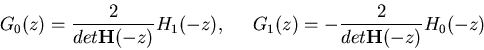
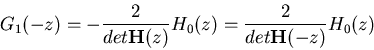
![]() and
and ![]() , from Eqautions (1)
and (2), we can also get three additional relations for
, from Eqautions (1)
and (2), we can also get three additional relations for ![]() and
and ![]() ,
,
![]() and
and ![]() ,
, ![]() and
and ![]() . These four relations can be summarized as:
. These four relations can be summarized as:
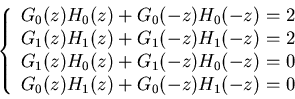
![\begin{displaymath}\left\{ \begin{array}{l}
\sum_k g_0[k]h_0[2n-k]=(g_0[n],h_0[...
...sum_k g_0[k]h_1[2n-k]=(g_0[n],h_1[2n-k])=0 \end{array} \right. \end{displaymath}](img72.png)