


Next: About this document ...
Up: filterbank
Previous: Subband Coding
From above we know that the output ![$x'[n]$](img32.png) of a 2-channel filter bank can be
a perfect reconstruction of the input
of a 2-channel filter bank can be
a perfect reconstruction of the input ![$x[n]$](img1.png) if the following conditions are
satisfied (equation (1) in previous section):
if the following conditions are
satisfied (equation (1) in previous section):
Note that the subsampling rate does not have to be above the Nyquest frequency
specified by the sampling theorem. Even if the signal is undersampled and alising
exists, the perfect reconstruction of the signalit is guaranteed due to the
upsampling and synthesis filters determined by the above equations.
As there are four function variables 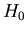 ,
, 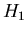 ,
, 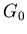 and
and 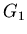 in the two
equations, there exist many possible designs for the filter banks. Here are three
particular ones:
in the two
equations, there exist many possible designs for the filter banks. Here are three
particular ones:
- Quadrature mirror filters (QMFs)
We let
both of the two equations above can be written in terms of 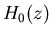 . The
first equation above becomes:
. The
first equation above becomes:
and the second equation becomes:
where 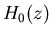 is so chosen that
is so chosen that
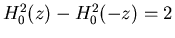 to satisfy the requirement
for perfect reconstruction.
to satisfy the requirement
for perfect reconstruction.
- Conjugate quadrature filters (CQFs)
We let
and both of the two equations above can be written in terms of 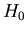 . The
first equation above becomes:
. The
first equation above becomes:
and the second equation becomes:
where 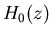 is so chosen that the second expression is 2 to satisfy the
requirement for perfect reconstruction.
is so chosen that the second expression is 2 to satisfy the
requirement for perfect reconstruction.
- Orthonormal (fast wavelet transform) filter
We let
and both of the two equations above can be written in terms of 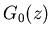 . The
first equation above becomes:
. The
first equation above becomes:
and the second equation becomes:
where 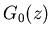 is so chosen that the second expression is 2 to satisfy the
requirement for perfect reconstruction. Note that
is so chosen that the second expression is 2 to satisfy the
requirement for perfect reconstruction. Note that
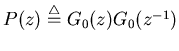 is the Z-transform of the
autocorrelation
is the Z-transform of the
autocorrelation
![$p[n]=\sum_m g_0[m]g_0[m+n]$](img92.png) , and the second equation becomes
, and the second equation becomes
Replacing 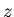 by
by 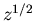 , we get
, we get
Consider the down sampled version of the function
![$g'_0[n]=g_0[2n]$](img96.png) , and its
autocorrelation
, and its
autocorrelation ![$p'[n]=p[2n]$](img97.png) . As in Z domain we have:
. As in Z domain we have:
in time domain we have
i.e., the down-sampled version of ![$g_0[n]$](img100.png) is orthonormal.
is orthonormal.
Example: There are different ways to design the FIR filter orthonormal
impulse response ![$g_0[n]$](img100.png) for the two-channel filter bank.
for the two-channel filter bank.
The conditions for perfect construction filters listed above can be
inverse Z-transformed to get:
i.e., 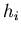 is the time-reversed version of
is the time-reversed version of 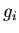 (
(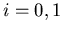 ), and
), and 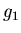 is
both time reversed and modulated version of
is
both time reversed and modulated version of 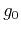 . Once
. Once 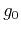 is determined,
the rest can all be determined.
is determined,
the rest can all be determined.



Next: About this document ...
Up: filterbank
Previous: Subband Coding
Ruye Wang
2007-10-01
![]() of a 2-channel filter bank can be
a perfect reconstruction of the input
of a 2-channel filter bank can be
a perfect reconstruction of the input ![]() if the following conditions are
satisfied (equation (1) in previous section):
if the following conditions are
satisfied (equation (1) in previous section):
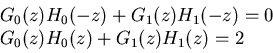
![]() ,
, ![]() ,
, ![]() and
and ![]() in the two
equations, there exist many possible designs for the filter banks. Here are three
particular ones:
in the two
equations, there exist many possible designs for the filter banks. Here are three
particular ones:
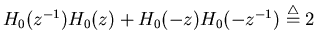
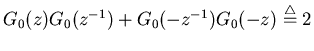
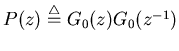 is the Z-transform of the
autocorrelation
is the Z-transform of the
autocorrelation
![]() for the two-channel filter bank.
for the two-channel filter bank.