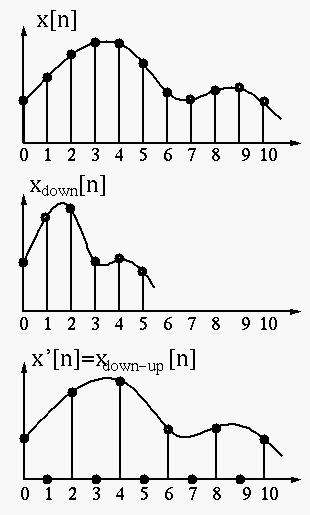Preparation: the Z-Transform

The Z-transform of a discrete signal $x[n]$ is defined as

$$X(z)={\cal Z}(x[n])=\sum_{n=-\infty}^\infty x[n] z^{-n}$$

In case you are not familiar with Z-transform, recall discrete Fourier transform:

$$X(j\omega)=\sum_{n=-\infty}^\infty x[n] e^{-j\omega n}$$

If we define $z=e^{j\omega}$, the discrete Fourier transform becomes Z-transform defined above.

• Convolution The convolution of two signals $x[n]$ and $y[n]$ is
  
  $$x*y=\sum_k x[n-k]y[k]=\sum_k x[k]y[n-k]$$
  
  
  and its z-transform is
  
  $${\cal Z}[x*y]=X(z)Y(z)$$
  
  

• Time reversal

  The z-transform of the time-reversed version $x[-n]$ of the signal is
  

  $$X_{reversal}(z)=\sum_{n=-\infty}^\infty x[-n] z^{-n} =\sum_{n=-\infty}^\infty x[n] (z^{-1})^{-n}=X(z^{-1})$$
  
  

• Time shift

  The z-transform of the time-shifted version $x[n-k]$ of the signal is
  

  $$X_{reversal}(z)=\sum_{n=-\infty}^\infty x[n-k] z^{-n} =\sum_{n'=-\infty}^\infty x[n'] z^{-n'-k}=z^{-k}X(z)$$
  
  
  where $n'=n-k$.

• Modulation

  Here modulation means every other sample of the signal is negated:
  

  $$x'[n]=(-1)^n x[n]$$
  
  
  and the z-transform is
  
  $$X'(z)=\sum_{n=-\infty}^\infty x[n](-1)^n z^{-n} =\sum_{n=-\infty}^\infty x[n] (-z)^{-n} =X(-z)$$
  
  

• Down-sampling:

  The z-transform of a down-sampled version of the signal $x_{down}[n]=x[2n]$ is
  

  $$X_{down}(z)=\sum_{n=-\infty}^\infty x[2n] z^{-n}$$
  
  
  Let $m=2n$, i.e., $n=m/2$, we get
  

  $$X_{down}(z) = \sum_{m=\cdots,-2,0,,2,\cdots} x[m] (z^{1/2})^{-m} =\frac{1}{2}[\... ...infty}^\infty x[m] (z^{1/2})^{-m}+\sum_{m=-\infty}^\infty x[m] (-z^{1/2})^{-m}]$$

  $$= \frac{1}{2}[X(z^{1/2})+X(-z^{1/2})]$$

  
  

  Example 0: The Z-transform of a modulated, time-reversed and shifted signal $(-1)^n x[k-n]$ is
  

  $${\cal Z}[(-1)^n x[k-n]]=\sum_{n=-\infty}^\infty (-1)^n x[k-n]z^{-n} =\sum_{n=-\infty}^\infty x[k-n](-z)^{-n}$$

  $$= \sum_{m=-\infty}^\infty x[m](-z)^{m-k} =(-z)^{-k} \sum_{m=-\infty}^\infty x[m](-z^{-1})^{-m}=(-z)^{-k}X(-z^{-1})$$

  
  
  where $m=k-n$.

• Up-sampling:

  The up-sampled version of a signal $x[n]$ is
  

  $$x_{up}[n]=\left\{ \begin{array}{ll} x[n/2] & n=0,2,4,\cdots \\ 0 & \mbox{otherwise} \end{array} \right.$$
  
  
  and its Z-transform is
  
  $$X_{up}(z)=\sum_{n=\cdots,-2,0,2,\cdots} x[n/2] z^{-n} =\sum_{m=\cdots,-1,0,1,\cdots} x[m] (z^2)^{-m}=X(z^2)$$
  
  
  where $m=n/2$.

Example 1: The autocorrelation of a signal $x[n]$

$$\sum_k x[k] x[k-n]$$

can be viewed as the convolution of $x[n]$ with its time reversed version. Therefore the z-transform of the autocorrelation is

$${\cal Z}[\sum_k x[k] x[k-n]]]=X(z)X(z^{-1})$$

Example 2:

When a signal $x[n]$ is first down-sampled and then up-sampled to become $x'[n]$, its z-transform becomes:

$$X'(z)=\frac{1}{2}[X(z)+X(-z)]$$

As

$$X(-z)=\sum_{n=-\infty}^\infty x[n] (-z)^{-n}=\sum_{n=-\infty}^\infty (-1)^n x[n] z^{-n}$$

the inverse z-transform of $X(-z)$ is

$${\cal Z}^{-1} X(-z)=(-1)^n x[n]$$

and

$$x'[n]={\cal Z}^{-1} X'(z)=\frac{1}{2}[{\cal Z}^{-1} X(z)+{\ca... ... & \mbox{even}\; n \\ 0 & \mbox{odd}\; n \end{array} \right.$$