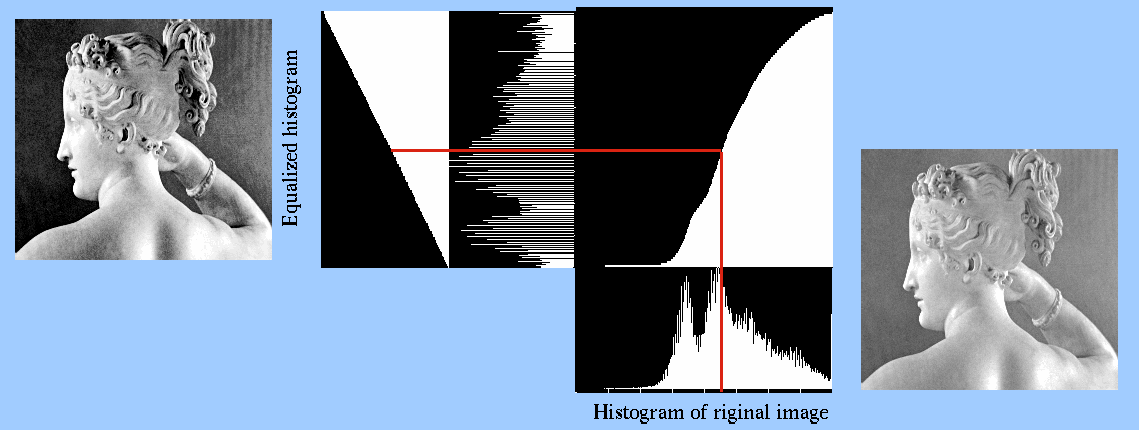
Next: Histogram Specification Up: contrastTransform Previous: Gray level mapping
To transform the gray levels of the image so that the histogram of the resulting image is equalized to become a constant:
![$\displaystyle h[i]=\frac{1}{L}=$](img36.svg) constant constant |
(6) |
The purposes:
We first assume the pixel values are continuous in the range
of 





 |
(7) |
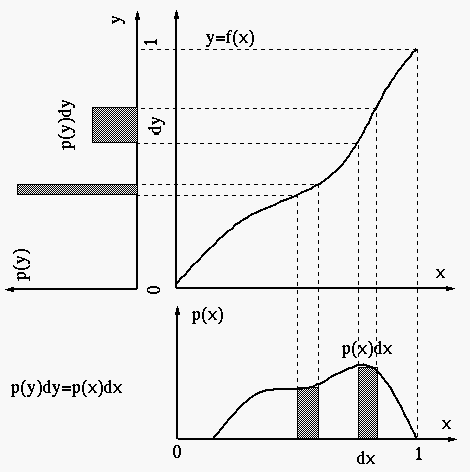
For the histogram of the output image to be equalized, it
needs to be constant 1, i.e., 
 |
(8) |
 or or |
(9) |
 for the histogram equalization:
for the histogram equalization:
 |
(10) |
 is the cumulative distribution of the gray
levels of the input image:
is the cumulative distribution of the gray
levels of the input image:
 |
(11) |
This histogram equalization mapping can be intuitively
understood by checking the following two cases while
both need to keep

 is low,
is low,  has a shallow slope, then
has a shallow slope, then
 is narrow and
is narrow and  is high;
is high;
 is high,
is high,  has a steep slope, then
has a steep slope, then
 is wide and
is wide and  is low.
is low.
 to low
to low  and low
and low
 to high
to high  , i.e., it tends to make
, i.e., it tends to make  a flat
curve, a uniform distribution.
a flat
curve, a uniform distribution.
For discrete gray levels, the gray level of the input 


![$\displaystyle y'[j]=H_x[j]\stackrel{\triangle}{=}\sum_{i=0}^j h_x[i]$](img55.svg) |
(12) |
![$h_x[i]$](img56.svg) and
and ![$H_x[j]$](img57.svg) are respectively the density and
cumulative histogram of the input image
are respectively the density and
cumulative histogram of the input image  :
:
![$\displaystyle h_x[i]=\frac{n_i}{\sum_{i=0}^{L-1} n_i}
=\frac{n_i}{N},\;\;\;\;\;\;\;
H_x[j]=\sum_{i=0}^j h_x[i],\;\;\;\;\;\;H_x[L-1]
=\sum_{i=0}^{L-1} h_x[i]=1$](img58.svg) |
(13) |
 is the number of pixels with gray level
is the number of pixels with gray level  , and
, and  is the total number of pixels.
is the total number of pixels.
The resulting function 


 |
(14) |
 |
(15) |
 is the floor of a real number
is the floor of a real number  (the
largest integer smaller than
(the
largest integer smaller than  ), and adding
), and adding  is for proper
rounding. Note that both conversions map
is for proper
rounding. Note that both conversions map
 to the highest
gray level
to the highest
gray level  , but the second conversion also maps
, but the second conversion also maps  to
0 to stretch the gray levels of the output image to occupy the
entire dynamic range
to
0 to stretch the gray levels of the output image to occupy the
entire dynamic range  ; i.e., the second method does
gray scale stretch as well as histogram equalization.
; i.e., the second method does
gray scale stretch as well as histogram equalization.
Example:
Assume the images have


 |
(16) |
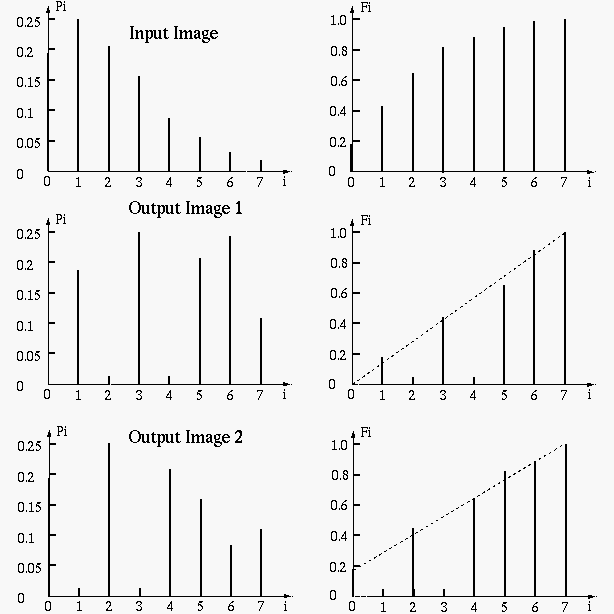
In the following example, the histogram of a given image is equalized. Although the resulting histogram may not look constant due to the discrete nature of the digital image, the cumulative histogram is an exact linear ramp indicating that the density histogram is indeed equalized. The density histogram is not guaranteed to be a constant because the pixels of the same gray level cannot be separated to satisfy a constant distribution.

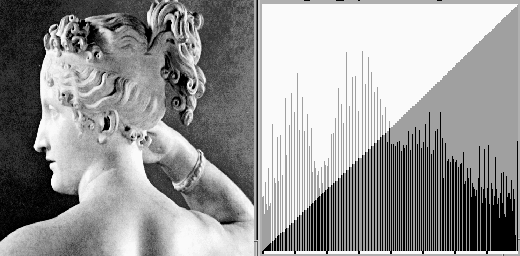
Build lookup table:
sum=0.0;
for (i=0; i<256; i++) {
sum=sum+h[i];
lookup[i]=sum*255;
}
Image Mapping:
for (m=0; m<M; m++)
for (n=0; n<N; n++)
y[m][n]=lookup[x[m][n]];
Example: