


Next: Maximization of Entropy
Up: Information Theory
Previous: Measurement of uncertainty and
A random experiment may have binary (e.g., rain or dry) or multiple outcomes.
For example, a dice has six possible outcomes with equal probability, or a pixel
in a digital image takes one of the 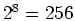 gray levels (0 255) with not
necessarily the same probability. In general, these multiple outcomes can be
considered as
gray levels (0 255) with not
necessarily the same probability. In general, these multiple outcomes can be
considered as 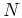 events
events  with corresponding probability
with corresponding probability  (
( ), which are
), which are
- complementary
where
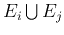 is the union (OR) of events
is the union (OR) of events  and
and  , and
, and
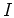 is a necessary event with
is a necessary event with  , so that
, so that
- mutually exclusive
where
 is the intersection (AND) of events
is the intersection (AND) of events  and
and  ,
and
,
and  is an impossible event with
is an impossible event with 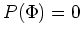 , so that
, so that
The uncertainty about the outcome of such a random experiment is the sum of the
uncertainty 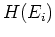 associated with each individual event
associated with each individual event  , weighted by
its probability
, weighted by
its probability 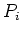 :
:
This is called the entropy which measures the uncertainty of the random
experiment. Once the result of the experiment is known, the uncertainty becomes
zero, i.e., the entropy is also the information associated with the experiment.
The specific logarithmic base is not essential. If the base is 2, the unit of
entropy is the bit; if the base is 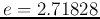 , the unit is nat (or nit).
, the unit is nat (or nit).
For example, the weather can have two complementary and mutually exclusive
possible outcomes: rain  with probability
with probability 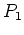 or dry
or dry 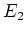 with
probability
with
probability 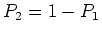 . The uncertainty of the weather is therefore the
sum of the uncertainty of a rainy weather and the uncertainty of a fine
weather weighted by their probabilities:
. The uncertainty of the weather is therefore the
sum of the uncertainty of a rainy weather and the uncertainty of a fine
weather weighted by their probabilities:
In particular, consider cases:
- If
 and
and 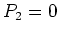 (or vice versa), we have the minimum
uncertainty zero (note that
(or vice versa), we have the minimum
uncertainty zero (note that
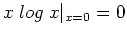 ):
):
- If
 ,
,  , the uncertainty is:
, the uncertainty is:
- If
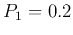 ,
, 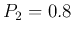 , the uncertainty is:
, the uncertainty is:
- If
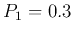 ,
, 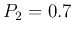 , the uncertainty is:
, the uncertainty is:
- If
 ,
, 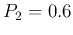 , the uncertainty is:
, the uncertainty is:
- If
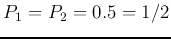 , we have the maximum uncertainty:
, we have the maximum uncertainty:



Next: Maximization of Entropy
Up: Information Theory
Previous: Measurement of uncertainty and
Ruye Wang
2021-03-28
![]() gray levels (0 255) with not
necessarily the same probability. In general, these multiple outcomes can be
considered as
gray levels (0 255) with not
necessarily the same probability. In general, these multiple outcomes can be
considered as ![]() events
events ![]() with corresponding probability
with corresponding probability ![]() (
(![]() ), which are
), which are


![]() associated with each individual event
associated with each individual event ![]() , weighted by
its probability
, weighted by
its probability ![]() :
:
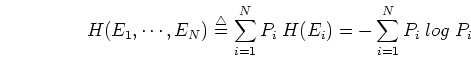
![]() with probability
with probability ![]() or dry
or dry ![]() with
probability
with
probability ![]() . The uncertainty of the weather is therefore the
sum of the uncertainty of a rainy weather and the uncertainty of a fine
weather weighted by their probabilities:
. The uncertainty of the weather is therefore the
sum of the uncertainty of a rainy weather and the uncertainty of a fine
weather weighted by their probabilities: