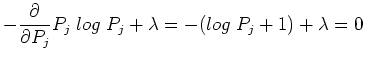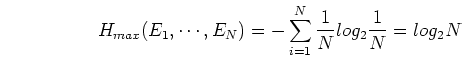Next: Image Compression with Huffman
Up: Information Theory
Previous: Entropy, uncertainty of random
Unlike a single event 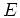 (e.g., rainy weather) whose uncertainty is not bounded
(when
(e.g., rainy weather) whose uncertainty is not bounded
(when
 ,
,
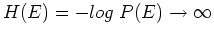 ), the uncertainty
of a random experiment with finite outcomes is bounded by a maximum entropy, which
can be obtained by finding
), the uncertainty
of a random experiment with finite outcomes is bounded by a maximum entropy, which
can be obtained by finding  (
(
 ) so that the entropy
) so that the entropy
is maximized with the constraint
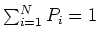 . This is a constrained
maximization problem which can be solved by Lagrange multiplier method:
. This is a constrained
maximization problem which can be solved by Lagrange multiplier method:
Solving this we get
indicating that all 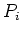 's must be the same. But as they also have to add up to 1,
we have
's must be the same. But as they also have to add up to 1,
we have
and the corresponding maximum entropy can be obtained as
This result that a random event with equally likely outcomes has maximum entropy
makes intuitive sense, as the uncertainty is always reduced if some outcomes are
more likely than others. In particular when  , we have
, we have 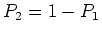 and the
entropy
and the
entropy
reaches maximum 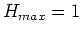 when the two outcomes are equally likely
when the two outcomes are equally likely 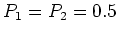 .
(This may be why a cow may starve to death when standing in between of two equally
wonderful piles of hay.)
.
(This may be why a cow may starve to death when standing in between of two equally
wonderful piles of hay.)




Next: Image Compression with Huffman
Up: Information Theory
Previous: Entropy, uncertainty of random
Ruye Wang
2021-03-28
![]() (e.g., rainy weather) whose uncertainty is not bounded
(when
(e.g., rainy weather) whose uncertainty is not bounded
(when
![]() ,
,
![]() ), the uncertainty
of a random experiment with finite outcomes is bounded by a maximum entropy, which
can be obtained by finding
), the uncertainty
of a random experiment with finite outcomes is bounded by a maximum entropy, which
can be obtained by finding ![]() (
(
![]() ) so that the entropy
) so that the entropy

![$\displaystyle \frac{\partial}{\partial P_j} [-\sum_{i=1}^N P_i log \;P_i
+\lambda(\sum_{i=0}^NP_i-1)]=0$](img81.png)