


Next: Entropy, uncertainty of random
Up: Information Theory
Previous: Probability, uncertainty and information
In case of multiple events, such as 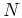 independent events
independent events 
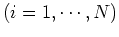 ,
the associated uncertainty
,
the associated uncertainty
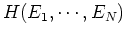 is related to the joint
probability of the occurrence of all of the events, which is the product of their
individual probabilities
is related to the joint
probability of the occurrence of all of the events, which is the product of their
individual probabilities 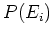 :
:
However it is desirable (and intuitively makes sense) for the total uncertainty
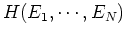 to be the sum of the individual uncertainties:
to be the sum of the individual uncertainties:
Summarizing the above, we see that the uncertainty  associated with an event
associated with an event
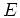 with probability
with probability  should satisfy these constraints:
should satisfy these constraints:
- More probable events have lower uncertainty, i.e.,
 is monotonically
related to
is monotonically
related to  ;
;
- Necessary event has no uncertainty, i.e.,
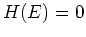 when
when  ;
;
 is additive in multi-event case where
is additive in multi-event case where  is multiplicative.
is multiplicative.
The uncertainty, also called surprise,  of an event
of an event 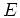 is therefore defined as:
is therefore defined as:
When  , e.g., the sun will rise tomorrow, the surprise is 0, when
, e.g., the sun will rise tomorrow, the surprise is 0, when
 , e.g., the sun will rise in the west, the surprise is
, e.g., the sun will rise in the west, the surprise is 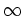 .
Also this definition obviously satisfies the first two constraints. In
multi-event case we have
.
Also this definition obviously satisfies the first two constraints. In
multi-event case we have
i.e., the uncertainties are additive as required by the third constraint.
Note that for an impossible event 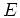 with
with  , the uncertainty
, the uncertainty
 . If you are told such an impossible event could
actually occur (
. If you are told such an impossible event could
actually occur (
 ) or did occur (
) or did occur (
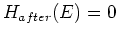 ),
infinite amount of information would be gained:
),
infinite amount of information would be gained:
So you will get no information if some one tells you the sun will rise tomorrow
morning (
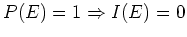 ), but you will get infinite amount of information
if someone tells you the sun will rise in the west (
), but you will get infinite amount of information
if someone tells you the sun will rise in the west (
 ).
).



Next: Entropy, uncertainty of random
Up: Information Theory
Previous: Probability, uncertainty and information
Ruye Wang
2021-03-28
![]() independent events
independent events ![]()
![]() ,
the associated uncertainty
,
the associated uncertainty
![]() is related to the joint
probability of the occurrence of all of the events, which is the product of their
individual probabilities
is related to the joint
probability of the occurrence of all of the events, which is the product of their
individual probabilities ![]() :
:
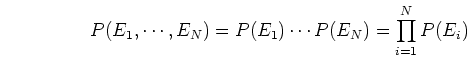

![]() associated with an event
associated with an event
![]() with probability
with probability ![]() should satisfy these constraints:
should satisfy these constraints:

![]() with
with ![]() , the uncertainty
, the uncertainty
![]() . If you are told such an impossible event could
actually occur (
. If you are told such an impossible event could
actually occur (
![]() ) or did occur (
) or did occur (
![]() ),
infinite amount of information would be gained:
),
infinite amount of information would be gained:
![]() ), but you will get infinite amount of information
if someone tells you the sun will rise in the west (
), but you will get infinite amount of information
if someone tells you the sun will rise in the west (
![]() ).
).