


Next: Performance Measurements
Up: classify
Previous: Distance Measurements
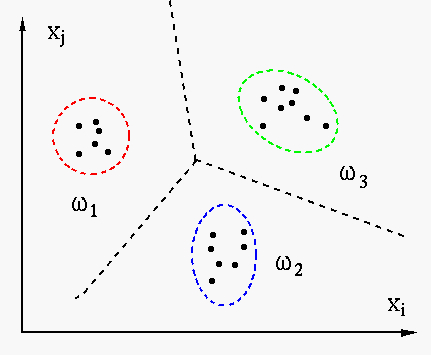
In feature selection, we need to evaluate how separable a set of classes are
in an M-dimensional feature space by some criteria.
- Total number of samples:
where 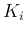 is the number of samples in class
is the number of samples in class 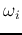
- Overall mean vector:
where 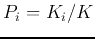 is the a priori probability of class
is the a priori probability of class 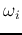
- Scatter matrix of class
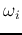 (same as the covariance matrix of
the class):
(same as the covariance matrix of
the class):
- Within-class scatter matrix:
- Between-class scatter matrix:
- Total scatter matrix:
We can show that
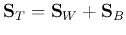 , i.e., the total scatteredness is the
sum of within-class scatteredness and between-class scatteredness.
, i.e., the total scatteredness is the
sum of within-class scatteredness and between-class scatteredness.
* Proof:
We can use the traces of these scatter matrices as some scalar criteria
to measure the separability between the classes:
and
We see that 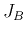 is the weighted average of the Euclidean distances between
is the weighted average of the Euclidean distances between
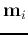 and
and 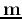 for all
for all 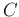 classes, and
classes, and 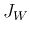 is the weighted average
of the Euclidean distances between
is the weighted average
of the Euclidean distances between 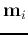 and
and 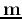 for all
for all 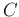 classes.
classes.
It is obviously desirable to maximize 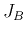 while at the same time also minimize
while at the same time also minimize
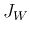 , so that the classes are maximally separated for the classification to be
most effectively carried out. We can therefore construct a new scalar criterion
to be used in feature selection
, so that the classes are maximally separated for the classification to be
most effectively carried out. We can therefore construct a new scalar criterion
to be used in feature selection
or, equivalently, due to the relationship
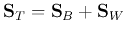 ,
,



Next: Performance Measurements
Up: classify
Previous: Distance Measurements
Ruye Wang
2016-11-30


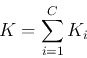
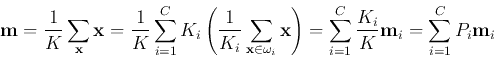
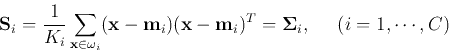
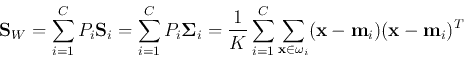
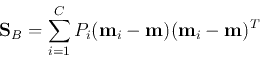
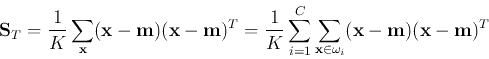
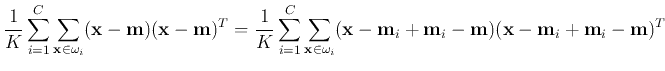
![$\displaystyle \frac{1}{K}\sum_{i=1}^C \sum_{{\bf x} \in \omega_i}
[({\bf x}-{\b...
...bf m}_i-{\bf m})({\bf x}-{\bf m}_i)^T+({\bf m}_i-{\bf m})({\bf m}_i-{\bf m})^T]$](img84.png)
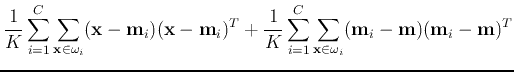
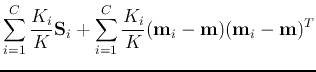
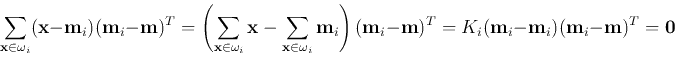
![$\displaystyle tr\;{\bf S}_B=tr\;\left[\sum_{i=1}^C P_i({\bf m}_i-{\bf m})({\bf m}_i-{\bf m})^T\right]$](img91.png)
![$\displaystyle \sum_{i=1}^C P_i\;tr\left[({\bf m}_i-{\bf m})({\bf m}_i-{\bf m})^T\right]
=\sum_{i=1}^C P_i\;\vert\vert{\bf m}_i-{\bf m}\vert\vert^2$](img92.png)
![$\displaystyle tr\;{\bf S}_W
=tr\left[\sum_{i=1}^C P_i \sum_{{\bf x}\in\omega_i}({\bf x}-{\bf m}_i)({\bf x}-{\bf m}_i)^T \right]$](img94.png)
![$\displaystyle \sum_{i=1}^C P_i \sum_{{\bf x}\in\omega_i}tr\left[({\bf x}-{\bf m}_i)({\bf x}-{\bf m}_i)^T \right]$](img95.png)
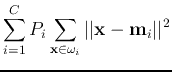
![]() while at the same time also minimize
while at the same time also minimize
![]() , so that the classes are maximally separated for the classification to be
most effectively carried out. We can therefore construct a new scalar criterion
to be used in feature selection
, so that the classes are maximally separated for the classification to be
most effectively carried out. We can therefore construct a new scalar criterion
to be used in feature selection