Performance Measurements

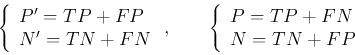
Consider a binary classifier that classifies each input pattern in a data set into two classes, either positive (P') or negative (N'), while the ground truth is either positive (P) or negative (N). The performance of the classifier can be represented in terms of these four possible classification results:

• True positive (TP): the result is positive (P') while the ground truth is also positive (P)
• False positive (FP): the result is positive (P') but the ground truth is negative (N)
• True negative (TN): the result is negative (N') while the ground truth is also negative (N)
• False negative (FN): the result is negative (N') but the ground truth is positive (P)

All such symbols can be also treated as the number of patterns that belong to each of the cases, and we have

$$\left\{\begin{array}{l} P'=TP+FP N'=TN+FN \end{array} \rig... ...\left\{\begin{array}{l} P=TP+FN N=TN+FP \end{array} \right.$$

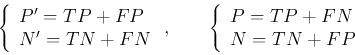
The four cases of the classification result can be represented by the following 2 by 2 confusion matrix (contingency table):

Based on these concepts, we can further define the following performance measurements (all in percentage between 0 and 1):

• Accuracy:
  
  $$ACC=\frac{TP+TN}{P+N}$$
  
  

• Error rate:
  
  $$ERR=\frac{FP+FN}{P+N}=1-ACC$$
  
  

• True positive rate (sensitivity):
  
  $$TPR=\frac{TP}{P}=\frac{TP}{TP+FN}$$
  
  

• True negative rate (specificity):
  
  $$TNR=\frac{TN}{N}=\frac{TN}{FP+TN}$$
  
  

• False positive rate:
  
  $$FPR=\frac{FP}{N}=\frac{FP}{FP+TN}=1-\frac{TN}{N}=1-TNR$$
  
  

• False negative rate:
  
  $$FNR=\frac{FN}{P}=\frac{FN}{TP+FN}=1-\frac{TP}{P}=1-TPR$$
  
  

An ideal classifier should have $100\%$ sensitivity ($TPR=1$) and $100\%$ specificity ($TNR=1$, or $FPR=0$)

The receiver operating characteristic (ROC) is the plot of TPR (sensitivity) versus FPR (1-specificity). The classification result in terms of the TPR and RPR corresponds to a point in the ROC plot. As the best (perfect) classification have $TPR=1$ and $TNR=1$ (i.e., $FPR=0$), it corresponds to the point at the top-left corner for 100% TPR and 0% FPR, while the worst corresponds to the lower-right corner for $TPR=0$ and $FPR=1$. A random guess (by 50% 50% chance) corresponds the diagonal of the plot. All points above/below the diagonal indicate better/worse results than a random guess. The ROC can be used to compare the performances of different classifiers.

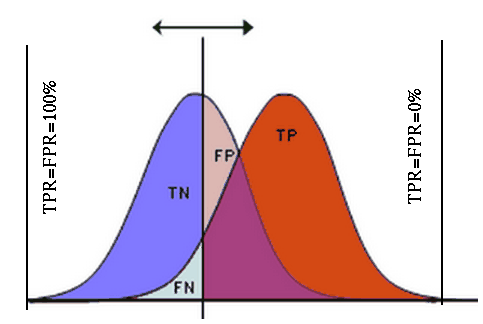
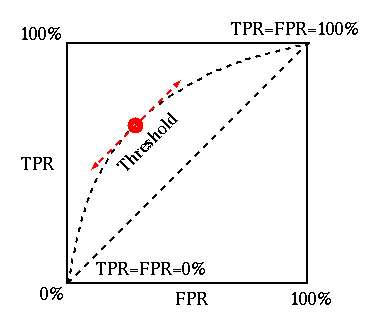
A classifier produces a value to indicate the likelihood of any given input to be either positive or negative. If this value is greater than pre-set thresholded $T$ (a parameter for the classifier), then the prediction is positive (P'), otherwise it is negative (N'). The performance of a classifier can be represented by an ROC plot of TPR vs FPR, for a set of different threshold values of T. In particular, we have

• If $T\Longrightarrow\infty$, then $TPR=FPR=0\%$;
• If $T\Longrightarrow -\infty$, then $TPR=FPR=100\%$;
• otherwise $0\%<TPR<100\%,\;\;0\%<FPT<100\%$

As a lower/higher threshold $T$ will cause both $TPR$ and $FPR$ to become higher/lower, the ROC plot is a curve that monotonically increases. The ROC plot of a good classifier should reach to the top edge for $TPR=1$ very quickly as $FPR$ increases from 0 to 1. The area underneath the curve can be used to measure the performance of the classifier. The greater the area underneath the ROC curve, the better classification performance.

Examples

• $TPR=0.6,\;\;FNR=1-TPR=0.4,\;\;\;FPR=0.3,\;\;\;TNR=1-FPR=0.7$, the corresponding point in ROC is $(0.3,\;0.6)$ above the diagonal, better than a random guess.
• $TPR=0.6,\;\;FNR=1-TPR=0.4,\;\;\;FPR=0.6,\;\;\;TNR=1-FPR=0.4$, the corresponding point in ROC is $(0.6,\;0.6)$ on the diagonal, same as a random guess.
• $TPR=0.2,\;\;FNR=1-TPR=0.8\%,\;\;\;FPR=0.6,\;\;\;TNR=1-FPR=0.4$, the corresponding point in ROC is $(0.4,\;0.2)$ under the diagonal, worse than a random guess.