


Next: Hierarchical Classifiers
Up: classify
Previous: The AdaBoost Algorithm
A clustering algorithm groups the given samples, each represented as a
vector
![${\bf x}=[x_1,\cdots,x_N]^T $](img3.png) in the N-dimensional feature space,
into a set of clusters according to their spatial distribution in the N-D
space. Clustering is an unsupervised classification as no a priori
knowledge (such as samples of known classes) is assumed to be available.
in the N-dimensional feature space,
into a set of clusters according to their spatial distribution in the N-D
space. Clustering is an unsupervised classification as no a priori
knowledge (such as samples of known classes) is assumed to be available.
The K-Means Algorithm
This method is simple, but it has the main drawback that the number of
clusters 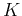 needs to be estimated based on some prior knowledge, and it
stays fixed through out the clustering process, even it may turn out later
that more or fewer clusters would fit the data better. One way to resolve
this is to carry out the algorithm multiple times with different
needs to be estimated based on some prior knowledge, and it
stays fixed through out the clustering process, even it may turn out later
that more or fewer clusters would fit the data better. One way to resolve
this is to carry out the algorithm multiple times with different 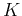 , and
then evaluate each result by some separability criteria, such as
, and
then evaluate each result by some separability criteria, such as
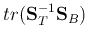 .
.
The ISODATA Algorithm
In the K-means method, the number of clusters 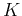 remains the same through
out the iteration, although it may turn out later that more or fewer
clusters would fit the data better. This drawback can be overcome in the
ISODATA Algorithm (Iterative Self-Organizing Data Analysis Technique
Algorithm), which allows the number of clusters to be adjusted automatically
during the iteration by merging similar clusters and splitting clusters with
large standard deviations. The algorithm is highly heuristic and based on the
following pre-specified parameters:
remains the same through
out the iteration, although it may turn out later that more or fewer
clusters would fit the data better. This drawback can be overcome in the
ISODATA Algorithm (Iterative Self-Organizing Data Analysis Technique
Algorithm), which allows the number of clusters to be adjusted automatically
during the iteration by merging similar clusters and splitting clusters with
large standard deviations. The algorithm is highly heuristic and based on the
following pre-specified parameters:
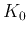 : desired number of clusters;
: desired number of clusters;
 : minimum number of samples in each cluster (for discarding
clusters);
: minimum number of samples in each cluster (for discarding
clusters);
-
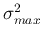 : maximum variance (for splitting clusters).
: maximum variance (for splitting clusters).
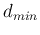 : minimum pairwise distance (for merging clusters).
: minimum pairwise distance (for merging clusters).
Here are the steps of the algorithm:
- Choose randomly
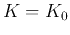 initial mean vectors
initial mean vectors
 from the data set.
from the data set.
- Assign each data point
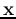 to the cluster with
closest mean:
to the cluster with
closest mean:
- Discard clusters containing too few members, i.e., if
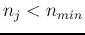 , then discard
, then discard 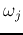 and reassign its members to
other clusters.
and reassign its members to
other clusters.
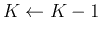 .
.
- For each cluster
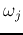
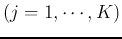 , update the mean
vector
, update the mean
vector
and the covariance matrix:
The diagonal elements are the variances
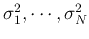 along the
along the 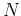 dimensions.
dimensions.
- If
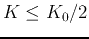 (too few clusters), go to Steps 6 for
splitting;
(too few clusters), go to Steps 6 for
splitting;
else if 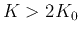 (too many clusters), go to Steps
7 for merging;
(too many clusters), go to Steps
7 for merging;
else go to Step 8.
- (split) For each cluster
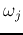
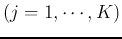 , find the
greatest covariance
, find the
greatest covariance
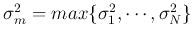
If
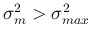 and
and
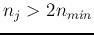 , then split
, then split
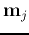 into two new cluster centers
into two new cluster centers
Alternatively, carry out PCA to find the variance corresponding to the
greatest eigenvalue 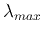 and split the cluster along the
direction along the corresponding eigenvector.
and split the cluster along the
direction along the corresponding eigenvector.
Set
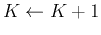 .
.
Go to Step 8.
- (merge) Compute the
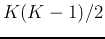 pairwise Bhattacharyya distances
between every two cluster mean vectors:
pairwise Bhattacharyya distances
between every two cluster mean vectors:
For each of the distances satisfying
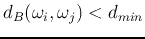 ,
merge of the corresponding clusters to form a new one:
,
merge of the corresponding clusters to form a new one:
Delete 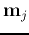 , set
, set
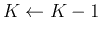 .
.
- Terminate if maximum number of iterations is reached.
Otherwise go to Step 2.
As the number of clusters 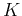 can be dynamically adjusted in the process,
the Isodata algorithm is more flexible than the K-means algorithm. But all
of the many more parameters listed previously have to be chosen empirically.
can be dynamically adjusted in the process,
the Isodata algorithm is more flexible than the K-means algorithm. But all
of the many more parameters listed previously have to be chosen empirically.



Next: Hierarchical Classifiers
Up: classify
Previous: The AdaBoost Algorithm
Ruye Wang
2016-11-30
![]() in the N-dimensional feature space,
into a set of clusters according to their spatial distribution in the N-D
space. Clustering is an unsupervised classification as no a priori
knowledge (such as samples of known classes) is assumed to be available.
in the N-dimensional feature space,
into a set of clusters according to their spatial distribution in the N-D
space. Clustering is an unsupervised classification as no a priori
knowledge (such as samples of known classes) is assumed to be available.
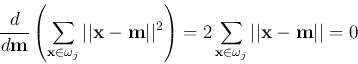
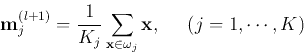
![]() , goto Step 2.
, goto Step 2.
![]() remains the same through
out the iteration, although it may turn out later that more or fewer
clusters would fit the data better. This drawback can be overcome in the
ISODATA Algorithm (Iterative Self-Organizing Data Analysis Technique
Algorithm), which allows the number of clusters to be adjusted automatically
during the iteration by merging similar clusters and splitting clusters with
large standard deviations. The algorithm is highly heuristic and based on the
following pre-specified parameters:
remains the same through
out the iteration, although it may turn out later that more or fewer
clusters would fit the data better. This drawback can be overcome in the
ISODATA Algorithm (Iterative Self-Organizing Data Analysis Technique
Algorithm), which allows the number of clusters to be adjusted automatically
during the iteration by merging similar clusters and splitting clusters with
large standard deviations. The algorithm is highly heuristic and based on the
following pre-specified parameters:
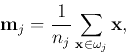
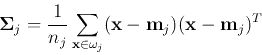
![]() (too many clusters), go to Steps
7 for merging;
(too many clusters), go to Steps
7 for merging;
![]() and
and
![]() , then split
, then split
![]() into two new cluster centers
into two new cluster centers
![]() .
.
![\begin{displaymath}
d_B(\omega_i, \omega_j)=\frac{1}{4}({\bf m}_i-{\bf m}_j)^T
...
...ight\vert)^{1/2}}\right],
\;\;\;\;\;(1\le i,j\le K,\;\;i>j)
\end{displaymath}](img328.png)
![\begin{displaymath}
{\bf m}_i=\frac{1}{n_i+n_j} [ n_i {\bf m}_i+n_j{\bf m}_j]
\end{displaymath}](img330.png)
![]() can be dynamically adjusted in the process,
the Isodata algorithm is more flexible than the K-means algorithm. But all
of the many more parameters listed previously have to be chosen empirically.
can be dynamically adjusted in the process,
the Isodata algorithm is more flexible than the K-means algorithm. But all
of the many more parameters listed previously have to be chosen empirically.