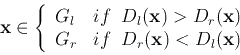Next: Feature Selection
Up: classify
Previous: Unsupervised Classification - Clustering
Both supervised classification and unsupervised clustering can be carried
out in a hierarchical fashion to classify the input patterns or group them
into clusters, very much like the hierarchy of biological classifications
with different
taxonomic ranks
(domain, kingdom, phylum, class, order, family, genus, and species).
- Unsupervised clustering
The hierarchical clustering can be obtained in either a top-down or bottom
up manner.
- Top-down method: All patterns in the data set are initially
treated as a single cluster as the root of the tree, which is then
subdivided (split) into a set of two or more smaller clusters, each
represented as a node in the tree structure. This process is carried
out recursively until eventually each cluster contains only one pattern,
represented as a leaf node of the tree.
- Bottom-up method: every pattern in the data set is initially
treated as a cluster as a leaf node of the tree, which will then be merged
to form larger clusters. Again, this process is carried out recursively
until eventually all patterns are merged into a single cluster at the root
of the tree.
In either the top-down or the bottom-up method, the specific method for
the splitting or merging at each tree node is based on certain similarity
measurement such as the distance between two clusters. The resulting tree
structure obtained by either method can then be truncated at any level
between the root and the leaf nodes to obtain a set of clusters, depending
on the desired number and sizes of these clusters.
- Supervised classification
If labeled training data are available, both the top-down and the bottom-up
clustering methods for clustering can also be used in the training stage of
the supervised classification methods with the only difference that now the
splitting or merging is applied to labeled classes instead of individual
patterns, and each leaf node represents a set of patterns all
belong to the same class, rather than a single pattern. After the tree structure
is obtained, the training is complete and any unlabeled pattern can be classified
at the tree root and then subsequently the tree nodes at lower levels until it is
classified into one of the leaf nodes of the tree, corresponding to a specific
class.
This hierarchical classification method is especially useful when the number
of classes and the dimensionality 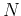 of the pattern vectors are both large,
as some feature selection algorithm can be carried out at each node of the
tree structure to use only a small number of
of the pattern vectors are both large,
as some feature selection algorithm can be carried out at each node of the
tree structure to use only a small number of 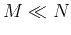 features most relevant
and suitable to represent the subset of classes associated with the node. Such
an adaptive feature selection can be much more effective compared to a single-level
classification, where all classes need to be classified at the same time,
requiring, most likely, all
features most relevant
and suitable to represent the subset of classes associated with the node. Such
an adaptive feature selection can be much more effective compared to a single-level
classification, where all classes need to be classified at the same time,
requiring, most likely, all 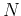 features.
features.
In the following we consider both the bottom-up and top-down methods for
hierarchical clustering/classification.
- Bottom-Up method
The bottom-up hierarchical classifier is trained based on 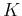 labeled
classes
labeled
classes
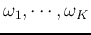 , each containing
, each containing 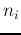 (
(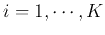 )
patterns
)
patterns
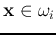 .
.
- Training:
- Estimate the mean and covariance of each cluster/class
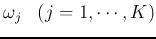 of
of 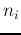 samples:
samples:
- Compute the
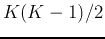 pairwise Bhattacharyya distances between
any two classes
pairwise Bhattacharyya distances between
any two classes 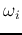 and
and 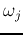 of the
of the 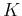 classes:
classes:
- Merge the two classes corresponding to the smallest
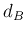 to form
a new class:
to form
a new class:
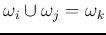 and compute its mean and covariance:
and compute its mean and covariance:
and
Delete the old classes 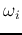 and
and 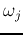 . Now there are
. Now there are 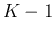 classes left.
classes left.
Compute the distance between the new class 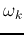 and all remaining
classes.
and all remaining
classes.
- Repeat the previous step until eventually all classes are merged
into one and a binary tree structure is thus obtained.
- Classification:
- At each node of the tree build a binary classifier to be used
to classify a pattern into one of the two children, the left and
right groups
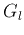 and
and 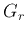 . Obtain the discriminant functions
. Obtain the discriminant functions
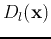 and
and 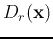 according to the specific
classification method used.
according to the specific
classification method used.
- At each node of the tree adaptively select features most suitable
for separating the two groups
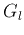 and
and 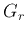 . Some feature selection
methods such as those listed below can be used.
. Some feature selection
methods such as those listed below can be used.
- Choosing
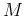 features directly from the
features directly from the 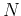 original ones using
between-class distance (Bhattacharrya distance) as the criterion,
original ones using
between-class distance (Bhattacharrya distance) as the criterion,
- Carry out KLT based on the between-class scatter matrix and
use the first
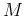 principal components for the binary classification.
principal components for the binary classification.
As here only two groups of classes need to be distinguished, the number
of features 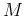 can be expected to be small.
can be expected to be small.
- After the classifier is constructed in the training process,
the classification can be carried out. Specifically, any pattern
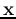 of unknown class enters the classifier at the root of the
tree and is classified to either the left or the right child of the
node according to
of unknown class enters the classifier at the root of the
tree and is classified to either the left or the right child of the
node according to
This process is repeated recursively at either of the two child nodes
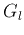 or
or 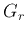 , and then in turn one of its child nodes and so on,
until eventually
, and then in turn one of its child nodes and so on,
until eventually 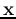 reaches one of the leaf nodes corresponding
to a single class, to which the sample
reaches one of the leaf nodes corresponding
to a single class, to which the sample 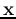 is therefore classified.
is therefore classified.
This method can also be used for unsupervised clustering, if the initialization
in the first step is for individual patterns instead of the classes in the
training data. In this case, each pattern vector 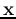 is a class of
the same mean and zero covariance matrix. Following all subsequent steps in
the training process, we obtain a clustering hierarchy when all patterns have
merged into the root node of the tree.
is a class of
the same mean and zero covariance matrix. Following all subsequent steps in
the training process, we obtain a clustering hierarchy when all patterns have
merged into the root node of the tree.
- Top-Down method
Unsupervised clustering can also be implemented hierarchically in a top-down
manner. The algorithm generates a binary tree by recursively partitioning
all patterns, treated as vectors in an N-dimensional vector space, into two
sub-groups in the following two steps:
- Compute the covariance matrix of the samples and then apply PCA method.
Specifically, find the eigenvector
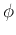 of the covariance matrix
of the covariance matrix
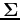 corresponding to the largest eigenvalue
corresponding to the largest eigenvalue 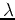 . Project
all pattern vectors
. Project
all pattern vectors 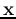 onto a 1-D space:
onto a 1-D space:
- Sort all data point along this 1-D space and partition them into two
subgroups with maximum between-group (Bhattacharyya) distance.
- Recursively carry out the two steps above to each subgroup, until each
subgroup contains only one pattern vector. Alternatively, the recursion can
be terminated when certain criterion is satisfied.
In the case of supervised classification, we find the optimal partitioning
of a set of given classes into two groups with the maximum Bhattacharyya
distance. This splitting is carried out recursively until reaching the
bottom of the tree where all leaf nodes contain one class only.
The total number of dividing a set of 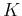 classes into two groups is
classes into two groups is
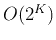 .
.
Example
The hierarchical clustering method is applied to a dataset composed of
seven normally distributed clusters each containing 25 sample vectors in an 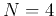 dimensional space. The PCA method is used to project the data in 4-D space into
a 2-D space spanned by the first two principal components, as shown below:
dimensional space. The PCA method is used to project the data in 4-D space into
a 2-D space spanned by the first two principal components, as shown below:

The clustering result is shown below. Each column in the display represents the
four components of a 4-D vector, color coded by a spectrum from red (low values)
through green (middle) to blue (high values).

See
more examples
in clustering analysis applied to gene data analysis in bioinformatics.
An example of this method is available here.



Next: Feature Selection
Up: classify
Previous: Unsupervised Classification - Clustering
Ruye Wang
2016-11-30
![]() of the pattern vectors are both large,
as some feature selection algorithm can be carried out at each node of the
tree structure to use only a small number of
of the pattern vectors are both large,
as some feature selection algorithm can be carried out at each node of the
tree structure to use only a small number of ![]() features most relevant
and suitable to represent the subset of classes associated with the node. Such
an adaptive feature selection can be much more effective compared to a single-level
classification, where all classes need to be classified at the same time,
requiring, most likely, all
features most relevant
and suitable to represent the subset of classes associated with the node. Such
an adaptive feature selection can be much more effective compared to a single-level
classification, where all classes need to be classified at the same time,
requiring, most likely, all ![]() features.
features.
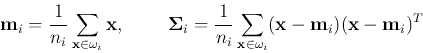
![\begin{displaymath}
d_B(\omega_i, \omega_j)=\frac{1}{4}({\bf m}_i-{\bf m}_j)^T
...
...right\vert\;\left\vert{\bf\Sigma}_j\right\vert)^{1/2}}\right]
\end{displaymath}](img70.png)
![\begin{displaymath}
{\bf m}_k=\frac{1}{n_i+n_j}[n_i {\bf m}_i+n_j {\bf m}_j]
\end{displaymath}](img339.png)
![\begin{displaymath}
{\bf\Sigma}_k=\frac{1}{n_i+n_j}
[n_i (\Sigma_i+({\bf m}_i-...
..._j (\Sigma_j+({\bf m}_j-{\bf m}_k)({\bf m}_j-{\bf m}_k)^T ) ]
\end{displaymath}](img340.png)