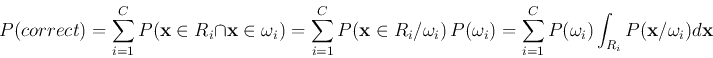Error analysis

First consider the case of $C=2$ classes. Let $P({\bf x}\in R_i \cap {\bf x}\in \omega_j)$ denote the joint probability that ${\bf x}$ belongs to $\omega_j$ but is in $R_i$ ($i,j=1,2$), then the total probability of error (misclassification) is:

$$P(error) = P(({\bf x}\in R_2) \cap ({\bf x}\in \omega_1)) +P(({\bf x}\in R_1) \cap ({\bf x}\in \omega_2))$$

$$= P({\bf x} \in R_2/\omega_1) P(\omega_1) +P({\bf x} \in R_1/\omega_2) P(\omega_2)$$

$$= \int_{R_2}p({\bf x}/\omega_1)d{\bf x} P(\omega_1) +\int_{R_1}p({\bf x}/\omega_2)d{\bf x} P(\omega_2)$$

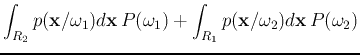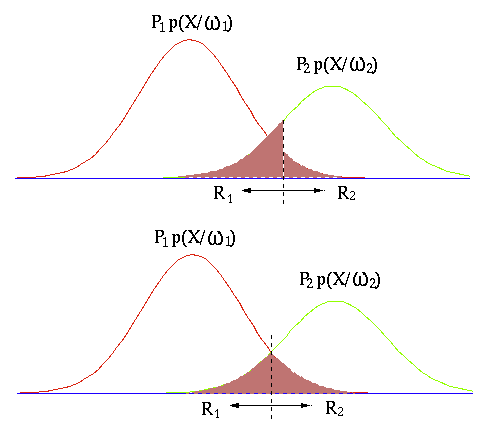
It is obvious that the Bayes classifier is indeed optimal, due to the fact that its boundaries corresponding to $D_1({\bf x})=D_2({\bf x})$ guarantee the classification error to be minimized.

Next consider multi-class case. As there are many different ways to have a wrong classification and only one way to get it right, consider

$$P(correct) =\sum_{i=1}^C P({\bf x} \in R_i \cap {\bf x} \in ... ...um_{i=1}^C P(\omega_i) \int_{R_i} P({\bf x}/\omega_i)d{\bf x}$$