Note that ![]() is the weighted sum of all
is the weighted sum of all
![]() for
for
![]() :
:
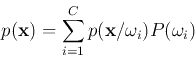
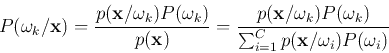
The a priori probability ![]() can be estimated from the
training samples as
can be estimated from the
training samples as
![]() , assuming the training samples
are randomly chosen from all the patterns.
, assuming the training samples
are randomly chosen from all the patterns.
We also need to estimate
![]() . If we don't have any good reason
to believe otherwise, we will assume the density to be a normal distribution:
. If we don't have any good reason
to believe otherwise, we will assume the density to be a normal distribution:
![\begin{displaymath}
p({\bf x}/\omega_i)=N({\bf x},{\bf m}_i,{\bf\Sigma}_i)=
\fra...
...f x}-{\bf m}_i)^T {\bf\Sigma}_i^{-1}({\bf x}-{\bf m}_i)\right]
\end{displaymath}](img150.png)
where the mean vector
A given pattern ![]() of unknown class is classified to
of unknown class is classified to ![]() if
it is most likely to belong to
if
it is most likely to belong to ![]() (optimal classifier), i.e.:
(optimal classifier), i.e.:
As shown above, the likelihood
![]() can be written as
can be written as
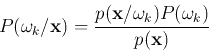
and the denominator
can be used in the classification:
Give all