


Next: Vector norms
Up: algebra
Previous: Singular value decomposition
Let 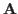 be an
be an 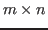 matrix. If
matrix. If 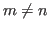 , then
, then 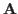 does not
have an inverse. However, we can find its pseudo-inverse
does not
have an inverse. However, we can find its pseudo-inverse 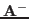 ,
an
,
an 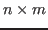 matrix, as shown below.
matrix, as shown below.
- If
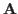 has more rows than columns; i.e.,
has more rows than columns; i.e., 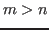 , then
, then
We can verify that
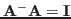 :
:
But
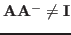 .
.
- If
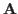 has more columns than rows; i.e.,
has more columns than rows; i.e., 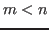 , then
, then
We can verify that
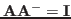 :
:
But
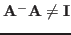 .
.
Note that the two pseudo-inverses defined above for 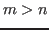 and
and 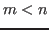 are essentially
the same. To see this, we first assume
are essentially
the same. To see this, we first assume 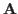 has more rows than columns (
has more rows than columns (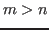 ),
then another matrix defined as
),
then another matrix defined as
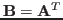 has more columns than rows. Taking
the transpose on both sides of the first pseudo inverse above, we get
has more columns than rows. Taking
the transpose on both sides of the first pseudo inverse above, we get
i.e.,
which is the same as the second definition of the pseudo inverse.
We can also show that
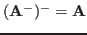 . If
. If 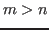 , then we have
, then we have
Similarly. we can show the same is true if 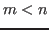 . In particular, when
. In particular, when 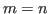 ,
,
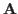 is invertible and both versions of the pseudo-inverse defined above
become the regular inverse
is invertible and both versions of the pseudo-inverse defined above
become the regular inverse
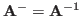 .
.



Next: Vector norms
Up: algebra
Previous: Singular value decomposition
Ruye Wang
2015-04-27
![]() be an
be an ![]() matrix. If
matrix. If ![]() , then
, then ![]() does not
have an inverse. However, we can find its pseudo-inverse
does not
have an inverse. However, we can find its pseudo-inverse ![]() ,
an
,
an ![]() matrix, as shown below.
matrix, as shown below.
![]() and
and ![]() are essentially
the same. To see this, we first assume
are essentially
the same. To see this, we first assume ![]() has more rows than columns (
has more rows than columns (![]() ),
then another matrix defined as
),
then another matrix defined as
![]() has more columns than rows. Taking
the transpose on both sides of the first pseudo inverse above, we get
has more columns than rows. Taking
the transpose on both sides of the first pseudo inverse above, we get
![]() . If
. If ![]() , then we have
, then we have