Summary of BP training

The following steps are for any randomly chosen training pattern pair $\{{\bf x}_p, {\bf y}_p\}$.

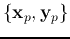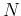1. Apply ${\bf x}_p=[x_{p1},\cdots, x_{pN}]^T$ to the $N$ input nodes;

2. Compute output from all 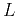$L$ nodes in the hidden layer:
   $$z_{pj}=g(net^h_{pj})=g\left( \sum_{k=1}^N w_{jk}^{h} x_{pk}+T^h_j \right), \;\;\;\;\;\;\;\;(j=1,\cdots,L)$$
3. Compute output from all 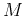$M$ nodes in the output layer:
   $$y'_{pi}=g(net^o_{pi})=g\left(\sum_{j=1}^L w_{ij}^{o} z_{pj} + T^o_i\right), \;\;\;\;\;\;\;\;\;(i=1,\cdots,M)$$
4. Find the error term for each output node (not quite the same as defined previously):
   $$\delta_{pi}^{o}=g'(net^o_{pi}) (y_{pi}-y'_{pi}) \;\;\;\;\;\;\;\;(i=1,\cdots,M)$$
5. Find error terms for all hidden nodes (not quite the same as defined previously)
   $$\delta_{pj}^{h}=g'(net^h_{pj}) \sum_{i=1}^M \delta_{pi}^{o} w_{ij}^o \;\;\;\;\;\;\;(j=1,\cdots,L)$$
6. Update weights to output nodes
   $$w_{ij}^o \leftarrow w_{ij}^o+\eta \delta_{pi}^o z_{pj}\;\;\;\;\;\;\;(i=1,\cdots,m,\;\;j=1,\cdots,l)$$
7. Update weights to hidden nodes
   $$w_{jk}^h \leftarrow w_{jk}^h+\eta \delta_{pj}^h x_{pk}\;\;\;\;\;\;\;(j=1,\cdots,l,\;\;k=1,\cdots,n)$$
8. Compute
   $$e_p=\frac{1}{2}\sum_{i=1}^M (y_{pi}-y'_{pi})^2$$

This process is then repeated with another pair of 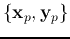$\{{\bf x}_p, {\bf y}_p\}$ in the training set. When the error is acceptably small for all of the training pattern pairs, training can be terminated.

The training process of BP network can be considered as a data modeling problem:

$${\bf y}_p={\bf f}({\bf x}_p,{\bf w})$$

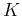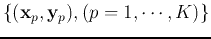The goal is to find the optimal parameters, the weights of both the hidden and output layers, based on the observed dataset, the training data of $K$ pairs $\{ ( {\bf x}_p,{\bf y}_p), (p=1,\cdots,K)\}$. The Levenberg-Marquardt algorithm discussed previously can be used to obtain the parameters, such as Matlab function trainlm