Next: Summary of BP training Up: Introduction to Neural Networks Previous: Perceptron Learning
The back propagation network (BPN) is a typical supervised network
composed of three hierarchical layers: the input, hidden, and output layers
with ![]() ,
, ![]() , and
, and ![]() nodes, respectively. Each node in the hidden and
output layers is fully connected to all nodes in the previous layer. As
the BPN has two levels of learning takeing place at both the hidden and
output layers, it is a much more powerful algorithm in comparison to the
perceptron network which has only a single learning level, in the sense
that it can handle more complicated nonlinear classification problems.
nodes, respectively. Each node in the hidden and
output layers is fully connected to all nodes in the previous layer. As
the BPN has two levels of learning takeing place at both the hidden and
output layers, it is a much more powerful algorithm in comparison to the
perceptron network which has only a single learning level, in the sense
that it can handle more complicated nonlinear classification problems.
For example, in supervised classification, the number of output nodes
![]() can be set to be the same as the number of classes
can be set to be the same as the number of classes ![]() , i.e.,
, i.e., ![]() ,
and the desired output for an input
,
and the desired output for an input ![]() belonging to class
belonging to class ![]() is
is
![]() , for all output nodes to output 0
except the c-th one which should output 1 (one-hot method).
, for all output nodes to output 0
except the c-th one which should output 1 (one-hot method).
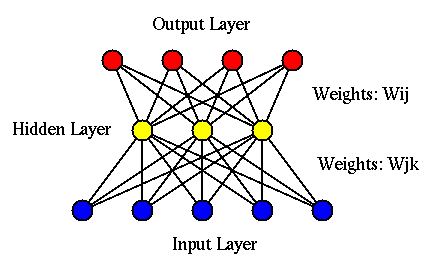
Based on the training set of ![]() pattern pairs
pattern pairs
![]() , where
, where ![]() is the input patterns
and
is the input patterns
and ![]() is the desired response of the network corresponding the
output, the two-level BPN network is trained in two phases:
is the desired response of the network corresponding the
output, the two-level BPN network is trained in two phases:
When an input of ![]() components
components
![]() randomly selected from the training set is presented to the
randomly selected from the training set is presented to the ![]() input layer nodes, the net input to the jth hidden node is:
input layer nodes, the net input to the jth hidden node is:

The output of the jth hidden node is a sigmoid function of its net input:

The net input to the ith node of the output layer is:

The output of the ith output node is a sigmoid function of its net input:

The desired output ![]() corresponding to the input
corresponding to the input ![]() is compared with the actual output of the network, now denoted by
is compared with the actual output of the network, now denoted by
![]() as a function of all the weights and thresholds
involved in the two levels of computation in the forward pass, to
define the error function:
as a function of all the weights and thresholds
involved in the two levels of computation in the forward pass, to
define the error function:
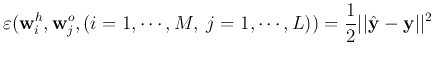 |
|||
![$\displaystyle \frac{1}{2}\sum_{i=1}^M (\hat{y}_i-y_i)^2
=\frac{1}{2}\sum_{i=1}^...
...rac{1}{2}\sum_{i=1}^M \left[g\left(\sum_{j=0}^L w_{ij}^oz_j\right)-y_i\right]^2$](img49.svg) |
|||
![$\displaystyle \frac{1}{2}\sum_{i=1}^M\left[g\left(\sum_{j=0}^L w_{ij}^o\,g(q_j)...
...m_{j=0}^L w_{ij}^o\,
g\left(\sum_{k=0}^N w_{jk}^hx_k\right)\right)-y_i\right]^2$](img50.svg) |
The goal of the training is to minimize this error function
![]() for all samples in the training set by the
gradient descent method. Specifically, the weights and the
thresholds are to be optimized so that the sigmoid functions
for all samples in the training set by the
gradient descent method. Specifically, the weights and the
thresholds are to be optimized so that the sigmoid functions
![]() and
and
![]() are properly shaped in
such a way that they best fit the output
are properly shaped in
such a way that they best fit the output ![]() of the
BPN with the corresponding input
of the
BPN with the corresponding input ![]() for all
for all ![]() .
.
The backward propagation is also carried out in two levels:
Find the gradient of the error function ![]() in the output
weight space
in the output
weight space ![]() (
(
![]() ) by the
chain rule:
) by the
chain rule:


Find the gradient of ![]() in the hidden weight space
in the hidden weight space
![]() (
(
![]() ):
):
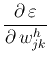 |
 |
||
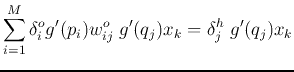 |

