Self-organizing property of the SOM

More detailed information related to the following discussion can be found in this paper, presented at The 11th International Conference on Natural Computation(ICNC'15).

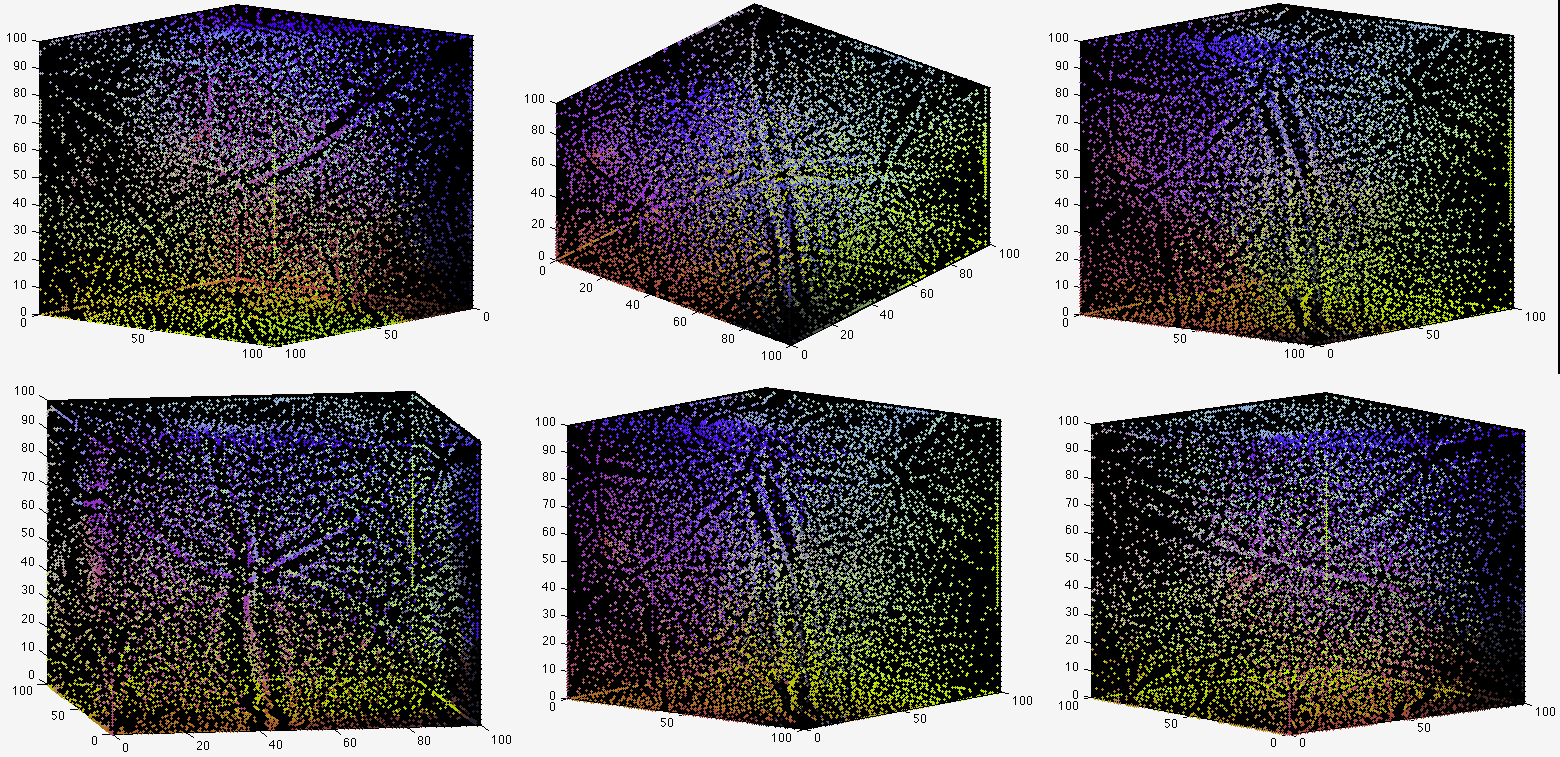
In the SOMs shown below, the number of training samples increases in horizontal direction ($4^3=64$, $6^3=216$, $8^3=512$, $10^3=1,000$, $20^3=8,000$, $40^3=64,000$), while the size of the SOM increases in vertical direction ($20\time 20$, $40\time 40$, $60\time 60$, $80\time 80$, $100\time 100$, $200\time 200$).

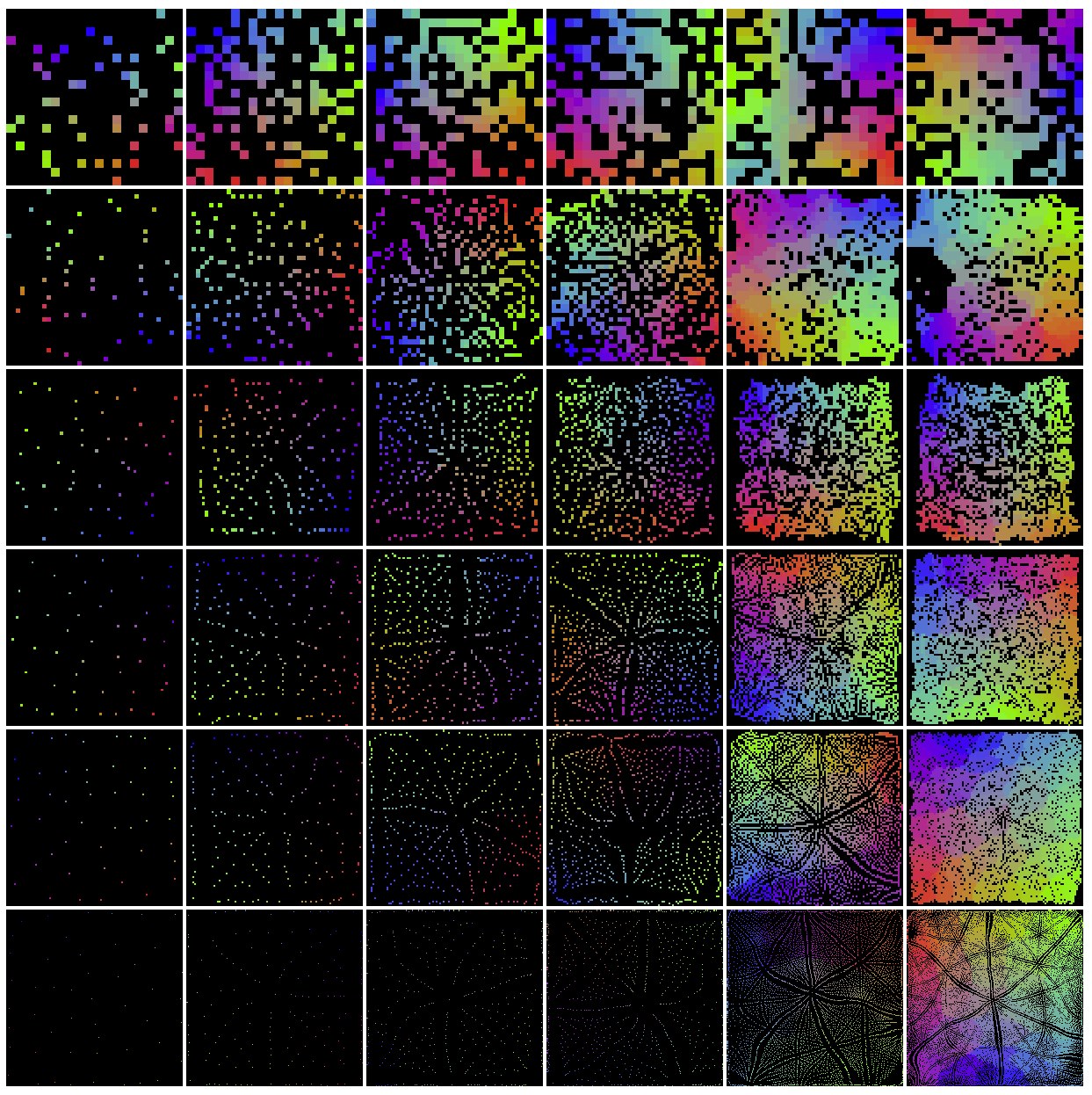
The SOMs in the figure below all have the same size of $300\times 300$, while the number of color vectors increase in horizontal direction ($6^3=216$, $8^3=512$, $10^3=1,000$, $20^3=8,000$, $40^3=64,000$). The Gaussian width $\sigma$ is 1/3 of the size of the SOM.

The SOMs in the figure below are similar to the previous ones except the SOMs have the same size of $400\times 400$.

The four images below are obtained after 18, 19, 20, and 21 training iterations, respectively, show how the patterns start to emerge from random distributions of the nodes responding to the training samples. More examples can be found here.

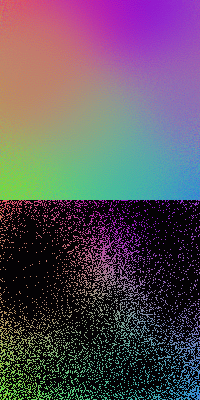
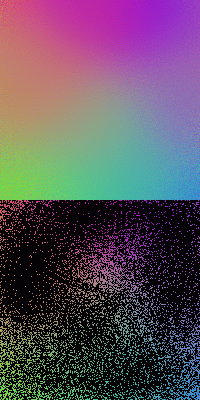
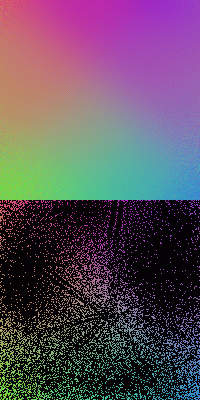
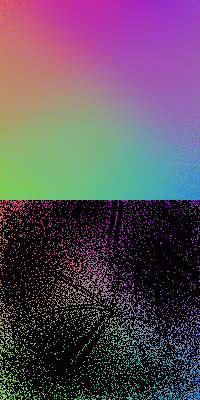
The figures below show the SOMs of size $600\times 600$ trained by $50^3=125,000$ samples. Here a smaller Gaussian width $\sigma$ (1/12 of the SOM size for the first two, 1/10 for the third) is used, consequently the resulting SOMs are less continuous and homogeneous in comparison to the SOMs trained with greater $\sigma$. The first and last SOMs are trained by 3000 iterations, while the middle one by 4000.

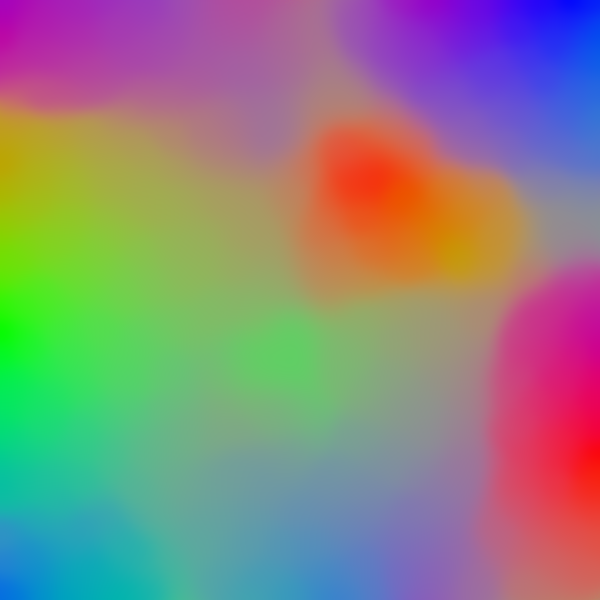
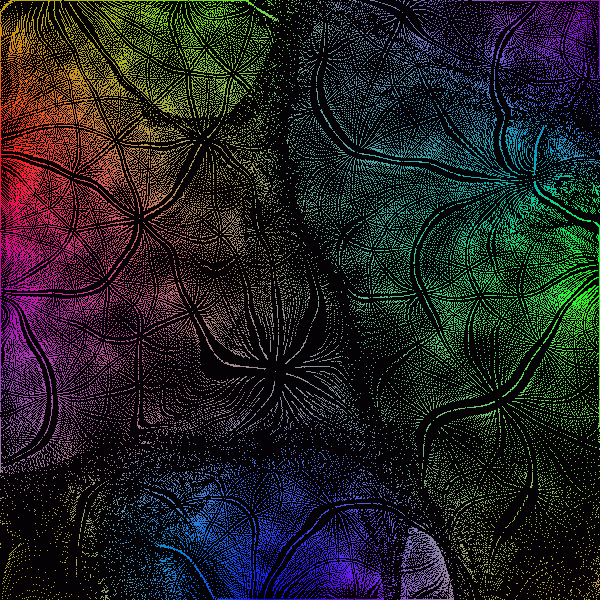
The image below is the SOM of size $1,000\times 1,000$, trained by $100^3=1,000,000$ color vectors, with $\sigma$ equal to 1/3 of the size.

The image below is the same as before, with the only difference that here $\sigma$ is reduced from 1/3 to 1/12 of the size of the SOM.

Below is a SOM of $2000\times 2000$ ($\sigma=1/3$ and $\sigma=1/10$ of image size).

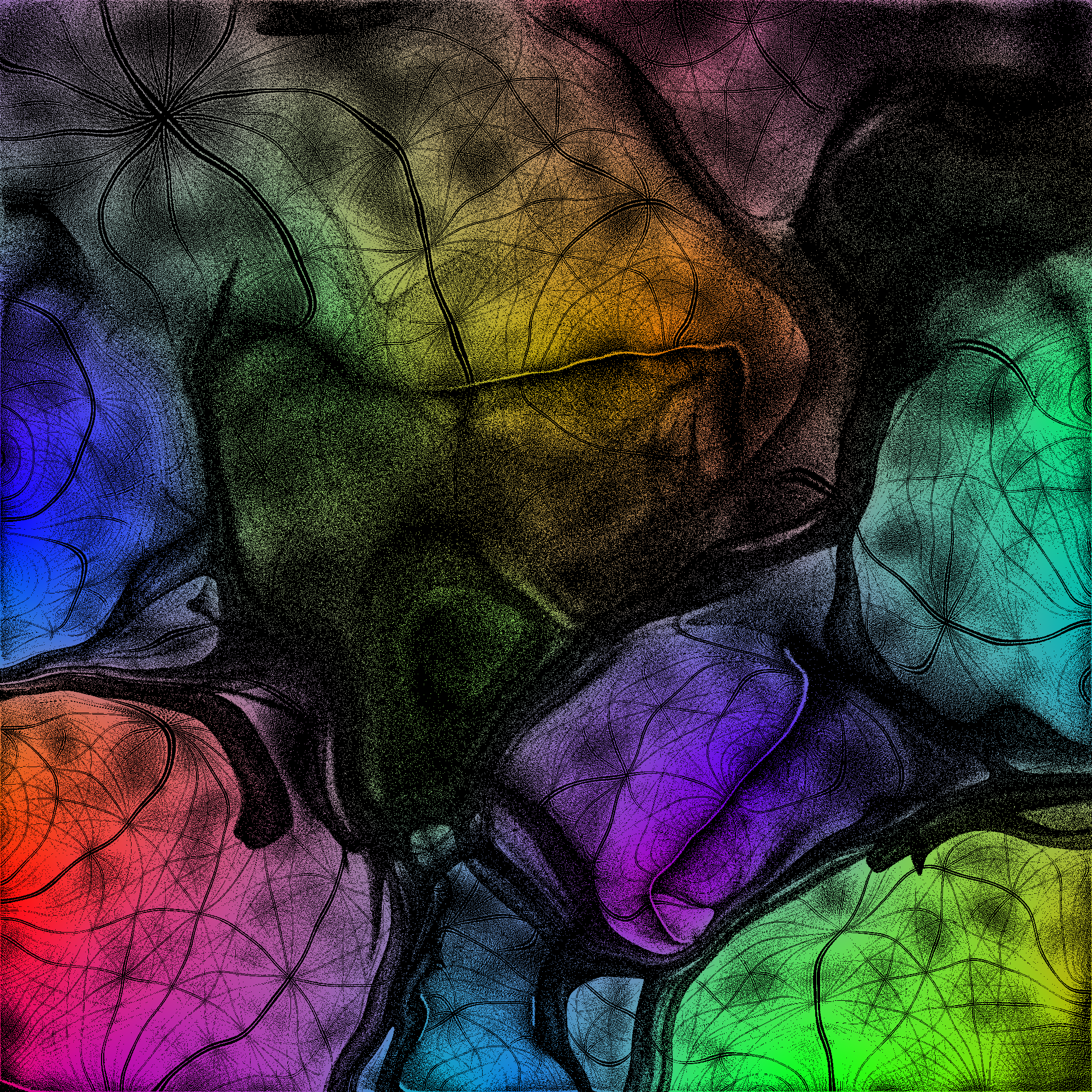
The image below is yet another SOM of size $8192\times 8192$ (generated by Kyle Lund, a student at HMC):

The figure below is the 2-D SOM trained by a set of 4-D vector samples. Although there seem to be some patterns in the image, they are not as obvious as those in the SOMs trained by 3-D vector samples.

This figure below shows the 3-D SOM trained by a set of 4-D vector samples. There are some obvious patterns in the SOM, very similar to those in a 2-D SOM.