We first consider a first-order ODE system composed of a set of
 simultaneous first-order explicit ODEs:
simultaneous first-order explicit ODEs:
 |
(109) |
The goal is to find the  functions
functions
 that
satisfy these
that
satisfy these  equations based on the
equations based on the  initial conditions
initial conditions

 . This system can be represented
in vector form:
. This system can be represented
in vector form:
 |
(110) |
where
![$\displaystyle {\bf y}(t)=\left[\begin{array}{c}y_1(t)\\ \vdots\\ y_N(t)\end{arr...
...{array}{c}f_1(t,\,{\bf y}(t))\\
\vdots\\ f_N(t,\,{\bf y}(t))\end{array}\right]$](img286.svg) |
(111) |
Consider as an example a special ODE system containing  first-order LCCODEs:
first-order LCCODEs:
![$\displaystyle \frac{d}{dt}\left[\begin{array}{c}y_1(t)\\ \vdots\\ y_N(t)\end{ar...
...array}\right]
+\left[\begin{array}{c}x_1(t)\\ \vdots\\ x_N(t)\end{array}\right]$](img287.svg) |
(112) |
which can be expressed in matrix form as
 or or |
(113) |
First, to find the homogeneous solution when
 ,
we assume
,
we assume
 and substitute this into
the ODE system to get:
and substitute this into
the ODE system to get:
 |
(114) |
Dividing both sides by
 , we get the eigenequation of
, we get the eigenequation of
 :
:
 |
(115) |
where  is an eigenvalue of
is an eigenvalue of  and
and  is the
corresponding eigenvector. In general, there are
is the
corresponding eigenvector. In general, there are  eigenvalues
eigenvalues
 and
and  corresponding eigenvectors
corresponding eigenvectors
 for an
for an  by
by  matrix
matrix  ,
and the homogeneous solution is a linear combination of all
,
and the homogeneous solution is a linear combination of all  such
solutions:
such
solutions:
![$\displaystyle {\bf y}_h(t)=\sum_{i=1}^N c_i e^{\lambda_it}{\bf v}_i
=[{\bf v}_1...
...array}{c} c_1\\ \vdots\\ c_N\end{array}\right]
={\bf V}e^{{\bf\Lambda}t}{\bf c}$](img300.svg) |
(116) |
where
 is a matrix exponential function, which
is generally defined based on the Taylor expansion of an
exponential function:
is a matrix exponential function, which
is generally defined based on the Taylor expansion of an
exponential function:
 |
(117) |
Specially when
 is a diagonal matrix,
we have
is a diagonal matrix,
we have
![$\displaystyle e^{\bf\Lambda t}
={\bf I}+{\bf\Lambda t}+\frac{1}{2!}{\bf\Lambda}...
...&&e^{\lambda_Nt}
\end{array}\right]
=diag[e^{\lambda_1t},\cdots,e^{\lambda_Nt}]$](img304.svg) |
(118) |
The  coefficients in
coefficients in
![${\bf c}=[c_1,\cdots,c_N]^T$](img305.svg) can be found
based on the
can be found
based on the  given initial conditions
given initial conditions
 :
:
 |
(119) |
Solving for  we get
we get
 .
Substituting this back to the general solution we get:
.
Substituting this back to the general solution we get:
 |
(120) |
But as the eigenvalue and eigenvector matrices
 and
and  of
of  satisfy
satisfy
 or
or
 , we have
, we have
Therefore the homogeneous solution can be written as
 |
(122) |
Next, in the non-homogeneous case when
 , the
complete solution of the first-order LCCODE system can again be
found analytically. We first multiply
, the
complete solution of the first-order LCCODE system can again be
found analytically. We first multiply
 on both sides
of the ODE
on both sides
of the ODE
 and get
and get
![$\displaystyle e^{-{\bf A}t} {\bf y}'(t)-e^{-{\bf A}t}{\bf Ay}(t)
=\frac{d}{dt}\left[ e^{-{\bf A}t} {\bf y}(t) \right] =e^{-{\bf A}t}{\bf x}(t)$](img321.svg) |
(123) |
Integrating both sides we get
 |
(124) |
Multiplying
 on both side and rearranging we get
on both side and rearranging we get
 |
(125) |
where
 is the homogeneous solution
same as that found previously, and
is the homogeneous solution
same as that found previously, and
 is the particular
solutions, the system response to the input
is the particular
solutions, the system response to the input
 . Specially
when
. Specially
when
 is an impulse function, the system
response is the impulse response of the system:
is an impulse function, the system
response is the impulse response of the system:
 |
(126) |
i.e., the particular solution is the convolution of the impulse response
and the input:
 |
(127) |
The stability of the solution found above depends on the eigenvalues
 . If they all have negative real part,
then the solution
. If they all have negative real part,
then the solution
 is stable at it will always converge
to
is stable at it will always converge
to  . However, if one or more eigenvalues have positive real
parts while others have negative parts, a saddle point, then the
solution is unstable as it will approach
. However, if one or more eigenvalues have positive real
parts while others have negative parts, a saddle point, then the
solution is unstable as it will approach  as
as
 .
.
We next consider an Nth-order scalar ODE in the following
explicit form
 |
(128) |
The goal is to find  satisfying this equation and some
given initial condition
satisfying this equation and some
given initial condition  . To solve this DE, we can
convert it into a first-order ODE system containing
. To solve this DE, we can
convert it into a first-order ODE system containing  first-order ODEs. Specifically, we define
first-order ODEs. Specifically, we define
 (
(
 ) and represent these
) and represent these  functions in vector
form:
functions in vector
form:
![$\displaystyle {\bf y}(t)=\left[\begin{array}{c}y_1(t)\\ y_2(t)\\ y_3(t)\\ \vdot...
...t)\\ y'_1(t)\\ y'_2(t)\\ \vdots\\ y'_{N-2}(t)\\ y'_{N-1}(t)
\end{array} \right]$](img338.svg) |
(129) |
so that the Nth-order ODE can be convered into  first-order
ODEs:
first-order
ODEs:
![$\displaystyle \frac{d}{dt}{\bf y}(t)={\bf y}'(t)
=\left[\begin{array}{c}y'_1(t)...
... \vdots\\ y_N(t)\\ f(t,\,{\bf y}(t))\end{array}\right]
={\bf f}(t,\,{\bf y}(t))$](img339.svg) |
(130) |
The last equation is the original Nth-order ODE:
Reconsider as an example the second order LCCODE in canonical
form:
 |
(132) |
Here we first convert it into a first order equation system by
introducing
 :
:
 |
(133) |
or in matrix form
![$\displaystyle {\bf y}'(t)=\left[\begin{array}{c}y_1'(t)\\ y_2'(t)\end{array}\ri...
...ray}\right]
+\left[\begin{array}{c}0\\ x(t)\end{array}\right]
={\bf Ay}+{\bf x}$](img346.svg) |
(134) |
To solve this system, we first solve the eigenvalue problem of the
coefficient matrix  . Solving its characteristic equation:
. Solving its characteristic equation:
![$\displaystyle \det(\lambda{\bf I}-{\bf A})
=\det\left[\begin{array}{cc}\lambda ...
...2\zeta\omega_n
\end{array}\right]
=\lambda^2+2\zeta\omega_n\lambda+\omega_n^2=0$](img347.svg) |
(135) |
we get the eigenvalues of  the two eigenvalues and the
eigenvalue matrix:
the two eigenvalues and the
eigenvalue matrix:
![$\displaystyle \lambda_{1,2}=\left(-\zeta\pm\sqrt{\zeta^2-1}\right)\omega_n
=\le...
...\Lambda}=\left[\begin{array}{cc}\lambda_1 & 0\\ 0 & \lambda_2\end{array}\right]$](img348.svg) |
(136) |
Note that
 |
(137) |
The corresponding eigenvectors can be found by solving the following
homogeneous equation:
![$\displaystyle (\lambda_i{\bf I}-{\bf A}) {\bf v}_i
=\left[\begin{array}{cc}\lam...
...rray}\right]
=\left[\begin{array}{c}0\\ 0\end{array}\right],\;\;\;\;\;\;(i=1,2)$](img350.svg) |
(138) |
to get
![${\bf v}_1=[1,\;\lambda_1]^T$](img351.svg) and
and
![${\bf v}_2=[1,\;\lambda_2]^T$](img352.svg) ,
and
,
and
![$\displaystyle {\bf V}=\left[\begin{array}{cc}1 & 1\\ \lambda_1 & \lambda_2\end{...
...bda_1}
\left[\begin{array}{cc}\lambda_2 & -1\\ -\lambda_1 & 1\end{array}\right]$](img353.svg) |
(139) |
and we can verify thatat
 . The general form
of the homogeneous solution is
. The general form
of the homogeneous solution is
![$\displaystyle {\bf y}=\left[\begin{array}{c}y_1\\ y_2\end{array}\right]
=c_1 {\...
...bda_1t}
+c_2\left[\begin{array}{c}1\\ \lambda_2\end{array}\right]e^{\lambda_2t}$](img354.svg) |
(140) |
i.e.,
 |
(141) |
- Homogeneous case:
We have  and assume
and assume
 and
and
 .
Evaluating the general solution above at
.
Evaluating the general solution above at  , we get:
, we get:
 |
(142) |
Solving this we get
 |
(143) |
Substituting into
 above, we get:
above, we get:
 |
(144) |
Alternatively, we can also get
we get the same result as shown above:
 |
(145) |
- Nonhomogeneous case:
We assume  and zero initial conditions
and zero initial conditions
 ,
i.e.,
,
i.e.,
![${\bf x}=[0,\;1]^T$](img367.svg) and
and
 , and get:
, and get:
![$\displaystyle {\bf y}(t)=e^{{\bf A}t}{\bf y}(0)+e^{{\bf A}t}\int_0^t e^{-{\bf A}\tau}{\bf x}(\tau)d\tau
=e^{{\bf A}t}\int_0^t e^{-{\bf A}\tau} d\tau \;[0,\;1]^T$](img369.svg) |
(146) |
and
![$\displaystyle y_h(t)=y_1(t)=[1,\;0]\;{\bf y}(t)=[1,\;0]\; e^{{\bf A}t}\int_0^t e^{-{\bf A}\tau} d\tau\; [0,\;1]^T$](img370.svg) |
(147) |
where
 |
(148) |
Substituting
 |
(149) |
into the function, we get
Example 2: A tuned mass-damper-spring system shown below is
described by the following ODEs:
 |
(150) |
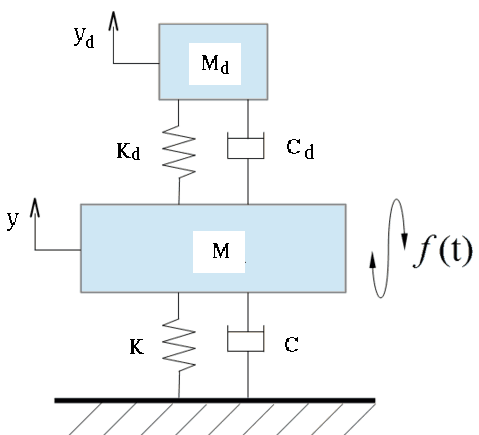
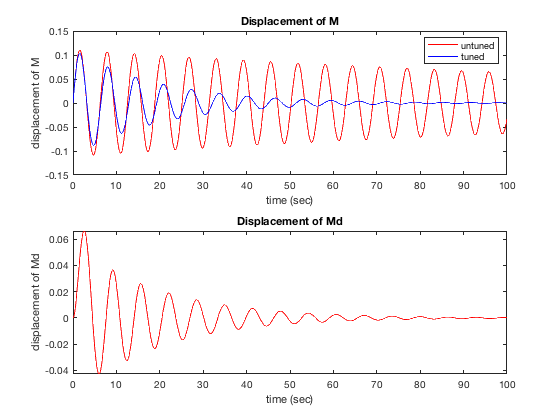
This 2nd-order ODE system can be converted into a 1st-order ODE
system by introducing  and
and  :
:
![$\displaystyle \left\{\begin{array}{l}
y'=v\\
v'=[-Ky-Cy'-K_d(y-y_d)-C_d(y'-y_d')+f]/M\\
y_d'=v_d\\
v_d'=[K_d(y-y_d)+C_d(y'-y_d')/M_d\end{array}\right.$](img380.svg) |
(151) |
or in matrix form
![$\displaystyle {\bf y}'=
\left[\begin{array}{c}y'\\ v'\\ y_d'\\ v_d'\end{array}\...
...eft[\begin{array}{c}0\\ \frac{f}{M}\\ 0\\ 0\end{array}\right]
={\bf Ay}+{\bf x}$](img381.svg) |
(152) |
Specifically, if we assume
 (modeling an earthquake)
i.e.,
(modeling an earthquake)
i.e.,
![${\bf x}=[0,\;\delta(t)/M,\;0,\;0]^T$](img383.svg) , and all zero initial
condition
, and all zero initial
condition
 , then we get:
, then we get:
 |
(153) |
and  as the first component of
as the first component of  is
is
 |
(154) |
where
 and
and  are respectively the first row
of
are respectively the first row
of  and the second column of
and the second column of
 .
.


 functions
functions
 that
satisfy these
that
satisfy these  equations based on the
equations based on the  initial conditions
initial conditions

 . This system can be represented
in vector form:
. This system can be represented
in vector form:

![$\displaystyle {\bf y}(t)=\left[\begin{array}{c}y_1(t)\\ \vdots\\ y_N(t)\end{arr...
...{array}{c}f_1(t,\,{\bf y}(t))\\
\vdots\\ f_N(t,\,{\bf y}(t))\end{array}\right]$](img286.svg)

![$\displaystyle \frac{d}{dt}\left[\begin{array}{c}y_1(t)\\ \vdots\\ y_N(t)\end{ar...
...array}\right]
+\left[\begin{array}{c}x_1(t)\\ \vdots\\ x_N(t)\end{array}\right]$](img287.svg)
 or
or
 ,
we assume
,
we assume
 and substitute this into
the ODE system to get:
and substitute this into
the ODE system to get:

 , we get the eigenequation of
, we get the eigenequation of
 :
:

 is an eigenvalue of
is an eigenvalue of  and
and  is the
corresponding eigenvector. In general, there are
is the
corresponding eigenvector. In general, there are  eigenvalues
eigenvalues
 and
and  corresponding eigenvectors
corresponding eigenvectors
 for an
for an  by
by  matrix
matrix  ,
and the homogeneous solution is a linear combination of all
,
and the homogeneous solution is a linear combination of all  such
solutions:
such
solutions:
![$\displaystyle {\bf y}_h(t)=\sum_{i=1}^N c_i e^{\lambda_it}{\bf v}_i
=[{\bf v}_1...
...array}{c} c_1\\ \vdots\\ c_N\end{array}\right]
={\bf V}e^{{\bf\Lambda}t}{\bf c}$](img300.svg)
 is a matrix exponential function, which
is generally defined based on the Taylor expansion of an
exponential function:
is a matrix exponential function, which
is generally defined based on the Taylor expansion of an
exponential function:

 is a diagonal matrix,
we have
is a diagonal matrix,
we have
![$\displaystyle e^{\bf\Lambda t}
={\bf I}+{\bf\Lambda t}+\frac{1}{2!}{\bf\Lambda}...
...&&e^{\lambda_Nt}
\end{array}\right]
=diag[e^{\lambda_1t},\cdots,e^{\lambda_Nt}]$](img304.svg)
 coefficients in
coefficients in
![${\bf c}=[c_1,\cdots,c_N]^T$](img305.svg) can be found
based on the
can be found
based on the  given initial conditions
given initial conditions
 :
:

 we get
we get
 .
Substituting this back to the general solution we get:
.
Substituting this back to the general solution we get:

 and
and  of
of  satisfy
satisfy
 or
or
 , we have
, we have









![$\displaystyle e^{-{\bf A}t} {\bf y}'(t)-e^{-{\bf A}t}{\bf Ay}(t)
=\frac{d}{dt}\left[ e^{-{\bf A}t} {\bf y}(t) \right] =e^{-{\bf A}t}{\bf x}(t)$](img321.svg)

 on both side and rearranging we get
on both side and rearranging we get

 is the homogeneous solution
same as that found previously, and
is the homogeneous solution
same as that found previously, and
 is the particular
solutions, the system response to the input
is the particular
solutions, the system response to the input
 . Specially
when
. Specially
when
 is an impulse function, the system
response is the impulse response of the system:
is an impulse function, the system
response is the impulse response of the system:








 satisfying this equation and some
given initial condition
satisfying this equation and some
given initial condition  . To solve this DE, we can
convert it into a first-order ODE system containing
. To solve this DE, we can
convert it into a first-order ODE system containing  first-order ODEs. Specifically, we define
first-order ODEs. Specifically, we define
 (
(
 ) and represent these
) and represent these  functions in vector
form:
functions in vector
form:
![$\displaystyle {\bf y}(t)=\left[\begin{array}{c}y_1(t)\\ y_2(t)\\ y_3(t)\\ \vdot...
...t)\\ y'_1(t)\\ y'_2(t)\\ \vdots\\ y'_{N-2}(t)\\ y'_{N-1}(t)
\end{array} \right]$](img338.svg)
 first-order
ODEs:
first-order
ODEs:
![$\displaystyle \frac{d}{dt}{\bf y}(t)={\bf y}'(t)
=\left[\begin{array}{c}y'_1(t)...
... \vdots\\ y_N(t)\\ f(t,\,{\bf y}(t))\end{array}\right]
={\bf f}(t,\,{\bf y}(t))$](img339.svg)






 :
or in matrix form
:
or in matrix form
![$\displaystyle {\bf y}'(t)=\left[\begin{array}{c}y_1'(t)\\ y_2'(t)\end{array}\ri...
...ray}\right]
+\left[\begin{array}{c}0\\ x(t)\end{array}\right]
={\bf Ay}+{\bf x}$](img346.svg)
 . Solving its characteristic equation:
. Solving its characteristic equation:
![$\displaystyle \det(\lambda{\bf I}-{\bf A})
=\det\left[\begin{array}{cc}\lambda ...
...2\zeta\omega_n
\end{array}\right]
=\lambda^2+2\zeta\omega_n\lambda+\omega_n^2=0$](img347.svg)
 the two eigenvalues and the
eigenvalue matrix:
the two eigenvalues and the
eigenvalue matrix:
![$\displaystyle \lambda_{1,2}=\left(-\zeta\pm\sqrt{\zeta^2-1}\right)\omega_n
=\le...
...\Lambda}=\left[\begin{array}{cc}\lambda_1 & 0\\ 0 & \lambda_2\end{array}\right]$](img348.svg)

![$\displaystyle (\lambda_i{\bf I}-{\bf A}) {\bf v}_i
=\left[\begin{array}{cc}\lam...
...rray}\right]
=\left[\begin{array}{c}0\\ 0\end{array}\right],\;\;\;\;\;\;(i=1,2)$](img350.svg)
![${\bf v}_1=[1,\;\lambda_1]^T$](img351.svg) and
and
![${\bf v}_2=[1,\;\lambda_2]^T$](img352.svg) ,
and
,
and
![$\displaystyle {\bf V}=\left[\begin{array}{cc}1 & 1\\ \lambda_1 & \lambda_2\end{...
...bda_1}
\left[\begin{array}{cc}\lambda_2 & -1\\ -\lambda_1 & 1\end{array}\right]$](img353.svg)
 . The general form
of the homogeneous solution is
. The general form
of the homogeneous solution is
![$\displaystyle {\bf y}=\left[\begin{array}{c}y_1\\ y_2\end{array}\right]
=c_1 {\...
...bda_1t}
+c_2\left[\begin{array}{c}1\\ \lambda_2\end{array}\right]e^{\lambda_2t}$](img354.svg)







 above, we get:
above, we get:



![$\displaystyle e^{{\bf A}t}{\bf y}(0)={\bf V}e^{{\bf\Lambda}t}{\bf V}^{-1}{\bf y...
...\lambda_1&1\end{array}\right]
\left[\begin{array}{c} y_0 \\ 0\end{array}\right]$](img363.svg)

![$\displaystyle \frac{1}{\lambda_2-\lambda_1}
\left[\begin{array}{cc} \lambda_2e^...
...\lambda_1t}\end{array}\right]
\left[\begin{array}{c} y_0 \\ 0\end{array}\right]$](img364.svg)

![$\displaystyle \frac{y_0}{\lambda_2-\lambda_1}
\left[\begin{array}{c} \lambda_2e...
...bda_2t}\\
\lambda_1\lambda_2(e^{\lambda_1t}-e^{\lambda_2t})
\end{array}\right]$](img365.svg)



![${\bf x}=[0,\;1]^T$](img367.svg)

![$\displaystyle {\bf y}(t)=e^{{\bf A}t}{\bf y}(0)+e^{{\bf A}t}\int_0^t e^{-{\bf A}\tau}{\bf x}(\tau)d\tau
=e^{{\bf A}t}\int_0^t e^{-{\bf A}\tau} d\tau \;[0,\;1]^T$](img369.svg)
![$\displaystyle y_h(t)=y_1(t)=[1,\;0]\;{\bf y}(t)=[1,\;0]\; e^{{\bf A}t}\int_0^t e^{-{\bf A}\tau} d\tau\; [0,\;1]^T$](img370.svg)




![$\displaystyle [1,\;0]\;\left(e^{{\bf A}t}\int_0^t e^{-{\bf A}\tau} d\tau\right)...
...1}\right)
\left({\bf I}-{\bf V}e^{-{\bf\Lambda}t}{\bf V}^{-1}\right)\;[0,\;1]^T$](img373.svg)

![$\displaystyle [1,\;0]\;{\bf V}e^{{\bf\Lambda}t} {\bf\Lambda}^{-1}{\bf V}^{-1}
-...
...Lambda}t}{\bf\Lambda}^{-1}({\bf I}-e^{-{\bf\Lambda}t} ){\bf V}^{-1}
\;[0,\;1]^T$](img374.svg)

![$\displaystyle [1,\;0]\;\left[\begin{array}{cc}1&1\\ \lambda_1&\lambda_2\end{arr...
...\\ -\lambda_1&1\end{array}\right]
\left[\begin{array}{c}0\\ 1\end{array}\right]$](img375.svg)

![$\displaystyle \left[e^{\lambda_1t},\;e^{\lambda_2t}\right]
\left[\begin{array}{...
...ac{\lambda_2e^{\lambda_1t}-\lambda_1e^{\lambda_2t}}{\lambda_2-\lambda_1}\right)$](img376.svg)




![$\displaystyle \left\{\begin{array}{l}
y'=v\\
v'=[-Ky-Cy'-K_d(y-y_d)-C_d(y'-y_d')+f]/M\\
y_d'=v_d\\
v_d'=[K_d(y-y_d)+C_d(y'-y_d')/M_d\end{array}\right.$](img380.svg)
![$\displaystyle {\bf y}'=
\left[\begin{array}{c}y'\\ v'\\ y_d'\\ v_d'\end{array}\...
...eft[\begin{array}{c}0\\ \frac{f}{M}\\ 0\\ 0\end{array}\right]
={\bf Ay}+{\bf x}$](img381.svg)
 (modeling an earthquake)
i.e.,
(modeling an earthquake)
i.e.,
![${\bf x}=[0,\;\delta(t)/M,\;0,\;0]^T$](img383.svg) , and all zero initial
condition
, and all zero initial
condition
 , then we get:
, then we get:

 as the first component of
as the first component of  is
is

 and
and  are respectively the first row
of
are respectively the first row
of  and the second column of
and the second column of
 .
.
