First and Second Order LCCODEs

Here we consider specifically solving Nth order LCCODEs with $N=1$, $N=2$, and $N=3$.

Solving first-order LCCODE:

$$y'(t)+ay(t)=x(t)$$ (37)

with an initial condition $y(t)\big\vert _{t=0}=y(0)=y_0$.

We first find the homogeneous solution, denoted by $y_h(t)$, that satisfies $y'(t)+ay(t)=x(t)=0$ due to the non-zero initial condition $y_0\ne 0$, and then find the particular solution, denoted by $y_p(t)$, that satisfies $y'(t)+a y(t)=x(t)\ne 0$. Due to the linearity of the equation, the sum $y(t)=y_h(t)+y_p(t)$ of the homogeneous and a particular solution is also a solution, called the complete solution.

To find the homogeneous solution, we assume $y(t)=c\,e^{st}$, and substitute it into the ODE to get

$$y'(t)+a\,y(t)=sc\,e^{st}+ac\,e^{st}=0$$ (38)

Dividing both sides by $c\,e^{st}\ne 0$, we get $s=-a$, i.e, $y_h(t)=c\,e^{-at}$. The coefficient $c$ is determined by the initial condition. Evaluating $y_h(t)$ at $t=0$ we get

$$y_h(t)\bigg\vert _{t=0}=c\,e^{-at}\bigg\vert _{t=0}=c=y_0$$ (39)

and the homogeneous solution is

$$y_h(t)=e^{-at} y_0$$ (40)

To find the complete solution of the nonhomogeneous ODE with $x(t)\ne 0$, we first multiply both sides of the ODE by $e^{at}$:

$$e^{at} \left[ y'(t)+a\,y(t) \right] =e^{at} y'(t)+a e^{at}y(t)=e^{at} x(t)$$ (41)

and rewrite it as

$$\frac{d}{dt} \left[ e^{at}y(t) \right]=e^{at}x(t)$$ (42)

and then integrate both sides to get

$$\int_0^t \left[\frac{d}{dt} \left( e^{a\tau}y(\tau) \right) \righ... ...e^{a\tau}y(\tau)\bigg\vert _0^t=e^{at}y(t)-y(0)=\int_0^t e^{a\tau}x(\tau) d\tau$$ (43)

Multiplying both sides by $e^{-at}$ and rearranging, we get the expression for $y(t)$

$$y(t)=e^{-at}\left[ y(0)+\int_0^t e^{a\tau}x(\tau) d\tau \right] =e^{-at}y_0+\int_0^t e^{-a(t-\tau)}x(\tau) d\tau =y_h(t)+y_p(t)$$ (44)

where $y_h(t)=e^{-at} y_0$ is the homogeneous solution same as that found above, and $y_p(t)$ is the particular solution:

$$y_p(t)=\int_0^t e^{-a(t-\tau)}x(\tau) d\tau=e^{-at}\;*\;x(t)$$ (45)

In particular, if the input $x(t)=\delta(t)$ is a unit impulse (Derac dilta function), we get the impulse response $h(t)=y_p(t)=e^{-at}$. We therefore see that in general, the particular solution is the convolution of the impulse response $h(t)=e^{-at}$ and the input $x(t)$.

Alternatively, we can also solve the first order LCCODE by the method of Laplace transform. Specifically, we take Laplace transform on both sides of the equation to get

$${\cal L}\left[ \;y'(t)+ay(t)\;\right] =sY(s)-y(0)={\cal L}\left[ \;x(t)\;\right]=X(s)$$ (46)

Solving for $Y(s)$ we get the solution in s-domain:

$$Y(s)=\frac{y_0}{s+a}+\frac{X(s)}{s+a}$$ (47)

Taking inverse transform we get the solution in time domain:

$$y(t)={\cal L}^{-1} \left[\frac{y_0}{s+a}\right] +{\cal L}^{-1}\left[ \frac{X(s)}{s+a}\right] =y_0e^{-at}+x(t)\;*\;e^{-at}$$ (48)

where $y_h(t)=y_0 e^{-at}$ is the homogeneous solution, and $y_p(t)=x(t)\,*\,e^{-at}$ as the convolution of the input $x(t)$ and the impulse response $e^{at}$ of the system is the particular solution.

• Constant input:

  Taking the unilateral Laplace transform of the equation $y'(t)+a y(t)=u(t)$ we get

  $${\cal L}\left[y'(t)+a y(t)\right]=sY(s)-y_0+aY(s) ={\cal L}\left[u(t)\right]=\frac{1}{s}$$ (49)

  Solving for $Y(s)$, we further get

  $$Y(s)=\frac{1}{s+a}\left(\frac{1}{s}+y_0\right) =\frac{y_0}{s+a}+\frac{1}{s(s+a)} =\frac{y_0}{s+a}+\frac{1}{a}\left(\frac{1}{s}-\frac{1}{s+a}\right)$$ (50)

  Taking the inverse Laplace trannsform we get the solution in time domain:

  $$y(t)={\cal L}^{-1}Y(s)=1-e^{-at}+y_0e^{-t/\tau}=1+(y_0-1)e^{-t/\tau}$$ (51)

• Sinusoidal input:

  To solve the ODE with a sinusoidal input $y'(t)+v_c(t)=x(t)=\cos(\omega t) u(t)$, we first consider a complex exponontial input

  $$y'(t)+v_c(t)=x(t)=e^{j\omega t}$$ (52)

  Taking the Laplace transform on both sides we get

  $${\cal L}\left[y'(t)+a y(t)\right]=s Y(s)-y_0+a Y(s) ={\cal L}\left[e^{j\omega t}u(t)\right]=\frac{1}{s-j\omega}$$ (53)

  Solving for $Y(s)$, we get

  $$Y(s)=\frac{1}{s+a}\left(\frac{1}{s-j\omega}+y_0\right) =\frac{1}{j\omega+a}\left(\frac{1}{s-j\omega}-\frac{1}{s+a}\right) +\frac{y_0}{s+a}$$ (54)

  Taking the inverse Laplace trannsform we get the solution in time domain:
  

  $$y(t) = {\cal L}^{-1} Y(s)=\frac{1}{j\omega+a}\left[ {\cal L}^{-1} \left(... ...}\left(\frac{1}{s+a}\right)\right] +{\cal L}^{-1}\left( \frac{y_0}{s+1} \right)$$

  $$= \frac{e^{-j\phi}}{\sqrt{\omega^2+a^2}}\left( e^{j\omega t}-e^{-at... ...}e^{j(\omega t-\phi)} -\frac{e^{-j\phi}}{\sqrt{\omega^2+a^2}}e^{-at}+y_0e^{-at}$$

  
  where $\phi=\tan^{-1}(\omega/a)$. Taking the real part we get the solution:
  

  $$y(t) = \frac{1}{\sqrt{\omega^2+a^2}}\cos(\omega t-\phi) -\frac{e^{-at}}{\sqrt{\omega^2+a^2}}\cos(-\phi)+y_0 e^{-at}$$

  $$= \frac{1}{\sqrt{\omega^2+a^2}}\cos(\omega t-\phi) +\left[y_0 -\frac{1}{\sqrt{\omega^2+a^2}}\cos(-\phi)\right] e^{-at}$$

  
  

Solving second order LCCODE:

$$y''(t)+2\zeta\omega_n y'(t)+\omega_n^2 y(t)=x(t)$$ (55)

We first find the homogeneous solution by assuming $x(t)=0$. We assume $y(t)=e^{st}$ and substitute it with its derivatives $y'(t)=s e^{st},\;y''(t)=s^2 e^{st}$ into the DE and get

$$(s^2+2\zeta\omega_n s+\omega_n^2)e^{st}=0$$ (56)

Dividing both sides by $e^{st}\ne 0$, we get an algebraic equation

$$s^2+2\zeta\omega_n s+\omega_n^2=0$$ (57)

solving which we get its two roots:

$$s_{1,2}=\left\{\begin{array}{ll} \left(-\zeta\pm\sqrt{\zeta^2-1}\... ...^2}\right)\omega_n=\omega_n e^{\mp j\phi} &\vert\zeta\vert< 1\end{array}\right.$$ (58)

where

$$\phi=\tan^{-1}\left(\frac{\sqrt{1-\zeta^2}}{\zeta}\right) =\cos^{-1}\zeta$$ (59)

and

$$\zeta+j\sqrt{1-\zeta^2}=e^{j\phi},\;\;\;\;\;\zeta-j\sqrt{1-\zeta^2}=e^{-j\phi}$$ (60)

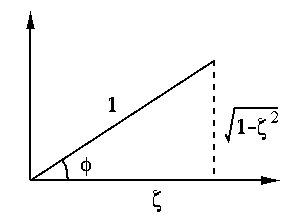
Note that

$$s_1s_2=\omega_n^2,\;\;\;\;\;\;\;\;s_1+s_2=-2\zeta\omega_n, \;\;\;\;\;\;\; s_2-s_1=-2\omega_n\sqrt{\zeta^2-1}=-2j\omega_n\sqrt{1-\zeta^2}$$ (61)

where $\omega_d$ is the damped natural frequency defined as:

$$\omega_d=\omega_n\sqrt{1-\zeta^2}$$ (62)

and

$$s^2+2\zeta\omega_n s+\omega_n^2=(s-s_1)(s-s_2)=s^2-(s_1+s_2)s+s_1s_2$$ (63)

These two roots $s_{1,2}$ are either two real numbers or a pair complex conjugate numbers, depending on whether its discriminant is greater and smaller then 0:

$$\Delta=(2\zeta\omega_n)^2-4\omega_n^2=4\omega_n^2(\zeta^2-1) \lef... ...y}{ll}\ge 0 & \vert\zeta\vert\ge 1\\ < 0 & \vert\zeta\vert< 1\end{array}\right.$$ (64)

As $\zeta\ge 0$ for all physical systems, $Re(s_1)=Re(s_2)\le 0$ for all cases.

For a constant $\omega_n$ and a variable $\zeta$ that changes from $-\infty$ to $\infty$, the two roots $s_1$ (red) and $s_2$ (blue) can be represented as the root locus on the complex plane.

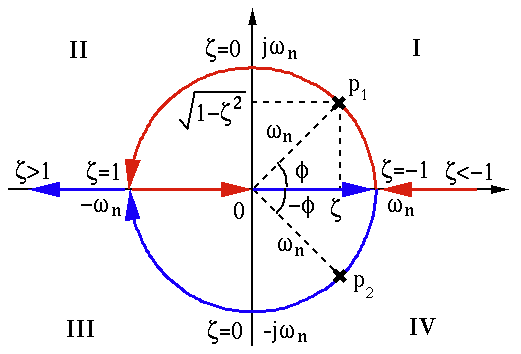
Given the two roots $s_1$ and $s_2$, we get the homogeneous solution as the linear combination of the two solutions $e^{s_1t}$ and $e^{s_2t}$:

$$y_h(t)=C_1 e^{s_1t}+C_2 e^{s_2t}$$ (65)

where the two coefficients $C_1$ and $C_2$ can be found based on the two initial conditions $y(0)=y_0$ and $y'(0)=y'_0$:

$$y(0) = y_h(t)\bigg\vert _{t=0}=C_1+C_2=y_0$$

$$\dot{y}(0) = \dot{y}_h(t)\bigg\vert _{t=0}=s_1C_1+s_2C_2=y'_0$$

Solving these we get

$$C_1=\frac{s_2y_0-y'_0}{s_2-s_1}, \;\;\;\;\;\;\;\; C_2=\frac{s_1y_0-y'_0}{s_1-s_2} y_0$$ (66)

and the homogeneous solution becomes:

$$y_h(t)=y_0 \left[ \frac{s_2 e^{s_1t}}{s_2-s_1}-\frac{s_1 e^{s_2t}}{s_2-s_1} \right] =\frac{y_0}{s_2-s_1} (s_2 e^{s_1t}-s_1 e^{s_2t})$$ (67)

The solution takes different forms depending on the value of the damping coefficient $\zeta$.

• Over-damped system ($\zeta>1$)
  

  $$y_h(t) = y_0 \left[ \frac{s_2 e^{s_1t}}{s_2-s_1}+\frac{s_1 e^{s_2t}}{s_1-s_2} \right]$$

  $$= y_0\left[\frac{-\zeta+\sqrt{\zeta^2-1}}{2\sqrt{\zeta^2-1}}e^{(-\z... ...qrt{\zeta^2-1}}{2\sqrt{\zeta^2-1}}e^{(-\zeta+\sqrt{\zeta^2-1})\omega_nt}\right]$$

  
  This is a sum of two exponentially decaying terms, without any overshoot or oscillation. Note that when $t=0$, $y_h=y_0$.

• Critically damped system ($\zeta=1$)

  Now we have

  $$s_1=s_2=-\omega_n=s$$ (68)

  and the homogeneous solution takes following form:
  

  $$y_h(t) = C_1 e^{st}+C_2 t e^{st}=C_1 e^{-\omega_nt}+C_2 t e^{-\omega_nt}$$

  $$\dot{y}_h(t) = \frac{d}{dt}[C_1 e^{st}+C_2 t e^{st}]=C_1se^{st}+C_2(e^{st}+ste^{st})$$

  
  Applying the initial conditions to this response we get
  

  $$y(0) = C_1=y_0$$

  $$\dot{y}(0) = s C_1+C_2=0$$

  
  Solving this we get

  $$C_1=y_0, \;\;\;\;\;\;\;C_2=y_0$$ (69)

  and the response is

  $$y_h(t)=C_1 e^{st}+C_2 t e^{st}=y_0\left[ e^{-\omega_nt}+\omega_n t e^{-\omega_nt}\right]$$ (70)

  Again, there is no overshoot or oscillation.
• Under-damped system ( $0 \le \zeta < 1$)

  $$s_{1,2}=(-\zeta\pm j \sqrt{1-\zeta^2})\omega_n=-\zeta\omega_n\pm j\omega_d, \;\;\;\; \;\;\;\; s_1-s_2=2j\omega_d$$ (71)

  The response is
  

  $$y_h(t) = y_0 \left[ \frac{s_2 e^{s_1t}}{s_2-s_1}-\frac{s_1 e^{s_2t}}{s_2-s_1} \right]$$

  $$= y_0\left[ \frac{(-\zeta-j\sqrt{1-\zeta^2})\omega_n}{-2j\omega_n\s... ...)\omega_n}{-2j\omega_n\sqrt{1-\zeta^2}} e^{(-\zeta\omega_n-j\omega_d)t} \right]$$

  $$= y_0\frac{e^{-\zeta\omega_nt}}{\sqrt{1-\zeta^2}} \left(\frac{e^{j\... ...j}\right) =y_0\frac{e^{-\zeta\omega_nt}}{\sqrt{1-\zeta^2}} \sin(\omega_dt+\phi)$$

  
  

• Undamped system ($\zeta =0$)

  $$s_1=j\omega_n,\;\;\;\;\;\;s_2=-j\omega_n$$ (72)

  $$y_h(t)=y_0 \left[ \frac{s_2 e^{s_1t}}{s_2-s_1}+\frac{s_1 e^{s_2t}... ...ght] =y_0\left(\frac{e^{j\omega_n}+e^{-j\omega_n}}{2}\right)=y_0\cos(\omega_nt)$$ (73)

  This result can also be obtained from the previous case:

  $$\lim_{\zeta\leftarrow 0} \left(y_0\frac{e^{-\zeta\omega_nt}}{\sqr... ...in(\omega_dt+\phi) \right) =y_0\sin(\omega_nt+\frac{\pi}{2})=y_0\cos(\omega_nt)$$ (74)

The homogeneous responses of these four cases are plotted below. Note that in all cases, $y(0)=y_0$ and $\dot{y}(0)=0$.

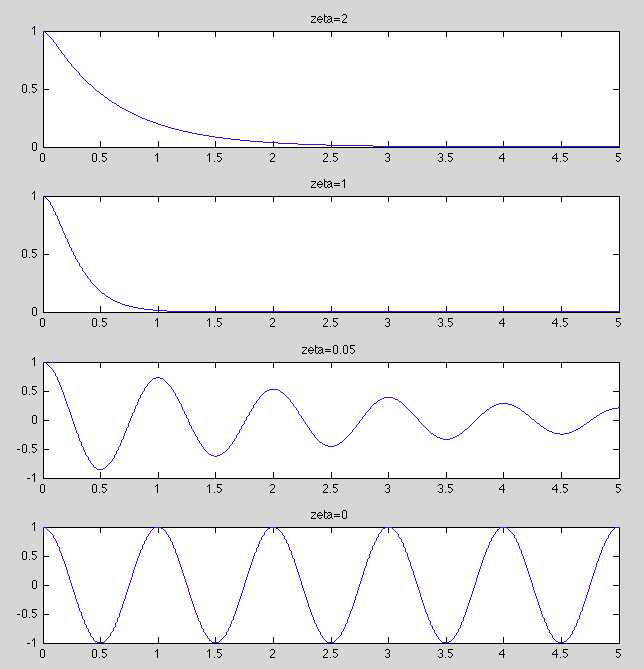
We next consider the complete solution of the equation

$$y''(t)+2\zeta\omega_n y'(t)+\omega_n^2 y(t)=x(t)$$ (75)

with a unit step $x(t)=u(t)$ input and zero initial conditions $y(0)=\dot{y}(0)=0$. As the input is a constant for $t>0$, we can assume the solution is a constant $y_p(t)=C$ with zero derivatives $y'_p(t)=y''_p(t)=0$. Substituting these into the equation, we get the particular solution (also called the steady state solution:

$$y_p(t)=\frac{1}{\omega_n^2}$$ (76)

The complete response can now be obtained as the sum of the homogeneous solution (same as that obtained previously) due to the non-zero initial condition and the particular solution due to the non-zero input:

$$y(t)=y_h(t)+y_p(t)=C_1 e^{s_1t}+C_2 e^{s_2t}+\frac{1}{\omega_n^2}$$ (77)

The two coefficients $C_1$ and $C_2$ can be obtained based on the two initial conditions, here assumed to be zero:

$$y(0) = y(t)\bigg\vert _{t=0}=C_1+C_2+\frac{1}{\omega_n^2}=0$$

$$\dot{y}(0) = \dot{y}(t)\bigg\vert _{t=0}=C_1s_1+C_2s_2=0$$

Solving these equations we get:

$$C_1=\frac{s_2}{\omega_n^2(s_1-s_2)}=\frac{-s_2}{\omega_n^2(s_2-s_1)}, \;\;\;\;\;\;C_2=\frac{s_1}{\omega_n^2(s_2-s_1)}$$ (78)

Now the complete solution becomes:

$$y(t)=\frac{1}{\omega_n^2}\left[1-\left(\frac{s_2e^{s_1t}}{s_2-s_1... ...ht] =\frac{1}{\omega_n^2}\left[1-\frac{s_2e^{s_1t}-s_1e^{s_1t}}{s_2-s_1}\right]$$ (79)

The two roots $s_1$ and $s_2$ take different forms depending on whether the discriminant $\Delta=4\omega_n^2(\zeta^2-1)$ is greater or smaller than 0, i.e., whether $\zeta$ is greater or smaller then 1. Here we only consider the case when $0 < \zeta < 1$, i.e., $\Delta<0$, for an under-damped second order system. The two roots are

$$s_{1,2}=\omega_n \; (-\zeta\pm j\sqrt{1-\zeta^2})=-\zeta \omega_n\pm j\omega_d, \;\;\;\; \;\;\;\;s_2-s_1=-2j\omega_d$$ (80)

where $\omega_d$ is the damped natural frequency:

$$\omega_d=\omega_n\sqrt{1-\zeta^2}$$ (81)

Finally the complete solution of the non-homogeneous DE is:

$$y(t) = \frac{1}{\omega_n^2}\left[1-\left(\frac{s_2}{s_2-s_1}e^{s_1t}-\frac{s_1}{s_2-s_1}e^{s_2t}\right)\right]$$

$$= \frac{1}{\omega_n^2}\left[ 1- \left(\frac{\zeta+j\sqrt{1-\zeta^2}... ...1-\zeta^2}}{2j\sqrt{1-\zeta^2}} e^{(-\zeta\omega_n-j\omega_d)t} \right) \right]$$

$$= \frac{1}{\omega_n^2}\left[ 1-\frac{e^{-\zeta\omega_nt}}{\sqrt{1-\... ...j\omega_dt} -\frac{\zeta-j\sqrt{1-\zeta^2}}{2j} e^{-j\omega_dt} \right) \right]$$

$$= \frac{1}{\omega_n^2}\left[ 1-\frac{e^{-\zeta\omega_nt}}{\sqrt{1-\... ...rac{ e^{j\phi} e^{ j\omega_dt}-e^{-j\phi} e^{-j\omega_dt} }{2j} \right) \right]$$

$$= \frac{1}{\omega_n^2}\left[1-\frac{e^{-\zeta\omega_nt}}{\sqrt{1-\zeta^2}} \sin(\omega_dt+\phi) \right]$$

where $\phi=\tan^{-1}( \sqrt{1-\zeta^2}/\zeta )$ same as that given above. In particular, if $\zeta =0$, we have

$$y(t)=\frac{1}{\omega_n^2}\left[1-\sin(\omega_n t+\pi/2)\right] =\frac{1}{\omega_n^2}\left[1-\cos(\omega_n t)\right]$$ (82)

The plots below shows an example with $f_n=1, \omega_n=2\pi$. Note the critical damped case when $\zeta=1$. An overshoot will occur for any $\zeta<1$.

The step response is plotted below. Note that $y(0)=0$ and $\dot{y}(0)=0$.

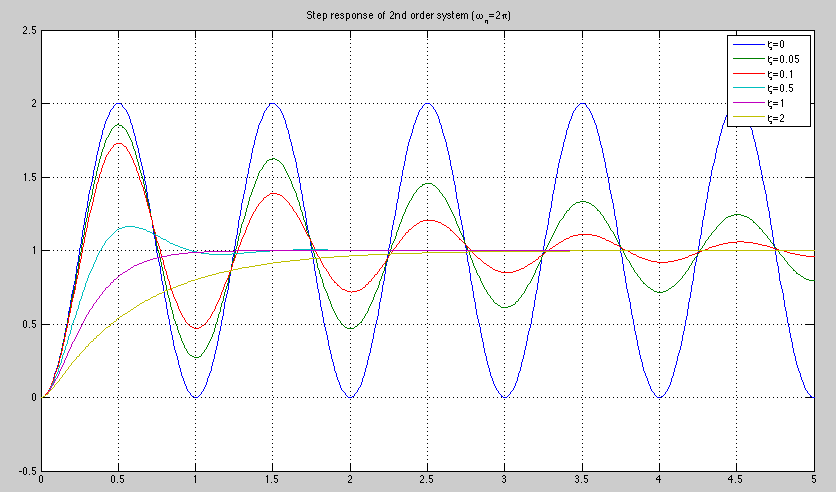
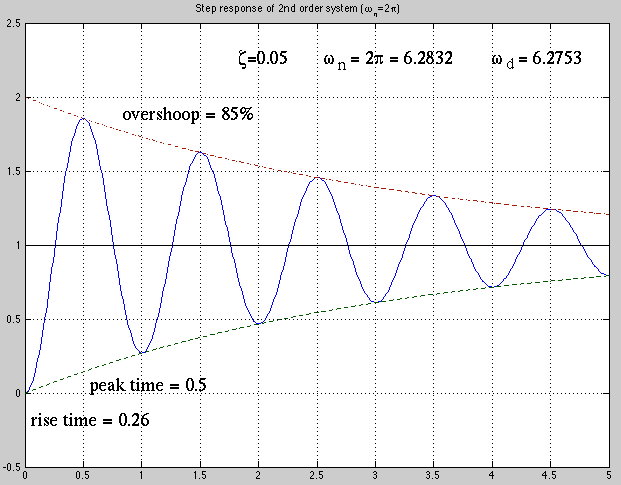
Alternatively, we can also solve the second order LCCODE by the method of Laplace transform. Specifically, we take Laplace transform on both sides of the equation to get

$${\cal L}\left(y''+2\zeta\omega_ny'+\omega_n^2y\right) =s^2Y(s)-sy(0)-y'(0)+2\zeta\omega_nY(s)-2\zeta\omega_ny(0)+\omega_n^2Y(s) =X(s)$$ (83)

Dividing both sides by $s^2+2\zeta\omega_ns+\omega_n^2=(s-s_1)(s-s_2)$ and rearranging, we get

$$Y(s)=\frac{X(s)}{(s-s_1)(s-s_2)}+\frac{(s+2\zeta\omega_n)y(0)}{(s-s_1)(s-s_2)} +\frac{y'(0)}{(s-s_1)(s-s_2)}$$ (84)

• Homogeneous case:

  If we assume $y(0)=y_0$ and $y'(0)=0$, then the above becomes

  $$Y(s)=\frac{(s+2\zeta\omega_n)y_0}{(s-s_1)(s-s_2)} =\frac{C_1}{s-s_1}+\frac{C_2}{s-s_2} =\frac{C_1(s-s_2)+C_2(s-s_1)}{(s-s_1)(s-s_2)}$$ (85)

  i.e.,

  $$C_1+C_2=y_0,\;\;\;\;\;\;s_2C_1+s_1C_2=-2\zeta\omega_n y_0=(s_1+s_2)y_0$$ (86)

  Solving for $A$ and $B$ we get

  $$C_1=\frac{s_2}{s_2-s_1}y_0,\;\;\;\;C_2=\frac{-s_1}{s_2-s_1}y_0$$ (87)

  and

  $$y(t)={\cal L}^{-1}Y(s)={\cal L}\left(\frac{C_1}{s-s_1}+\frac{C_2}... ..._1e^{s_1t}+C_2e^{s_2t} =\frac{y_0}{s_2-s_1}\left(s_2e^{s_1t}-s_1e^{s_2t}\right)$$ (88)

• Impulse response:

  If we assume $x(t)=\delta(t)$ with $X(s)={\cal L}[ \delta(t) ]=1$ and zero initial condition $y(0)=y'(0)=0$, then the transfer function is

  $$H(s)=Y(s)=\frac{1}{(s-s_1)(s-s_2)} =\frac{1}{s_2-s_1}\left( \frac{1}{s-s_2}-\frac{1}{s-s_1}\right)$$ (89)

  and the impulse response function is

  $$h(t)={\cal L}^{-1}[H(s)]=\frac{1}{s_2-s_1} {\cal L}^{-1}\left( \f... ...-s_2}-\frac{1}{s-s_1}\right) =\frac{1}{s_2-s_1}\left( e^{s_2t}-e^{s_1t} \right)$$ (90)

  Alternatively, we can also find $h(t)$ as
  

  $$h(t) = e^{s_1t}\;*\;e^{s_2t}=\int_0^t e^{s_1(t-\tau} e^{s_2\tau}\;d\tau ... ...s_2-s_1)\tau}\;d\tau =\frac{e^{s_1t}}{s_2-s_1} e^{(s_2-s_1)\tau}\bigg\vert _0^t$$

  $$= \frac{e^{s_1t}}{s_2-s_1} \left(e^{(s_2-s_1)t}-1\right) =\frac{1}{s_2-s_1}\left( e^{s_2t}-e^{s_1t}\right)$$ (91)

  
  Substituting in $s_{1,2}=(-\zeta\pm j\sqrt{1-\zeta^2})\omega_n =-\zeta\omega_n\pm \omega_d$, we further get
  

  $$h(t) = \frac{1}{s_2-s_1}\left( e^{s_2t}-e^{s_1t}\right) =\frac{1}{-2j\om... ...2}\right)\omega_nt} -e^{\left(-\zeta+j\sqrt{1-\zeta^2}\right)\omega_nt} \right)$$

  $$= \frac{e^{-\zeta\omega_nt}}{\omega_d}\sin(\omega_dt)\;\;\;\;\;\;\;(t>0)$$ (92)

  
  

• Nonhomogeneous case:

  If we assume $x(t)=u(t)$ with $X(s)={\cal L}[ u(t) ]=1/s$ and zero initial condition $y(0)=y'(0)=0$, then we have
  

  $$Y(s) = \frac{X(s)}{(s-s_1)(s-s_2)}=\frac{1}{s(s-s_1)(s-s_2)} =\frac{C_1}{s}+\frac{C_2}{s-s_1}+\frac{C_3}{s-s_2}$$

  $$= \frac{(s-s_1)(s-s_2)C_1+s(s-s_2)C_2+s(s-s_1)C_3}{s(s-s_1)(s-s_2)}$$ (93)

  
  i.e.,

  $$(C_1+C_2+C_3)s^2=0,\;\;\;\;\;\;(s_1+s_2)C_1+s_2C_2+s_1C_3=0,\;\;\;\;\;\; s_1s_2 C_1=1$$ (94)

  Solving for $A$, $B$ and $C$ we get

  $$C_1=\frac{1}{s_1s_2}=\frac{1}{\omega_n^2},\;\;\;\;\; C_2=\frac{1}... ...n^2}\frac{-s_2}{s_2-s_1},\;\;\;\;\; C_3=\frac{1}{\omega_n^2}\frac{s_1}{s_2-s_1}$$ (95)

  and

  $$y(t)={\cal L}^{-1}\left( \frac{C_1}{s}+\frac{C_2}{s-s_1}+\frac{C_... ...t} =\frac{1}{\omega_n^2}\left( 1-\frac{s_2e^{s_1t}-s_1e^{s_2t}}{s_2-s_1}\right)$$ (96)

  As shown above, when $0 < \zeta < 1$, we have

  $$y(t)=\frac{1}{\omega_n^2}\left[1-\frac{e^{-\zeta\omega_nt}}{\sqrt{1-\zeta^2}} \sin(\omega_dt+\phi) \right]$$ (97)

  Alternatively, the same step response can also be found as the convolution of the impulse response $h(t)$ and the input $x(t)=u(t)$:
  

  $$y(t) = h(t)\;*\;u(t)=\int_{-\infty}^\infty h(\tau) u(t-\tau)\;d\tau =\in... ...tau =\frac{1}{\omega_d}\int_0^t e^{-\zeta\omega_n\tau}\sin(\omega_d\tau)\;d\tau$$

  $$= \frac{1}{\omega_n\sqrt{1-\zeta^2}} \left[\frac{e^{-\zeta\omega_n\... ...(-\zeta\omega_n\sin(\omega_d\tau)-\omega_d\cos(\omega_d\tau)\right) \right]_0^t$$

  $$= \frac{1}{\sqrt{1-\zeta^2}} \left[ \frac{e^{-\zeta\omega_n\tau}}{(... ...t(-\zeta\sin(\omega_d\tau)-\sqrt{1-\zeta^2}\cos(\omega_d\tau)\right)\right]_0^t$$

  $$= \frac{e^{-\omega_n\tau}}{\omega_n^2\sqrt{1-\zeta^2}} \left( \cos\... ...omega_n\tau}}{\omega_n^2\sqrt{1-\zeta^2}}\sin(\omega_d\tau+\phi)\bigg\vert _t^0$$

  $$= \frac{1}{\omega_n^2\sqrt{1-\zeta^2}}\left[ \sin\phi-e^{-\zeta\omega_nt}\sin(\omega_dt+\phi)\right]$$

  $$= \frac{1}{\omega_n^2}\left[1-\frac{e^{-\zeta\omega_nt}}{\sqrt{1-\zeta^2}} \sin(\omega_dt+\phi) \right]$$ (98)

  
  where we have used the facts that $\sin\phi=\sqrt{1-\zeta^2}$ and $\omega_d=\omega_n\sqrt{1-\zeta^2}$, and the integral

  $$\int e^{at}\sin(bt)\;dt=\frac{e^{at}}{a^2+b^2}\left[ a\sin(bt)-b\cos(bt)\right]$$ (99)

Solving third order LCCODE:

$$y'''(t)+a_2 y''(t)+a_1 y'(t) + a_0y(t)=x(t)$$ (100)

with initial conditions $y^{(n)}(0)=y^{(n)}_0,\;(n=0,\cdots,2)$. Here we only consider the Homogeneous case. Let $s_1,\,s_2,\,s_3$ be the three roots of the characteristic equation so that

$$s^3+a_2 s^2+a_1 s +a_0=(s-s_1)(s-s_2)(s-s_3)$$

$$= s^3-(s_1+s_2+s_3) s^2+(s_1s_2+s_2s_3+s_1s_3)s-s_1s_2s_3 =0$$ (101)

i.e, $a_2=-(s_1+s_2+s_3)$, $a_1=s_1s_2+s_2s_3+s_1s_3$ and $a_0=-s_1s_2s_3$. We let $y(t)=C_1 e^{s_1t}+C_2 e^{s_2t}+C_3 e^{s_3t}$, and find the coefficients ${\bf c}=[c_1,\;c_2,\;c_3]^T$ by solving the equation

$${\bf Sc}=\left[\begin{array}{ccc}1 & 1 & 1\\ s_1 & s_2 & s_3\\ s... ...ray}\right] =\left[\begin{array}{c}y_0\\ y'_0\\ y''_0\end{array}\right]={\bf y}$$ (102)

to get ${\bf c}={\bf S}^{-1}{\bf y}$, where

$${\bf S}^{-1}=\left[\begin{array}{ccc} 1 & 1 & 1\\ s_1 & s_2 & s_3... ... s_1s_3 & -(s_1+s_3) & 1\\ s_1s_2 & -(s_1+s_2) & 1 \end{array}\right] ={\bf DR}$$ (103)

Alternatively, we can use the method of Laplace transform to get

$$Y_h(s) = \frac{ (y_0s^2+y'_0s+y''_0) +a_2(y_0s+y'_0)+a_1y_0}{(s-s_1)(s-s_2)(s-s_3)} =\frac{c_1}{s-s_1}+\frac{c_2}{s-s_2}+\frac{c_3}{s-s_3}$$

$$= \frac{c_1(s^2-(s_2+s_3)s+s_2s_3)+c_2(s^2-(s_1+s_3)s+s_1s_3)+c_3(s^2-(s_1+s_2)s+s_1s_2)} {(s-s_1)(s-s_2)(s-s_3)}$$ (104)

Equating the coefficients for $s^2,\;s$ and constant terms of the numerators, we get

$$\left[\begin{array}{ccc} s_2s_3 & s_1s_3 & s_1s_2\\ -(s_2+s_3) & ... ... \end{array}\right] \left[\begin{array}{c} y_0\\ y'_0\\ y''_0\end{array}\right]$$ (105)

which can be written as

$${\bf R}^T{\bf c}={\bf Ay},\;\;\;\;\; \;\;\;\;\; {\bf c}=({\bf R}^T)^{-1}{\bf Ay}$$ (106)

But we also note the following identity:

$${\bf AS}=\left[\begin{array}{ccc} a_1 & a_2 & 1\\ a_2 & 1 & 0\\ 1... ...s_1s_2\\ -(s_2+s_3)&-(s_1+s_3)&-(s_1+s_2)\\ 1&1&1\end{array}\right] ={\bf R}^T$$ (107)

i.e., $({\bf R}^T)^{-1}={\bf S}^{-1}{\bf A}^{-1}$. Substituting this into the expression for ${\bf c}$ we get the same coefficients found previously:

$${\bf c}=({\bf R}^T)^{-1}{\bf Ay}={\bf S}^{-1}{\bf A}^{-1}{\bf Ay}={\bf S}^{-1}{\bf y}$$ (108)