Next: Nelder-Mead method Up: Unconstrained Optimization Previous: Golden section search
If a function 



 |
(17) |
 at the vertex of this quadratic function,
we first set its derivative to zero:
at the vertex of this quadratic function,
we first set its derivative to zero:
 |
(18) |
 :
:
 |
|||
 |
![$\displaystyle 2x[f(a)(c-b)+f(b)(a-c)+f(c)(b-a)]
-[f(a)(c^2-b^2)+f(b)(a^2-c^2)+f(c)(b^2-a^2)]=0$](img104.svg) |
(19) |
 to get:
to get:
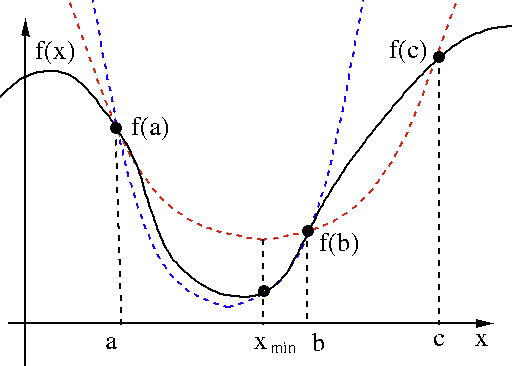
 is already at the vertex of
is already at the vertex of  ,
,
 is smaller than
is smaller than
 , i.e.,
, i.e.,  is closer to the minimum of
is closer to the minimum of  than
than  . This
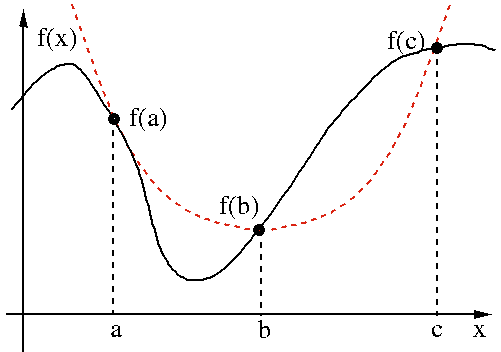
interpolation process can then be repeated using a set of three new points
of
. This
interpolation process can then be repeated using a set of three new points
of
 if
if  or
or
 if
if  .
.
In the unlikely case where the numerator of the second term in
Eq. (20) is zero, i.e.,
^2=[f(c)-f(b)](b-a)^2$](img118.svg)