Golden section search

The golden section search algorithm can be used for finding a minimum (or maximum) of a single-variable function $f(x)$. If it is known that the function has a minimum between some two points, then we can search for it iteratively, in a manner similar to the bisection search for the root of an equation $f(x)=0$. Specifically, if in the neighborhood of the minimum we can find three points $x_0<x_1<x_2$ corresponding to $f(x_0)>f(x_1)<f(x_2)$, then there exists a minimum between $x_0$ and $x_2$. To search for this minimum, we can choose another point $x_3$ between $x_1$ and $x_2$ as shown in the figure below, with the following two possible outcomes:

• If $f(x_3)=f_{3a}>f(x_1)$, the minimum is inside the interval $x_3-x_0=a+c$ associated with three new points $x_0<x_1<x_3$, i.e., $x_2$ is replaced by $x_3$.
• If $f(x_3)=f_{3b}<f(x_1)$, the minimum is inside the interval $x_2-x_1=b$ associated with three new points $x_1<x_3<x_2$, i.e., $x_0$ is replaced by $x_1$.

In either case, the new search interval $x_3-x_0=a+c$ or $x_2-x_1=b$ is smaller than the old one $x_2-x_0=a+b$, i.e., such an iteration is guaranteed to converge. Of course $x_3$ can also be between $x_0$ and $x_1$, the iteration can be similarly carried out accordingly.

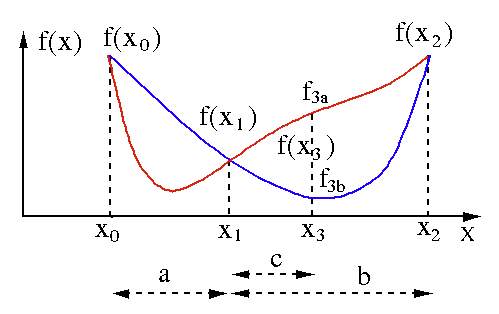
Similar to the bisection search for the root of $f(x)=0$, here to search for the minimum of $f(x)$, we also want to avoid the worst possible case in which the minimum always happens to be in the larger one of the two sections $a+c$ and $b$. We therefore choose $x_3$ in such a way that the two resulting search intervals will always be the same:

$$a+c=b,\;\;\;\;\;\;\; \;\;\;\;\;\;\;c=b-a$$ (10)

In other words, through out the iteration, the search interval should always be partitioned into two sections with the same ratio:

$$\frac{a+b}{b}=\frac{a+c}{a}=\frac{b}{a} \;\;\;\;\; \;\;\;\;\; \frac{a+b}{b}=\frac{b}{b-c}=\frac{b}{a}$$ (11)

In either case, we get

$$a^2+ab-b^2=0$$ (12)

Solving this quadratic equation for $a$ in terms of $b$ we get

$$a_{1,2}=\frac{-1\pm\sqrt{5}}{2}\;b =\left\{\begin{array}{r}0.618\,b\\ -1.618\,b\end{array}\right.$$ (13)

We keep the positive result and get

$$\frac{a}{b}=0.618,\;\;\;\;\;\;\;\;\; \frac{b}{a+b}=\frac{b}{0.618b+b}=\frac{1}{1.618}=0.618$$ (14)

This is the golden ratio between the two sections $a$ and $b$ of the search interval.

The iteration of the golden section search can terminate when the size of the search brackets $\vert x_2-x_0\vert$ is small enough, compared with some tolerance, such as $10^{-9}$, pre-determined based on some prior knowledge of the scale of the problem. However, this scale may be unknown, or it may vary drastically, and an absolute tolerance may be too large for a small scale problem but too small for a large scale problem. This problem can be resolved by using a relative tolerance with a scale comparable with that of the size of the problem:

$$\vert x_2-x_0\vert < \epsilon(\vert x_1\vert+\vert x_3\vert)$$ (15)

where $\epsilon$ is a small value such as $10^{-9}$, and $\vert x_2-x_0\vert$ represents the size of the search interval and $\vert x_1\vert+\vert x_3\vert$ represents the scale of the problem. When the inequality is satisfied, the iteration is terminated.

It is possible that the three initial points chosen are such that either $f(x_0)<f(x_1)<f(x_2)$ or $f(x_0)>f(x_1)>f(x_2)$, then we have to search toward the descending direction of $f(x)$ until it starts to ascend. For example, if $f(x_0)>f(x_1)>f(x_2)$, they can be iteratively updated by the following

$$x^{new}_0=x^{old}_1,\;\;\;\;x^{new}_1=x^{old}_2, \;\;\;\;x^{new}_2=x^{old}_2+c(x^{old}_2-x^{old}_1)$$ (16)

where $c>1$ (e.g., $c=1.618$), until we reach a point $x_2$ at which $f(x_2)>f(x_1)$. Obviously the distance $d=x_2-x_1$ grows exponentially $d\propto c^n$.