Hopfield Network

The Hopfield network is a supervised method, based on the Hebbian learning rule. As a supervised method, the Hopfield network is trained based on a set of $K$ patterns in dataset ${\bf X}=[{\bf x}_1,\cdots,{\bf x}_K]$, where each data point ${\bf x}_k=[x_1,\cdots,x_d]^T$ is a d-dimensional binary vector containing $x_i \in\{-1,\;1\},\;(i=1,\cdots,d)$, representing one of $K$ different of patterns of interest. Once the network is completely trained, a weight matrix ${\bf W}$ of the network is obtained in which the $K$ patterns are stored. Given an input ${\bf x}$, an iterative computation is carried out until convergence, when one of the pre-stored complete pattern that most closely resemble the input ${\bf x}$ is produced as the output. The Hopfield network can therefore be considered as an auto-associator (a content addressable memory), by which a pre-stored pattern can be retrieved based on its association to the input pattern established by the network.

Structurally, the Hopfield network is a recurrent network, in the sense that the outputs of its single layer of $d$ nodes are fed back to these nodes in an iterative process.

• Training:

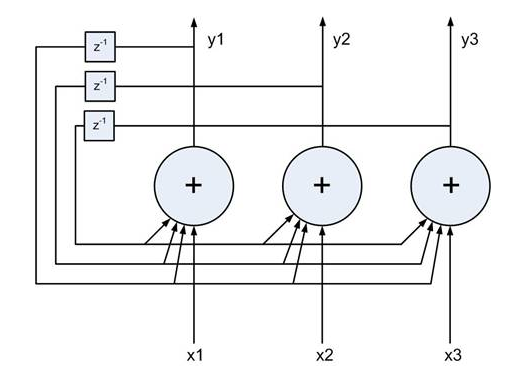
  The training process is essentially the same as the Hebbian learning, except here the two associated patterns in each pair are the same (self-association). The weight matrix of the network is obtained as the sum of the outer-products of the $K$ patterns to be stored:

  $${\bf W}_{d\times d}=\frac{1}{d}\sum_{k=1}^K {\bf x}_k {\bf x}_k^T... ...k)} \\ \vdots \\ x_d^{(k)} \end{array} \right] [ x_1^{(k)}, \cdots, x_d^{(k)} ]$$ (20)

  The weight connecting node i and node j is defined as

  $$w_{ij}=\frac{1}{d}\sum_{k=1}^K x_i^{(k)} x_j^{(k)}=w_{ji}$$ (21)

  We assume no self-connection exists $w_{ii}=0\;(i=1,\cdots,d)$

• Autoassociation:

  Once the weight matrix ${\bf W}$ is obtained by the training process, the network can be used as a self-associator. When an input pattern ${\bf x}$ is presented to the network, the outputs of the network are updated iteratively and asynchronously, one randomly selected node at a time:

  $$x_i^{(n+1)}=sgn \left(\sum_{j=1}^d w_{ij}x_j^{(n)}\right) =\left\... ...0 \\ -1, & \mbox{if}\;\;\;\sum_{j=1}^d w_{ij}x_j^{(n)} < 0 \end{array} \right.$$ (22)

  where $x_i^{(n)}$ and $x_i^{(n+1)}$ are the output $x_i$ of the ith node before and after the nth iteration, respectively. As shown below, this iteration will always converge to one of the $K$ pre-stored patterns.

We first define the Energy function of any two nodes $x_i$ and $x_j$ of ${\bf x}$ as

$$e_{ij}=-w_{ij}x_ix_j$$ (23)

and the total energy of all $d$ nodes in the network as the sum of all pair-wise energies:

$${\cal E}({\bf x}) = \frac{1}{2}\sum_{i=1}^d\sum_{j=1}^d e_{ij} =-\frac{1}{2}\sum_{i=1}^d \sum_{j=1}^d w_{ij} x_i x_j =-\frac{1}{2}{\bf x}^T{\bf Wx}$$ (24)

The interaction between these two nodes is summarized below:

$$\begin{tabular}{ c \vert r \vert r \vert\vert c \vert c} \hline &... ...e_{ij}<0$ \\ \hline 4 & 1 & 1 & $e_{ij}<0$ & $e_{ij}>0$ \\ \hline \end{tabular}$$ (25)

We make two observations.

• When the two nodes i and j reinforce each other's state, $e_{ij}<0$:
  • If $w_{ij}>0$ (in cases 1 and 4), $x_j=\mp 1$ tends to keep $x_i$ to stay at the same state $\mp 1$ in the iteration.

  • If $w_{ij}<0$ (in cases 2 and 3), $x_j=\mp 1$ tends to keep $x_i$ to stay at the same state $\pm 1$.

• When the two nodes i and j change each other's state, $e_{ij}>0$:
  • If $w_{ij}<0$ (in cases 1 and 4), $x_j=\mp 1$ tends to reverse $x_i$ from its previous state $\mp 1$ to $\pm 1$.

  • If $w_{ij}>0$ (in cases 2 and 3), $x_j=\mp 1$ tends to reverse $x_i$ from its previous state $\pm 1$ to $\mp 1$.

We note that low energy $e_{ij}$ corresponds to a stable interaction between $x_i$ and $x_j$, i.e., they tend to remain unchanged, and high energy corresponds to an unstable interaction, i.e., they tend to change their states. As the result, low total ${\cal E}({\bf x})$ corresponds to more stable condition of the network, while high ${\cal E}({\bf x})$ corresponds to less stable condition.

We further show that the total energy ${\cal E}({\bf x})$ always decreases whenever the state of any node changes. Assume $x_k$ has just been changeed, i.e., $x_k^{(n+1)} \neq x_k^{(n)}$ ($x_k=\pm 1$ but $x_k^{(n+1)}=\mp 1$), while all others remain the same $x_{l \neq k}^{(n+1)}=x_{l \neq k}^{(n)}$. The energy before $x_k$ changes state is

$${\cal E}^{(n)}({\bf x}) = -\frac{1}{2} \left[ \sum_{i\neq k}\sum_{j\neq k}w_{ij}x_i^{(n)}x_j^{(n)} +\sum_i w_{ik}x_i^{(n)}x_k^{(n)}+\sum_j w_{kj}x_k^{(n)}x_j^{(n)} \right]$$

$$= -\frac{1}{2} \sum_{i\neq k}\sum_{j\neq k}w_{ij}x_ix_j - \sum_i w_{ik}x_i^{(n)}x_k^{(n)}$$

and the energy after $x_k$ changes state is

$${\cal E}^{(n+1)}({\bf x})= -\frac{1}{2} \sum_{i\neq k}\sum_{j\neq k}w_{ij}x_ix_j - \sum_i w_{ik}x_i^{(n+1)}x^{(n+1)}_k$$ (26)

The energy difference is

$$\bigtriangleup {\cal E}=(x_k^{(n)}-x_k^{(n+1)}) \sum_i w_{ik}x_i$$ (27)

Consider two cases:

• Case 1: if $x_k^{(n)}=-1$, but $\sum_i w_{ik}x_i \geq 0$ and $x_k^{(n+1)}=1$, we have $(x_k^{(n)}-x_k^{(n+1)})=-2 \le 0$ and $\bigtriangleup {\cal E} \leq 0$.
• Case 2: if $x_k^{(n)}=1$, but $\sum_i w_{ik}x_i < 0$ and $x_k^{(n+1)}=-1$, we have $(x_k^{(n)}-x_k^{(n+1)})=2 \ge 0$ and $\bigtriangleup {\cal E} \leq 0$.

As in either case, $\bigtriangleup {\cal E}({\bf x}) \leq 0$ is always true throughout the iteration, we conclude that ${\cal E}({\bf x})$ will eventually reach one of the minima of the energy landscape, i.e., the iteration will always converge.

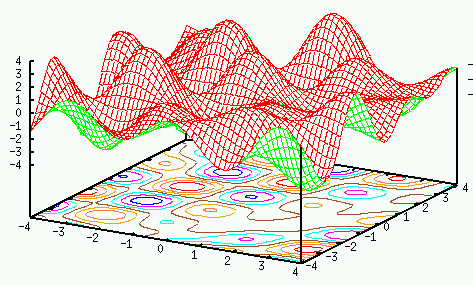
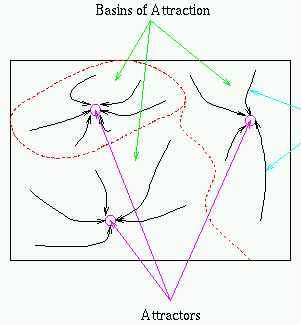
We further show that each one of the $K$ pre-stored patterns corresponds to one of the minima of the energy function. The energy function ${\cal E}({\bf x})$ corresponding to any ${\bf x}$ can be written as

$${\cal E}({\bf x}) = -\frac{1}{2}{\bf x}^T{\bf Wx} =-\frac{1}{2}{\... ...^T{\bf x}_k{\bf x}_k^T{\bf x} =-\frac{1}{2d}\sum_{k=1}^K ({\bf x}^T{\bf x}_k)^2$$ (28)

If ${\bf x}$ different (ideally orthogonal to) from any of the stored patterns, all $K$ terms of the summation will be small (ideally zero). But if ${\bf x}$ is the same as any one of the stored patterns, their inner product reaches maximum, causing the total energy to be minimized to reach one of the minima. In other words, the patterns stored in the network correspond to the local minima of the energy function. i.e., these patterns become attractors.

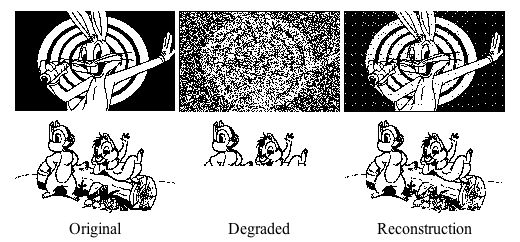
Note that it is possible to have other local minima, called spurious states, which do not represent any of the stored patterns, i.e., the associative memory is not perfect.