Hebbian Learning

Donald Hebb (1949) speculated that “When neuron A repeatedly and persistently takes part in exciting neuron B, the synaptic connection from A to B will be strengthened.” In other words, simultaneous activation of neurons leads to pronounced increases in synaptic strength between them, or “neurons that fire together wire together; neurons that fire out of sync, fail to link".

For example, the well known classical conditioning (Pavlov, 1927) could be explained by Hebbian learning. Consider the following three patterns (see here):

• Unconditioned stimulus: sight of food F
• Conditioned stimulus: sound of bell B
• Response: salivation S

The unconditioned response is: $F \rightarrow S$. Due to the repeated and persistent conditioning process $F \cap B \rightarrow S$, the synaptic connections between patterns B and S are strengthened as both are repeatedly excited simultaneously, i.e., the two patterns become associated, resulting the conditioned response $B \rightarrow S$.

Based on this theory of Hebbian learning, the Hebbian network can be considered as a supervised learning method that learns to establish the associative relationship between any pair of two patterns ${\bf x}_n$ and ${\bf y}_n$ in the given dataset $\{{\bf x}_1,\cdots,{\bf x}_N\}$ and $\{{\bf y}_1,\cdots,{\bf y}_N\}$, considered as the training set. This is a 2-layer network with $d$ nodes in the input layer to receive an input pattern ${\bf x}=[x_1,\cdots,x_d]^T$ and $m$ nodes in the output layer to produce an output ${\bf y}=[y_1,\cdots,y_m]^T$. Each output node is fully connected to all $d$ input nodes through its weights:

$$y_i=\sum_{j=1}^d w_{ij} x_j={\bf w}_i^T{\bf x}\;\;\;\;(i=1,\cdots,m)$$ (11)

where ${\bf w}_i=[w_{i1},\cdots,w_{id}]^T$, or in matrix form

$${\bf y}=\left[\begin{array}{c}y_1\\ \vdots\\ y_m\end{array}\right... ...ght] \left[\begin{array}{c}x_1\\ \vdots\\ x_d\end{array}\right] ={\bf W}{\bf x}$$ (12)

where ${\bf W}=[{\bf w}_1,\cdots,{\bf w}_m]^T$ is an $m\times d$ matrix.

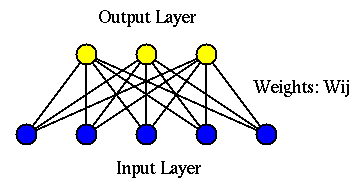
The Hebbian learning rule is inspired by Hebb's theory, i.e., when both neurons $x_j$ and $y_i$ are activated, the synaptic connectivity, here the weight $w_{ij}$, between them is enhanced:

$$w_{ij}^{new}=w_{ij}^{old}+\eta\;x_j y_i\;\;\;\;(i=1,\cdots,m,\;j=1,\cdots,d)$$ (13)

or in matrix form:

$${\bf W}^{new}={\bf W}^{old}+\eta\; {\bf y} {\bf x}^T$$ (14)

Here $\eta$ is the learning rate, a parameter that controls how quickly the weights get modified.

As in all supervised learning, the Hebbian network is first trained and then used for association.

• Training:

  For simplicity, we assume all weights are initialized to zero $w_{ij}=0\;\;\;\;(i=1,\cdots,m,\;j=1,\cdots,d)$, and then train the network to find all weights based on all $N$ pattern pairs in the dataset $\{ ({\bf x}_n,{\bf y}_n),\;\;n=1,\cdots,N\}$ based on the learning law:

  $$w_{ij}=\sum_{n=1}^N x_j^{(n)}y_i^{(n)} \;\;\;\;(i=1,\cdots,m,\;\;j=1,\cdots,d)$$ (15)

  or in matrix form, the weight matrix is the sum of the outer-products of all $N$ pairs of patterns:

  $${\bf W}_{m\times d}=\sum_{n=1}^N {\bf y}_n {\bf x}_n^T = \sum_{n=... ...n)} \\ \vdots \\ y_m^{(n)} \end{array} \right] [ x_1^{(n)}, \cdots, x_d^{(n)} ]$$ (16)

• Association:

  When one of the patterns ${\bf x}_l$ is presented to the network, it produces an output:

  $${\bf y}={\bf W}{\bf x}_l$$ (17)

  which, as shown below, is the same as the associated pattern ${\bf y}_l$, under the following conditions:
  • The $N$ patterns $\{{\bf x}_1,\cdots,{\bf x}_N\}$ are treated as zero-mean random vectors, and they are assumed to be completely uncorrelated with zero correlation coefficient between any ${\bf x}_i$ and ${\bf x}_j$:

    $$r_{ij}=\frac{\sigma_{ij}^2}{\sigma_i\sigma_j} =\frac{\sum_{k=1}^d... ...\delta_{ij} =\left\{ \begin{array}{ll} 1 & i=j \\ 0 & i\ne j \end{array}\right.$$ (18)

    If we further assume all patterns are normalized with $\vert\vert{\bf x}_n\vert\vert=1$, then we have ${\bf x}_i^T{\bf x}_j=\delta_{ij}$

  • The number of input nodes is greater than the number of pattern pairs: $d \geq N$, i.e., the capacity of the network is large enough for representing $N$ different patterns (as there can be no more than $d$ orthogonal vectors in a d-dimensional space).

  Under these conditions, the output of the network as its response to input ${\bf x}_l$ is

  $${\bf y}={\bf W}{\bf x}_l =\left(\sum_{n=1}^N {\bf y}_n {\bf x}_n^... ...({\bf x}_l^T{\bf x}_l) +\sum_{n\neq l}{\bf y}_n({\bf x}_n^T{\bf x}_l)={\bf y}_l$$ (19)

  as ${\bf x}_n^T {\bf x}_l=0$ for all other terms with $n \ne l$. We see that a one-to-one correspondence relationship between ${\bf x}_n$ and ${\bf y}_n$ has been established for all $n=1,\cdots,N$. In non-ideal cases when the conditions above are not fully satisfied, the summation term is non-zero and there is an error ${\bf y}-{\bf y}_l \neq 0$.