Next: Hebbian Learning Up: ch10 Previous: ch10
In machine learning, the artificial neural networks are a category of algorithms that are inspired by the biological neural networks in the brain, and designed to carry out both supervised and unsupervised learning tasks, such as classification and clustering. To understand how such neural network algorithms work, we first consider some basic concepts in biological neural system.
The human brain consists of 


Functionally, a neuron consists of the following three parts:
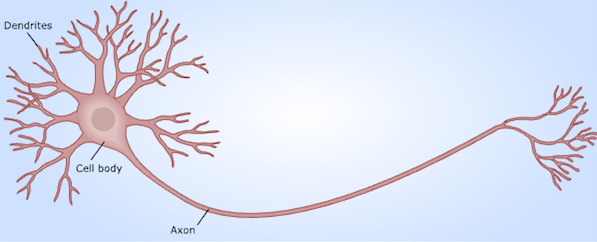
The function of a neuron can be modeled mathematically. Each
neuron, modeled as a node in the neural network, receives
input signal or stimulus from 
 is the offset or bias,
is the offset or bias,  is the input signal from
the jth node,
is the input signal from
the jth node,  is the synaptic connectivity to the jth input
node:
is the synaptic connectivity to the jth input
node:
 |
(2) |
 and
and  , so that both the weight and pattern vectors are
augmented to become
, so that both the weight and pattern vectors are
augmented to become
![${\bf x}=[x_0=1,\,x_1,\cdots,x_d]^T$](img12.svg) and
and
![${\bf w}=[w_0=b,\,,w_1,\cdots,w_d]^T$](img13.svg) , and Eq. (1)
above can now be conveniently written as
, and Eq. (1)
above can now be conveniently written as
 |
(3) |
 |
(4) |
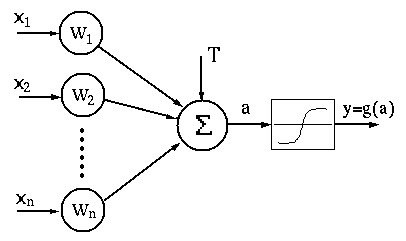
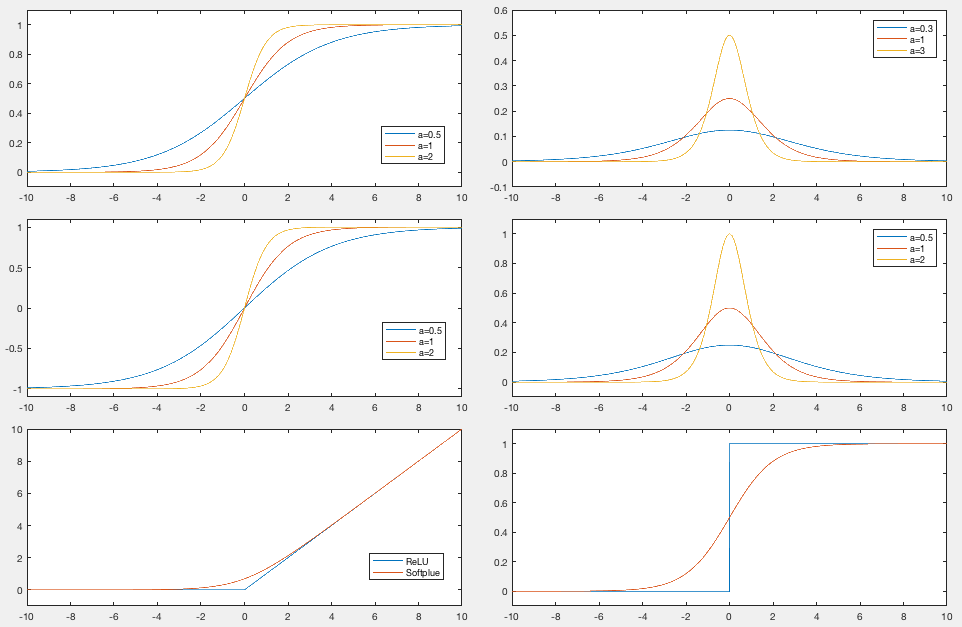
Here 
 |
(5) |
 |
(6) |
 is a parameter that controls the slop of
is a parameter that controls the slop of  . Specially,
when
. Specially,
when
 ,
,  becomes linear, but whn
becomes linear, but whn
 ,
,  becomes a threshold function:
becomes a threshold function:
 |
(7) |
 |
(8) |
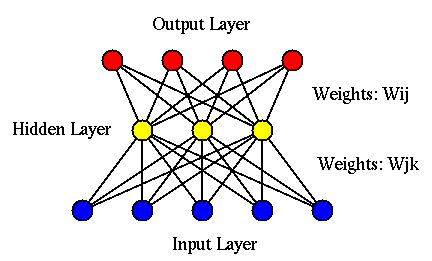
The function of a neural network can be modeled mathematically as a hierarchical structure shown below containing multiple layers of neurons, called nodes in the context of artificial neural networks:
The learning paradigms of the neural networks are listed below, depending on the interpretations of the input and output of the neural network.
This is the most general form of neural networks that learns and stores the associative relationship between two sets of patterns represented by vectors.
 pairs of patterns
pairs of patterns
 is presented to the
network which then learns to establish the associative relationship
between two sets of patterns:
is presented to the
network which then learns to establish the associative relationship
between two sets of patterns:
 |
(9) |
 in a pair is presented
as the input, the network produces an output pattern
in a pair is presented
as the input, the network produces an output pattern  associated to the output.
associated to the output.
Human memory is associative in the sense that given one pattern,
some associated pattern(s) may be produced. Examples include:
(Evolution, Darwin), (Einstein, 
As a special pattern associator, auto-associator associates a prestored pattern to an incomplete or noisy version of the pattern.
 is presented to the network for it to learn and remember, i.e.,
the patterns are stored in the network.
is presented to the network for it to learn and remember, i.e.,
the patterns are stored in the network.
This is another special kind of pattern associator which takes
a vector input



 , the network is model
the function.
, the network is model
the function.
 , the output value
produced by the single output node is an estimated function
value
, the output value
produced by the single output node is an estimated function
value
 .
.
This is a variation of the pattern associator of which the output
patterns are a set of categorical symbols representing different
classes

 |
(10) |
This is an unsupervised learning process. The network discovers automatically the regularity in the inputs so that similar patterns are automatically detected and grouped together in the same cluster or class.