When solving a linear equation system
 with
with  equations
and
equations
and  unknowns, the coefficient matrix
unknowns, the coefficient matrix  has
has  rows and
rows and  columns (
columns ( ). We need to answer some questions:
). We need to answer some questions:
- If the system has fewer equations than unknowns (
 ), are there
infinite solutions?
), are there
infinite solutions?
- If the system has more equations than unknowns (
 ), is there
no solution?
), is there
no solution?
- Does the solution exist, i.e., can we find a solution
 so
that
so
that
 holds?
holds?
- If a solution exists, is it unique? If it is not unique, how can
we find all solutions?
- If no solution exists, can we still find the optimal approximate
solution
 so that the error
so that the error
 is minimized?
is minimized?
The fundamental theorem of linear algebra can reveal the structure
of the solutions of any given linear system
 , and thereby
answer all questions above.
, and thereby
answer all questions above.
The  coefficient matrix
coefficient matrix
 can be
expressed in terms of either its
can be
expressed in terms of either its  M-D column vectors
M-D column vectors  or its
or its
 N-D row vectors
N-D row vectors
 :
:
![$\displaystyle {\bf A}=\left[\begin{array}{ccc}a_{11}&\cdots&a_{1N}\\
\vdots&\d...
...N]
=\left[\begin{array}{c}{\bf r}^T_1\\ \vdots\\ {\bf r}^T_M\end{array}\right],$](img386.svg) |
(134) |
![$\displaystyle {\bf A}^T=\left[\begin{array}{ccc}a_{11}&\cdots&a_{M1}\\
\vdots&...
..._M]
=\left[\begin{array}{c}{\bf c}^T_1\\ \vdots\\ {\bf c}^T_N\end{array}\right]$](img387.svg) |
(135) |
where
 and
and
 are respectively the ith row vector and jth column vector (all vectors
are assumed to be vertical):
are respectively the ith row vector and jth column vector (all vectors
are assumed to be vertical):
![$\displaystyle {\bf c}_j=\left[\begin{array}{c}a_{1j}\\ \vdots\\ a_{Mj}\end{arra...
...}_i=\left[\begin{array}{c}a_{i1}\\ \vdots\\ a_{iN}\end{array}\right]
\;\;\;\;\;$](img390.svg) i.e. i.e.![$\displaystyle \;\;\; {\bf r}_i^T=[a_{i1},\cdots,a_{iN}]$](img391.svg) |
(136) |
In general a function  can be represented by
can be represented by
 , where
, where
 is the
domain
of the function, the set of all input or argument values;
is the
domain
of the function, the set of all input or argument values;
 the codomain
of the function, the set into which all outputs of the function
are constrained to fall;
the codomain
of the function, the set into which all outputs of the function
are constrained to fall;
- the set of
 for all
for all  is the
image
of the function, a subset of the codomain.
is the
image
of the function, a subset of the codomain.
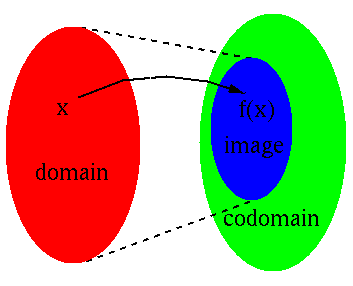
The matrix  can be considered as a function, a linear
transformation
can be considered as a function, a linear
transformation
 , which maps an N-D
vector
, which maps an N-D
vector
 in the domain of the function
into an M-D vector
in the domain of the function
into an M-D vector
 in the codomain of the function.
The fundamental theorem of linear algebra
concerns the following four subspaces associated with any
in the codomain of the function.
The fundamental theorem of linear algebra
concerns the following four subspaces associated with any  matrix
matrix  with rank
with rank
 (i.e.,
(i.e.,
 has
has  independent columns and rows).
independent columns and rows).
- The column space (image)
of
 is a space spanned by its
is a space spanned by its  M-D column vectors
(of which
M-D column vectors
(of which  are independent):
are independent):
 |
(137) |
which is an R-D subspace of
 composed of all possible
linear combinations of its
composed of all possible
linear combinations of its  column vectors:
column vectors:
![$\displaystyle x_1{\bf c}_1+\cdots+x_N{\bf c}_N=[{\bf c_1},\cdots,{\bf c}_N]
\le...
...begin{array}{c}x_1\\ \vdots\\ x_N\end{array}\right]
={\bf A}{\bf x}\;\;\;\;\;\;$](img405.svg)  |
(138) |
The column space
 is the image of the linear
transformation
is the image of the linear
transformation
 , and the equation
, and the equation
 is solvable if and only if
is solvable if and only if
 .
The dimension of the column space is the rank of
.
The dimension of the column space is the rank of
 ,
,
 .
.
- The row space
of
 (the column space of
(the column space of  ) is a space spanned by
its
) is a space spanned by
its  N-D row vectors (of which
N-D row vectors (of which  are independent):
are independent):
 |
(139) |
which is an R-D subspace of
 composed of all possible
linear combinations of its
composed of all possible
linear combinations of its  row vectors:
row vectors:
![$\displaystyle y_1{\bf r}_1+\cdots+y_M{\bf r}_N=[{\bf r_1},\cdots,{\bf r}_M]
\le...
...gin{array}{c}y_1\\ \vdots\\ y_M\end{array}\right]
={\bf A}^T{\bf y}\;\;\;\;\;\;$](img414.svg)  |
(140) |
The row space
 is the image of the linear
transformation
is the image of the linear
transformation
 , and the
equation
, and the
equation
 is solvable if and only if
is solvable if and only if
 .
As the rows and columns in
.
As the rows and columns in  are respectively the columns
and rows in
are respectively the columns
and rows in  , the row space of
, the row space of  is the column
space of
is the column
space of  , and the column space of
, and the column space of  is the row
space of
is the row
space of  :
:
 |
(141) |
The rank
 is the number of linearly independent
rows and columns of
is the number of linearly independent
rows and columns of  , i.e., the row space and the column
space have the same dimension, both equal to the rank of
, i.e., the row space and the column
space have the same dimension, both equal to the rank of  :
:
 |
(142) |
- The null space (kernel)
of
 , denoted by
, denoted by
 , is the set of all N-D
vectors
, is the set of all N-D
vectors  that satisfy the homogeneous equation
that satisfy the homogeneous equation
![$\displaystyle {\bf A}{\bf x}=\left[\begin{array}{c}{\bf r}^T_1\\ \vdots\\ {\bf r}^T_M\end{array}\right]
{\bf x}={\bf0},\;\;\;\;\;\;$](img424.svg) or or |
(143) |
i.e.,
 |
(144) |
In particular, when
 , we get
, we get
 ,
i.e., the origin
,
i.e., the origin
 is in the null space.
is in the null space.
As
 for any
for any
 and
and
 , we see that the null space
, we see that the null space
 and the row space
and the row space
 are orthogonal to each
other,
are orthogonal to each
other,
 .
.
The dimension of the null space is called the nullity of
 :
:
 . The
rank-nullity theorem
states the sum of the rank and the nullity of an
. The
rank-nullity theorem
states the sum of the rank and the nullity of an  matrix
matrix
 is equal to
is equal to  :
:
rank |
(145) |
We therefore see that
 and
and
 are two mutually
exclusive and complementary subspaces of
are two mutually
exclusive and complementary subspaces of
 :
:
 |
(146) |
i.e., they are
orthogonal complement
of each other, denoted by
 |
(147) |
Any N-D vector
 is in either of the two
subspaces
is in either of the two
subspaces
 and
and
 .
.
- The null space of
 (left null space of
(left null space of  ,
denoted by
,
denoted by
 , is the set of all M-D vectors
, is the set of all M-D vectors  that satisfy the homogeneous equation
that satisfy the homogeneous equation
![$\displaystyle {\bf A}^T{\bf y}=[{\bf c}_1,\cdots,{\bf c}_N]^T{\bf y}
=\left[\be...
...\bf c}^T_1\\ \vdots\\ {\bf c}^T_N\end{array}\right]
{\bf y}={\bf0},\;\;\;\;\;\;$](img441.svg) or or |
(148) |
i.e.,
 |
(149) |
As all
 are orthogonal to
are orthogonal to
 ,
,
 is orthogonal to the column space
is orthogonal to the column space
 :
:
 |
(150) |
We see that
 and
and
 are two mutually exclusive and
complementary subspaces of
are two mutually exclusive and
complementary subspaces of
 :
:
| |
|
 |
|
| |
i.e. |
 |
(151) |
Any M-D vector
 is in either of the two subspaces
is in either of the two subspaces
 and
and
 .
.
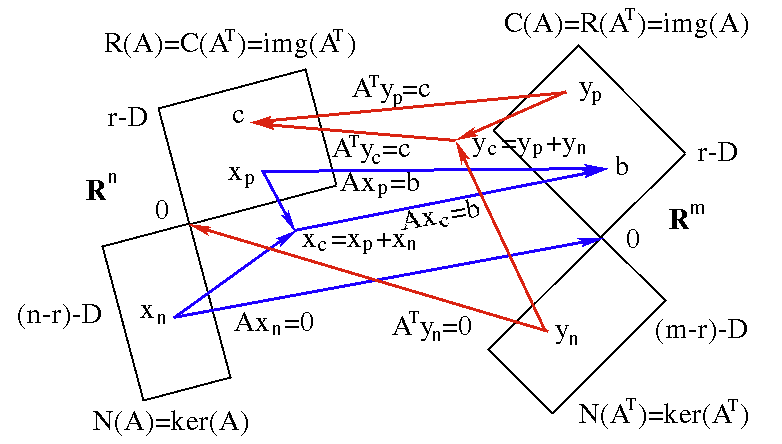
The four subspaces are summarized in the figure below, showing the domain
 (left) and the codomain
(left) and the codomain
 (right) of the linear mapping
(right) of the linear mapping
 , where
, where
-
 is the particular solution that is
mapped to
is the particular solution that is
mapped to
 , the image of
, the image of
 ;
;
-
 is a homogeneous solution that is
mapped to
is a homogeneous solution that is
mapped to
 ;
;
-
 is the complete solution that is
mapped to
is the complete solution that is
mapped to
 .
.
On the other hand,
 ,
,
 , and
, and
 are
respectively the particular, homogeneous and complete solutions of
are
respectively the particular, homogeneous and complete solutions of
 .
Here we have assumed
.
Here we have assumed
 and
and
 , i.e., both
, i.e., both
 and
and
 are solvable. We will also consider
the case where
are solvable. We will also consider
the case where
 later.
later.
Based on the rank
 of any
of any  matrix
matrix  ,
we can determine the dimensionalities of the four associated spaces and
the existence and uniqueness of solution of the system
,
we can determine the dimensionalities of the four associated spaces and
the existence and uniqueness of solution of the system
 :
:
- If
 ,
,
 ,
then
,
then
 , unique solution exists;
, unique solution exists;
- If
 ,
,
 ,
,
 ,
then
,
then
 , infinite solutions exist;
, infinite solutions exist;
- If
 ,
,
 ,
,
 ,
then unique solution exists if
,
then unique solution exists if
 ,
but no solution otherwise;
,
but no solution otherwise;
- If
 ,
,
 ,
,
 ,
then infinite solutions exist if
,
then infinite solutions exist if
 ,
but no solution otherwise.
,
but no solution otherwise.
We now consider specifically how to find the solutions of the system
 in light of the four subspaces of
in light of the four subspaces of  defined
above, through the examples below.
defined
above, through the examples below.
Example 1:
Solve the homogeneous equation system:
![$\displaystyle {\bf A}{\bf x}=\left[\begin{array}{ccc}1&2&5\\ 2&3&8\\ 3&1&5\end{...
..._3\end{array}\right]
=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]
={\bf0}$](img475.svg) |
(152) |
We first convert  into the rref:
The
into the rref:
The
 columns in the rref containing a single 1,
called a pivot, are called the pivot columns, and the
rows containing a pivot are called the pivot rows. Here,
columns in the rref containing a single 1,
called a pivot, are called the pivot columns, and the
rows containing a pivot are called the pivot rows. Here,
 , i.e.,
, i.e.,  is a singular matrix. The two pivot
rows
is a singular matrix. The two pivot
rows
![${\bf r}_1^T=[1,\;0,\;1]$](img479.svg) and
and
![${\bf r}_2^T=[0,\;1,\;2]$](img480.svg) can
be used as the basis vectors that span the row space
can
be used as the basis vectors that span the row space
 :
Note that the pivot columns of the rref do not span the column space
:
Note that the pivot columns of the rref do not span the column space
 , as the row reduction operations do not preserve the
columns of
, as the row reduction operations do not preserve the
columns of  . But they indicate the corresponding columns
. But they indicate the corresponding columns
![${\bf c}_1=[1\;2\;3]^T$](img482.svg) and
and
![${\bf c}_2=[2\;3\;1]^T$](img483.svg) in the original
matrix
in the original
matrix  can be used as the basis that spans
can be used as the basis that spans
 .
In general the bases of the row and column spaces so obtained are
not orthogonal.
.
In general the bases of the row and column spaces so obtained are
not orthogonal.
The  pivot rows are the independent equations in the system of
pivot rows are the independent equations in the system of  equations, and the variables corresponding to the pivot columns
(here
equations, and the variables corresponding to the pivot columns
(here  and
and  ) are the pivot variables. The remaining
) are the pivot variables. The remaining
 non-pivot rows containing all zeros are not independent, and the
variables corresponding to the non-pivot rows are free variables
(here
non-pivot rows containing all zeros are not independent, and the
variables corresponding to the non-pivot rows are free variables
(here  ), which can take any values.
), which can take any values.
From the rref form of the equation, we get
If we let the free variable  , then we can get the two pivot
variables
, then we can get the two pivot
variables  and
and  , and a special homogeneous solution
, and a special homogeneous solution
![${\bf x}_h=[-1\;-2\;1]^T$](img492.svg) as a basis vector that spans the 1-D null
space
as a basis vector that spans the 1-D null
space
 . However, as the free variable
. However, as the free variable  can take any
value
can take any
value  , the complete solution is the entire 1-D null space:
, the complete solution is the entire 1-D null space:
Example 2:
Solve the non-homogeneous equation with the same coefficient
matrix  used in the previous example:
used in the previous example:
We use Gauss-Jordan elimination to solve this system:
The  pivot rows correspond to the independent equations in the
system, i.e.,
pivot rows correspond to the independent equations in the
system, i.e.,
 , while the remaining
, while the remaining  non-pivot
row does not play any role as they map any
non-pivot
row does not play any role as they map any  to
to  . As
. As
 is singular,
is singular,
 does not exist. However, we can
find the solution based on the rref of the system, which can also be
expressed in block matrix form:
does not exist. However, we can
find the solution based on the rref of the system, which can also be
expressed in block matrix form:
![$\displaystyle \left[\begin{array}{rrr}1&0&1\\ 0&1&2\\ 0&0&0\end{array}\right]
\...
...ray}\right]=
\left[\begin{array}{c}5\\ 7\\ 0\end{array}\right]
\;\;\;\;\;\;\;\;$](img501.svg) or or![$\displaystyle \;\;\;\;\;\;\;\;
\left[\begin{array}{rr}{\bf I}&{\bf F}\\ {\bf0}&...
...}\end{array}\right]
=\left[\begin{array}{c}{\bf b}_1\\ {\bf0}\end{array}\right]$](img502.svg) |
|
where
Solving the matrix equation above for
 , we get
If we let
, we get
If we let
 , we get a particular solution
, we get a particular solution
![${\bf x}_p=[5\;7\;0]^T$](img507.svg) , which can be expressed as a linear
combination of
, which can be expressed as a linear
combination of  and
and  that span
that span
 ,
and
,
and  that span
that span
 :
We see that this solution is not entirely in the row space
:
We see that this solution is not entirely in the row space
 .
In general, this is the case for all particular solutions so obtained.
.
In general, this is the case for all particular solutions so obtained.
Having found both the particular solution  and the
homogeneous solution
and the
homogeneous solution  , we can further find the complete
solution
, we can further find the complete
solution  as the sum of
as the sum of  and the entire
null space spanned by
and the entire
null space spanned by  :
:
Based on different constant  , we get a set of equally valid
solutions. For example, if
, we get a set of equally valid
solutions. For example, if  , then we get
These solutions have the same projection onto the row space
, then we get
These solutions have the same projection onto the row space
 , i.e., they have the same projections onto the two
basis vectors
, i.e., they have the same projections onto the two
basis vectors  and
and  that span
that span
 :
:
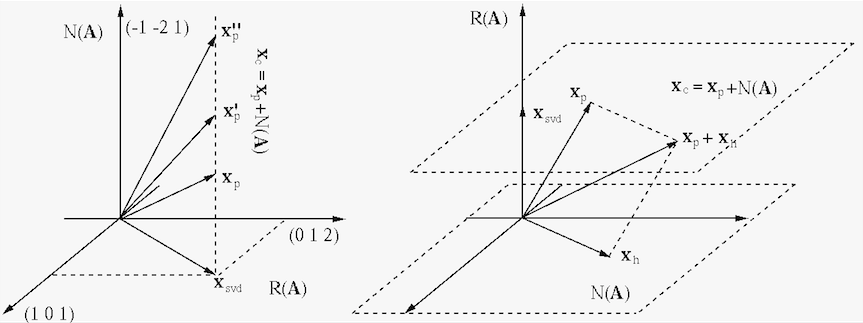
The figure below shows how the complete solution  can
be obtained as the sum of a particular solution
can
be obtained as the sum of a particular solution  in
in
 and the entire null space
and the entire null space
 . Here
. Here  and space
and space
 is composed of
is composed of
 and
and
 ,
respectively 2-D and 1-D on the left, but 1-D and 2-D on the right.
In either case, the complete solution is any particular solution
plus the entire null space, the vertical dashed line on the left,
the top dashed plane on the right. All points on the vertical line
or top satisfy the equation system, as they are have the same
projection onto the row space
,
respectively 2-D and 1-D on the left, but 1-D and 2-D on the right.
In either case, the complete solution is any particular solution
plus the entire null space, the vertical dashed line on the left,
the top dashed plane on the right. All points on the vertical line
or top satisfy the equation system, as they are have the same
projection onto the row space
 .
.
If the right hand side is
![${\bf b}'=[19,\,31,\,20]^T$](img518.svg) , then the
rref of the equation becomes:
, then the
rref of the equation becomes:
The non-pivot row is an impossible equation  , indicating that
no solution exists, as
, indicating that
no solution exists, as
 is not in the
column space spanned by
is not in the
column space spanned by
![${\bf r}_1=[1\;0\;1]^T$](img522.svg) and
and
![${\bf r}_2=[0\;1\;2]^T$](img523.svg) .
.
Example 3:
Find the complete solution of the following linear equation system:
This equation can be solved in the following steps:
If the right-hand side is
![${\bf b}'=[1,\;3,\;5]^T$](img550.svg) , then the row reduction
of the augmented matrix yields:
, then the row reduction
of the augmented matrix yields:
The equation corresponding to the last non-pivot row is  , indicating
the system is not solvable (even though the coefficient matrix does not
have full rank), because
, indicating
the system is not solvable (even though the coefficient matrix does not
have full rank), because
 is not in the column
space.
is not in the column
space.
Example 4: Consider the linear equation system with a
coefficient matrix  , the transpose of
, the transpose of  used in the
previous example:
used in the
previous example:
If the right-hand side is
![${\bf c}'=[1,\;1,\;2,\;3]^T$](img575.svg) ,
,
indicating the system is not solvable, as this
 , i.e., it is not in the column
space of
, i.e., it is not in the column
space of  or row space of
or row space of  .
.
In the two examples above, we have obtained all four subspaces associated
with this matrix  with
with  ,
,  , and
, and  , in terms of the
bases that span the subspaces:
, in terms of the
bases that span the subspaces:
- The row space
 is an R-D subspace of
is an R-D subspace of
 , spanned by the
, spanned by the  pivot rows of the rref of
pivot rows of the rref of
 :
:
- The null space
 is an (N-R)-D subspace of
is an (N-R)-D subspace of
 spanned by the
spanned by the  independent homogeneous solutions:
Note that the basis vectors of
independent homogeneous solutions:
Note that the basis vectors of
 are indeed orthogonal to those
of
are indeed orthogonal to those
of
 .
.
- The column space of
 is the same as the row space of
is the same as the row space of  ,
which is the R-D subspace of
,
which is the R-D subspace of  spanned by the two pivot rows of the
rref of
spanned by the two pivot rows of the
rref of  .
.
- The left null space
 is a (M-R)-D subspace of
is a (M-R)-D subspace of
 spanned by the homogeneous solutions (here one
spanned by the homogeneous solutions (here one  solution):
Again note that the basis vectors of
solution):
Again note that the basis vectors of
 are orthogonal to those
of
are orthogonal to those
of
 .
.
In general, here are the ways to find the bases of the four subspaces:
- The basis vectors of
 are the pivot rows of the rref
of
are the pivot rows of the rref
of  .
.
- The basis vectors of
 are the pivot rows of the rref
of
are the pivot rows of the rref
of  .
.
- The basis vectors of
 are the independent homogeneous
solutions of
are the independent homogeneous
solutions of
 . To find them, reduce
. To find them, reduce  to the
rref, identify all free variables
to the
rref, identify all free variables  corresponding to non-pivot
columns, set one of them to 1 and the rest to 0, solve homogeneous
system
corresponding to non-pivot
columns, set one of them to 1 and the rest to 0, solve homogeneous
system
 to find the pivot variables
to find the pivot variables  to get one basis vector. Repeat the process for each of the free
variables to get all basis vectors.
to get one basis vector. Repeat the process for each of the free
variables to get all basis vectors.
- The basis vectors of
 can be obtained by doing the
same as above for
can be obtained by doing the
same as above for  .
.
Note that while the basis of
 are the pivot rows of the
rref of
are the pivot rows of the
rref of  , as its rows are equivalent to those of
, as its rows are equivalent to those of  ,
the pivot columns of the rref basis of
,
the pivot columns of the rref basis of
 are not the basis
of
are not the basis
of
 , as the columns of
, as the columns of  have been changed by the
row deduction operations and are therefore not equivalent to the
columns of the resulting rref. The columns in
have been changed by the
row deduction operations and are therefore not equivalent to the
columns of the resulting rref. The columns in  corresponding
to the pivot columns in the rref could be used as the basis of
corresponding
to the pivot columns in the rref could be used as the basis of
 .
Alternatively, the basis of
.
Alternatively, the basis of
 can be obtained from the rref
of
can be obtained from the rref
of  , as its rows are equivalent to those of
, as its rows are equivalent to those of  , which
are the columns of
, which
are the columns of  .
.
We further make the following observations:
- The basis vectors of each of the four subspaces are independent,
the basis vectors of
 and
and
 are orthogonal,
and
are orthogonal,
and
 . Similarly, the basis vectors
of
. Similarly, the basis vectors
of
 and
and
 are orthogonal, and
are orthogonal, and
 .
In other words, the four subspaces indeed satisfy the following orthogonal
and complementary properties:
.
In other words, the four subspaces indeed satisfy the following orthogonal
and complementary properties:
 |
(155) |
i.e., they are orthogonal complements:
 .
.
- For
 to be solvable, the constant vector
to be solvable, the constant vector
 on the right-hand side must be in the column space,
on the right-hand side must be in the column space,
 . Otherwise the equation is not solvable,
even if
. Otherwise the equation is not solvable,
even if  . Similarly, for
. Similarly, for
 to be
solvable,
to be
solvable,  must be in the row space
must be in the row space
 .
In the examples above, both
.
In the examples above, both  and
and  are indeed in
their corresponding column spaces:
are indeed in
their corresponding column spaces:
![$\displaystyle {\bf b}=\left[\begin{array}{r}3\\ 2\\ 4\end{array}\right]
=3\left...
...}\right]
+11\left[\begin{array}{r}0\\ 1\\ 2\\ 3\end{array}\right]\in R({\bf A})$](img598.svg) |
(156) |
But as
![${\bf b}=[1,\;3,\;5]^T\notin C({\bf A})$](img599.svg) and
and
![${\bf c}=[1,\;1,\;2,\;3]^T\notin R({\bf A})$](img600.svg) , the corresponding
systems have no solutions.
, the corresponding
systems have no solutions.
- All homogeneous solutions of
 are in
the null space
are in
the null space
 , but in general the
particular solutions
, but in general the
particular solutions
 are not necessarily in the row space
are not necessarily in the row space
 . In the example
above,
. In the example
above,
 is a linear combination of the
is a linear combination of the  basis vectors of
basis vectors of
 and
and  basis vectors of
basis vectors of
 :
:
![$\displaystyle {\bf x}_p=\left[\begin{array}{r}-1\\ 2\\ 0\\ 0\end{array}\right]
...
...\begin{array}{r}2\\ -3\\ 0\\ 1\end{array}\right]\right)
={\bf x}'_p+{\bf x}''_p$](img604.svg) |
(157) |
where
![$\displaystyle {\bf x}'_p=\left[\begin{array}{c}0.1\\ 0.2\\ 0.3\\ 0.4\end{array}...
...\left[\begin{array}{c}-1.1\\ 1.8\\ -0.3\\ -0.4\end{array}\right]
\in N({\bf A})$](img605.svg) |
(158) |
are the projections of  onto
onto
 and
and
 ,
respectively, and
,
respectively, and
 is another particular solution without
any homogeneous component that satisfies
is another particular solution without
any homogeneous component that satisfies
 , while
, while
 is a homogeneous solution satisfying
is a homogeneous solution satisfying
 .
.
- All homogeneous solutions of
 are in
the left null space
are in
the left null space
 , but in general the
particular solutions
, but in general the
particular solutions
 are not necessarily in the column space. In the example above,
are not necessarily in the column space. In the example above,
 is a linear combination of the
is a linear combination of the  basis vectors
of
basis vectors
of
 and
and  basis vector of
basis vector of
 :
:
![$\displaystyle {\bf y}_p=\left[\begin{array}{r}7\\ -1\\ 0\end{array}\right]
=\le...
...
-2.5\left[\begin{array}{r}-2\\ 1\\ 1\end{array}\right]
={\bf y}'_p+{\bf y}''_p$](img610.svg) |
(159) |
where
![${\bf y}'_p=[2,\;1.5,\;2.5]^T\in C({\bf A})$](img611.svg) is a particular
solution (without any homogeneous component) that satisfies
is a particular
solution (without any homogeneous component) that satisfies
 .
.
Here is a summary of the four subspaces associated with an  by
by  matrix
matrix
 of rank
of rank  .
.
 , ,  , ,  |
dim
 |
dim
 |
dim
 |
dim
 |
solvability of
 |
 |
 |
0 |
 |
0 |
solvable,
 is unique solution
is unique solution |
 |
 |
0 |
 |
 |
over-constrained, solvable if
 |
 |
 |
 |
 |
0 |
under-constrained, solvable,
infinite solutions
 |
 |
 |
 |
 |
 |
solvable only if
 , infinite solutions , infinite solutions |
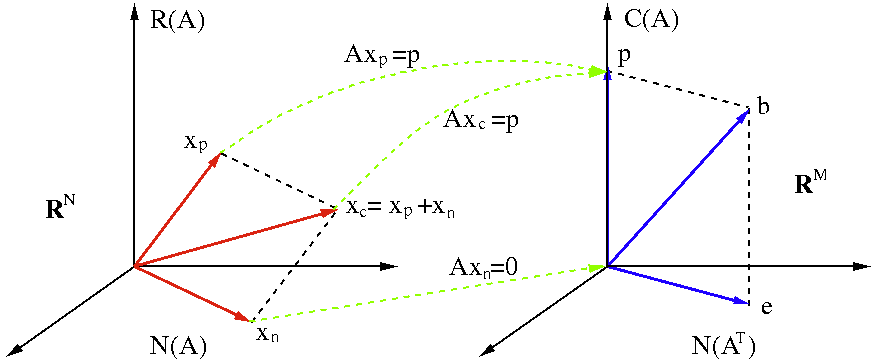
The figure below illustrates a specific case with  and
and  .
As
.
As
 , the system can only be approximately
solved to find
, the system can only be approximately
solved to find
 , which is the projection
of
, which is the projection
of  onto the column space
onto the column space
 . The error
. The error
 is minimized,
is minimized,
 is the optimal approximation. We will consider ways to obtain
this optimal approximation in the following sections.
is the optimal approximation. We will consider ways to obtain
this optimal approximation in the following sections.







 ), are there
infinite solutions?
), are there
infinite solutions?
 ), is there
no solution?
), is there
no solution?
 so
that
so
that
 holds?
holds?
 so that the error
so that the error
 is minimized?
is minimized?
 , and thereby
answer all questions above.
, and thereby
answer all questions above.






![$\displaystyle {\bf A}=\left[\begin{array}{ccc}a_{11}&\cdots&a_{1N}\\
\vdots&\d...
...N]
=\left[\begin{array}{c}{\bf r}^T_1\\ \vdots\\ {\bf r}^T_M\end{array}\right],$](img386.svg)
![$\displaystyle {\bf A}^T=\left[\begin{array}{ccc}a_{11}&\cdots&a_{M1}\\
\vdots&...
..._M]
=\left[\begin{array}{c}{\bf c}^T_1\\ \vdots\\ {\bf c}^T_N\end{array}\right]$](img387.svg)
 and
and
 are respectively the ith row vector and jth column vector (all vectors
are assumed to be vertical):
are respectively the ith row vector and jth column vector (all vectors
are assumed to be vertical):
![$\displaystyle {\bf c}_j=\left[\begin{array}{c}a_{1j}\\ \vdots\\ a_{Mj}\end{arra...
...}_i=\left[\begin{array}{c}a_{i1}\\ \vdots\\ a_{iN}\end{array}\right]
\;\;\;\;\;$](img390.svg) i.e.
i.e.![$\displaystyle \;\;\; {\bf r}_i^T=[a_{i1},\cdots,a_{iN}]$](img391.svg)


 is the
domain
of the function, the set of all input or argument values;
is the
domain
of the function, the set of all input or argument values;
 the codomain
of the function, the set into which all outputs of the function
are constrained to fall;
the codomain
of the function, the set into which all outputs of the function
are constrained to fall;
 for all
for all  is the
image
of the function, a subset of the codomain.
is the
image
of the function, a subset of the codomain.










 is a space spanned by its
is a space spanned by its  M-D column vectors
(of which
M-D column vectors
(of which  are independent):
are independent):

 composed of all possible
linear combinations of its
composed of all possible
linear combinations of its  column vectors:
column vectors:
![$\displaystyle x_1{\bf c}_1+\cdots+x_N{\bf c}_N=[{\bf c_1},\cdots,{\bf c}_N]
\le...
...begin{array}{c}x_1\\ \vdots\\ x_N\end{array}\right]
={\bf A}{\bf x}\;\;\;\;\;\;$](img405.svg)

 is the image of the linear
transformation
is the image of the linear
transformation
 , and the equation
, and the equation
 is solvable if and only if
is solvable if and only if
 .
The dimension of the column space is the rank of
.
The dimension of the column space is the rank of
 ,
,
 .
.
 (the column space of
(the column space of  ) is a space spanned by
its
) is a space spanned by
its  N-D row vectors (of which
N-D row vectors (of which  are independent):
are independent):

 composed of all possible
linear combinations of its
composed of all possible
linear combinations of its  row vectors:
row vectors:
![$\displaystyle y_1{\bf r}_1+\cdots+y_M{\bf r}_N=[{\bf r_1},\cdots,{\bf r}_M]
\le...
...gin{array}{c}y_1\\ \vdots\\ y_M\end{array}\right]
={\bf A}^T{\bf y}\;\;\;\;\;\;$](img414.svg)

 is the image of the linear
transformation
is the image of the linear
transformation
 , and the
equation
, and the
equation
 is solvable if and only if
is solvable if and only if
 .
As the rows and columns in
.
As the rows and columns in  are respectively the columns
and rows in
are respectively the columns
and rows in  , the row space of
, the row space of  is the column
space of
is the column
space of  , and the column space of
, and the column space of  is the row
space of
is the row
space of  :
:

 is the number of linearly independent
rows and columns of
is the number of linearly independent
rows and columns of  , i.e., the row space and the column
space have the same dimension, both equal to the rank of
, i.e., the row space and the column
space have the same dimension, both equal to the rank of  :
:

 , denoted by
, denoted by
 , is the set of all N-D
vectors
, is the set of all N-D
vectors  that satisfy the homogeneous equation
that satisfy the homogeneous equation
![$\displaystyle {\bf A}{\bf x}=\left[\begin{array}{c}{\bf r}^T_1\\ \vdots\\ {\bf r}^T_M\end{array}\right]
{\bf x}={\bf0},\;\;\;\;\;\;$](img424.svg) or
or

 , we get
, we get
 ,
i.e., the origin
,
i.e., the origin
 is in the null space.
is in the null space.












 and
and
 are two mutually
exclusive and complementary subspaces of
are two mutually
exclusive and complementary subspaces of
 :
:


 is in either of the two
subspaces
is in either of the two
subspaces
 and
and
 .
.
 (left null space of
(left null space of  ,
denoted by
,
denoted by
 , is the set of all M-D vectors
, is the set of all M-D vectors  that satisfy the homogeneous equation
that satisfy the homogeneous equation
![$\displaystyle {\bf A}^T{\bf y}=[{\bf c}_1,\cdots,{\bf c}_N]^T{\bf y}
=\left[\be...
...\bf c}^T_1\\ \vdots\\ {\bf c}^T_N\end{array}\right]
{\bf y}={\bf0},\;\;\;\;\;\;$](img441.svg) or
or

 are orthogonal to
are orthogonal to
 ,
,
 is orthogonal to the column space
is orthogonal to the column space
 :
:

 and
and
 are two mutually exclusive and
complementary subspaces of
are two mutually exclusive and
complementary subspaces of
 :
:


 is in either of the two subspaces
is in either of the two subspaces
 and
and
 .
.



 is the particular solution that is
mapped to
is the particular solution that is
mapped to
 , the image of
, the image of
 ;
;
 is a homogeneous solution that is
mapped to
is a homogeneous solution that is
mapped to
 ;
;
 is the complete solution that is
mapped to
is the complete solution that is
mapped to
 .
.
 ,
,
 , and
, and
 are
respectively the particular, homogeneous and complete solutions of
are
respectively the particular, homogeneous and complete solutions of
 .
Here we have assumed
.
Here we have assumed
 and
and
 , i.e., both
, i.e., both
 and
and
 are solvable. We will also consider
the case where
are solvable. We will also consider
the case where
 later.
later.





 ,
,
 ,
then
,
then
 , unique solution exists;
, unique solution exists;
 ,
,
 ,
,
 ,
then
,
then
 , infinite solutions exist;
, infinite solutions exist;
 ,
,
 ,
,
 ,
then unique solution exists if
,
then unique solution exists if
 ,
but no solution otherwise;
,
but no solution otherwise;
 ,
,
 ,
,
 ,
then infinite solutions exist if
,
then infinite solutions exist if
 ,
but no solution otherwise.
,
but no solution otherwise.


![$\displaystyle {\bf A}{\bf x}=\left[\begin{array}{ccc}1&2&5\\ 2&3&8\\ 3&1&5\end{...
..._3\end{array}\right]
=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]
={\bf0}$](img475.svg)
 into the rref:
into the rref:
![$\displaystyle \left[\begin{array}{ccc}1&2&5\\ 2&3&8\\ 3&1&5\end{array}\right]
\...
... x_2\\ x_3\end{array}\right]
=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$](img476.svg)
 columns in the rref containing a single 1,
called a pivot, are called the pivot columns, and the
rows containing a pivot are called the pivot rows. Here,
columns in the rref containing a single 1,
called a pivot, are called the pivot columns, and the
rows containing a pivot are called the pivot rows. Here,
 , i.e.,
, i.e.,  is a singular matrix. The two pivot
rows
is a singular matrix. The two pivot
rows
![${\bf r}_1^T=[1,\;0,\;1]$](img479.svg) and
and
![${\bf r}_2^T=[0,\;1,\;2]$](img480.svg) can
be used as the basis vectors that span the row space
can
be used as the basis vectors that span the row space
 :
:
![$\displaystyle R({\bf A})=c_1{\bf r}_1+c_2{\bf r}_2
=c_1\left[\begin{array}{r}1\\ 0\\ 1\end{array}\right]
+c_2\left[\begin{array}{r}0\\ 1\\ 2\end{array}\right]$](img481.svg)
 , as the row reduction operations do not preserve the
columns of
, as the row reduction operations do not preserve the
columns of  . But they indicate the corresponding columns
. But they indicate the corresponding columns
![${\bf c}_1=[1\;2\;3]^T$](img482.svg) and
and
![${\bf c}_2=[2\;3\;1]^T$](img483.svg) in the original
matrix
in the original
matrix  can be used as the basis that spans
can be used as the basis that spans
 .
In general the bases of the row and column spaces so obtained are
not orthogonal.
.
In general the bases of the row and column spaces so obtained are
not orthogonal.







 , then we can get the two pivot
variables
, then we can get the two pivot
variables  and
and  , and a special homogeneous solution
, and a special homogeneous solution
![${\bf x}_h=[-1\;-2\;1]^T$](img492.svg) as a basis vector that spans the 1-D null
space
as a basis vector that spans the 1-D null
space
 . However, as the free variable
. However, as the free variable  can take any
value
can take any
value  , the complete solution is the entire 1-D null space:
, the complete solution is the entire 1-D null space:
![$\displaystyle N({\bf A})=c {\bf x}_h=c\left[\begin{array}{r}-1\\ -2\\ 1\end{array}\right]$](img494.svg)

![$\displaystyle {\bf A}{\bf x}=
\left[\begin{array}{ccc}1&2&5\\ 2&3&8\\ 3&1&5\end...
...end{array}\right]
=\left[\begin{array}{c}19\\ 31\\ 22\end{array}\right]={\bf b}$](img495.svg)
![$\displaystyle [\begin{array}{cc}{\bf A}&{\bf b}\end{array}]
=\left[\begin{array...
...ow
\left[\begin{array}{rrr\vert r}1&0&1&5\\ 0&1&2&7\\ 0&0&0&0\end{array}\right]$](img496.svg)
 pivot rows correspond to the independent equations in the
system, i.e.,
pivot rows correspond to the independent equations in the
system, i.e.,
 , while the remaining
, while the remaining  non-pivot
row does not play any role as they map any
non-pivot
row does not play any role as they map any  to
to  . As
. As
 is singular,
is singular,
 does not exist. However, we can
find the solution based on the rref of the system, which can also be
expressed in block matrix form:
does not exist. However, we can
find the solution based on the rref of the system, which can also be
expressed in block matrix form:
![$\displaystyle \left[\begin{array}{rrr}1&0&1\\ 0&1&2\\ 0&0&0\end{array}\right]
\...
...ray}\right]=
\left[\begin{array}{c}5\\ 7\\ 0\end{array}\right]
\;\;\;\;\;\;\;\;$](img501.svg) or
or![$\displaystyle \;\;\;\;\;\;\;\;
\left[\begin{array}{rr}{\bf I}&{\bf F}\\ {\bf0}&...
...}\end{array}\right]
=\left[\begin{array}{c}{\bf b}_1\\ {\bf0}\end{array}\right]$](img502.svg)
![$\displaystyle {\bf I}=\left[\begin{array}{cc}1&0\\ 0&1\end{array}\right],\;\;\;...
...{free}=x_3,\;\;\;\;\;\;
{\bf b}_1=\left[\begin{array}{c}5\\ 7\end{array}\right]$](img503.svg)
 , we get
, we get
![$\displaystyle {\bf I}{\bf x}_{pivot}+{\bf F}{\bf x}_{free}={\bf b}_1,\;\;\;\;\;...
...{c}5\\ 7\end{array}\right]
+\left[\begin{array}{c}-1\\ -2\end{array}\right] x_3$](img505.svg)
 , we get a particular solution
, we get a particular solution
![${\bf x}_p=[5\;7\;0]^T$](img507.svg) , which can be expressed as a linear
combination of
, which can be expressed as a linear
combination of  and
and  that span
that span
 ,
and
,
and  that span
that span
 :
:
![$\displaystyle {\bf x}_p=\left[\begin{array}{c}5\\ 7\\ 0\end{array}\right]
=\fra...
...{array}\right]
-\frac{19}{6}\left[\begin{array}{r}-1\\ -2\\ 1\end{array}\right]$](img509.svg)
 .
In general, this is the case for all particular solutions so obtained.
.
In general, this is the case for all particular solutions so obtained.





![$\displaystyle {\bf x}_c=\left[\begin{array}{c}5\\ 7\\ 0\end{array}\right]
+c \l...
...ay}{r}-1\\ -2\\ 1\end{array}\right]
={\bf x}_p+c {\bf x}_h={\bf x}_p+N({\bf A})$](img512.svg)
 , we get a set of equally valid
solutions. For example, if
, we get a set of equally valid
solutions. For example, if  , then we get
, then we get
![$\displaystyle {\bf x}_0=\left[\begin{array}{c}5\\ 7\\ 0\end{array}\right],\;\;\...
...ay}\right],\;\;\;\;
{\bf x}_2=\left[\begin{array}{c}3\\ 3\\ 2\end{array}\right]$](img514.svg)
 , i.e., they have the same projections onto the two
basis vectors
, i.e., they have the same projections onto the two
basis vectors  and
and  that span
that span
 :
:











![${\bf b}'=[19,\,31,\,20]^T$](img518.svg)
![$\displaystyle \left[\begin{array}{rrr}1&0&1\\ 0&1&2\\ 0&0&0\end{array}\right]
\...
... x_2\\ x_3\end{array}\right]=
\left[\begin{array}{c}5\\ 7\\ 2\end{array}\right]$](img519.svg)
 , indicating that
no solution exists, as
, indicating that
no solution exists, as
 is not in the
column space spanned by
is not in the
column space spanned by
![${\bf r}_1=[1\;0\;1]^T$](img522.svg) and
and
![${\bf r}_2=[0\;1\;2]^T$](img523.svg) .
.
![$\displaystyle {\bf A}{\bf x}=\left[\begin{array}{rccc}1&2&3&4\\ 4&3&2&1\\ -2&1&...
...4\end{array}\right]
=\left[\begin{array}{r}3\\ 2\\ 4\end{array}\right] ={\bf b}$](img524.svg)
![$\displaystyle \left[\begin{array}{rrrr\vert r}1&2&3&4&3\\ 4&3&2&1&2\\ -2&1&4&7&4\end{array}\right]$](img525.svg)

![$\displaystyle \left[\begin{array}{rrrr\vert r}1&2&3&4&3\\ 0&-5&-10&-15&-10\\ 0&...
...t[\begin{array}{rrrr\vert r}1&2&3&4&3\\ 0&1&2&3&2\\ 0&0&0&0&0\end{array}\right]$](img527.svg)

![$\displaystyle \left[\begin{array}{rrrr\vert r}1&0&-1&-2&-1\\ 0&1&2&3&2\\ 0&0&0&...
...y}{rr\vert r}{\bf I}&{\bf F}&{\bf b_1}\\ {\bf0}&{\bf0}&{\bf0}\end{array}\right]$](img528.svg)
![${\bf r}_1^T=[1\;0\;-1\;-2]$](img529.svg) and
and
![${\bf r}_2^T=[0\;1\;2\;3]$](img530.svg) in the rref span
in the rref span
 , and the
two columns in the original matrix
, and the
two columns in the original matrix  corresponding to
the pivot columns in the rref,
corresponding to
the pivot columns in the rref,
![$[1\;4\;-2]^T$](img531.svg) and
and
![$[2\;3\;1]^T$](img532.svg) could
be used as the basis vectors that span
could
be used as the basis vectors that span
 .
.
![$\displaystyle \left[\begin{array}{rr}{\bf I}&{\bf F}\\ {\bf0}&{\bf0}\end{array}...
...f\end{array}\right]=
\left[\begin{array}{c}{\bf b_1}\\ {\bf0}\end{array}\right]$](img533.svg)
![$\displaystyle {\bf I}=\left[\begin{array}{cc}1&0\\ 0&1\end{array}\right],\;\;\;...
...ray}\right],\;\;\;\;\;
{\bf b}_1=\left[\begin{array}{r}-1\\ 2\end{array}\right]$](img534.svg)

 by setting
by setting
 :
:
 i.e.
i.e.![$\displaystyle \;\;\;\;\;
{\bf x}_p=\left[\begin{array}{c}x_1\\ x_2\end{array}\r...
...1&2\\ -2&-3\end{array}\right]
\left[\begin{array}{r}x_3\\ x_4\end{array}\right]$](img538.svg)
 be either of the two standard basis vectors
be either of the two standard basis vectors
![${\bf x}_f=[x_3,\;x_4]^T=[1\;0]^T$](img540.svg) and
and
![${\bf x}_f=[x_3,\;x_4]^T=[0\;1]^T$](img541.svg) of the null space
of the null space
 , and get
, and get
![$\displaystyle {\bf x}_p=\left[\begin{array}{c}x_1\\ x_2\end{array}\right]
=\left[\begin{array}{r}1\\ -2\end{array}\right]
\;\;\;\;\;$](img542.svg) or
or![$\displaystyle \;\;\;\;\;
\left[\begin{array}{r}2\\ -3\end{array}\right]$](img543.svg)
![$\displaystyle {\bf x}_{h1}=\left[\begin{array}{c}x_1\\ x_2\\ x_3\\ x_4\end{arra...
...\ x_4\end{array}\right]
=\left[\begin{array}{r}2\\ -3\\ 0\\ 1\end{array}\right]$](img544.svg)
 by setting
by setting

 i.e.
i.e.![$\displaystyle \;\;\;\;\;
\left[\begin{array}{c}x_1\\ x_2\end{array}\right]
=\left[\begin{array}{r}-1\\ 2\end{array}\right]
\;\;\;\;\;$](img547.svg) i.e.
i.e.![$\displaystyle \;\;\;\;\;\;\;
{\bf x}_p=\left[\begin{array}{r}-1\\ 2\\ 0\\ 0\end{array}\right]$](img548.svg)
![$\displaystyle {\bf x}_c={\bf x}_p+N({\bf A})
={\bf x}_p+c_1{\bf x}_{h1}+c_2{\bf...
... 0\end{array}\right]
+c_2\left[\begin{array}{r}2\\ -3\\ 0\\ 1\end{array}\right]$](img549.svg)
![${\bf b}'=[1,\;3,\;5]^T$](img550.svg)
![$\displaystyle \left[\begin{array}{rrrr\vert r}1&2&3&4&1\\ 4&3&2&1&3\\ -2&1&4&7&...
...egin{array}{rrrr\vert r}1&2&3&4&1\\ 0&1&2&3&0.2\\ 0&0&0&0&1.2\end{array}\right]$](img551.svg)
 , indicating
the system is not solvable (even though the coefficient matrix does not
have full rank), because
, indicating
the system is not solvable (even though the coefficient matrix does not
have full rank), because
 is not in the column
space.
is not in the column
space.


![$\displaystyle {\bf A}^T{\bf y}=\left[\begin{array}{rrr}1&4&-2\\ 2&3&1\\ 3&2&4\\...
...array}\right]
=\left[\begin{array}{c}3\\ 11\\ 19\\ 27\end{array}\right]={\bf c}$](img553.svg)
![$\displaystyle \left[\begin{array}{rrr\vert r}1&4&-2&3\\ 2&3&1&11\\ 3&2&4&19\\ 4...
...gin{array}{rrr\vert r}1&0&2&7\\ 0&1&-1&-1\\ 0&0&0&0\\ 0&0&0&0\end{array}\right]$](img554.svg)
![${\bf r}^T_1=[1\;0\;2]$](img555.svg) and
and
![${\bf r}^T_2=[0\;1\;-1]$](img556.svg) are the basis vectors that span
are the basis vectors that span
 . The two
vectors that span
. The two
vectors that span
 found in Example 3 can be expressed as
linear combinations of
found in Example 3 can be expressed as
linear combinations of  and
and  ,
,
![$[1\;4\;-2]^T={\bf r}_1+4{\bf r}_2$](img558.svg) and
and
![$[2\;3\;1]^T=2{\bf r}_1+3{\bf r}_2$](img559.svg) , i.e., either of the two pairs can
be used as the basis that span
, i.e., either of the two pairs can
be used as the basis that span
 .
.
![$\displaystyle \left[\begin{array}{cc}{\bf I}&{\bf F}\\ {\bf0}&{\bf0}\end{array}...
...f\end{array}\right]=
\left[\begin{array}{r}{\bf c}_1\\ {\bf0}\end{array}\right]$](img560.svg)
![$\displaystyle {\bf I}=\left[\begin{array}{cc}1&0\\ 0&1\end{array}\right],\;\;\;...
...bf y}_f=y_3,\;\;\;\;\;
{\bf c}_1=\left[\begin{array}{r}7\\ -1\end{array}\right]$](img561.svg)

 by setting
by setting
 and thereby
and thereby
 . We let
the free variable
. We let
the free variable
 and get
and get
 i.e.
i.e.![$\displaystyle \;\;\;\;\;
{\bf y}_p=-{\bf F}{\bf y}_f
=\left[\begin{array}{c}y_1...
...nd{array}\right]y_3
=\left[\begin{array}{r}-2\\ 1\end{array}\right],
\;\;\;\;\;$](img568.svg) i.e.
i.e.![$\displaystyle \;\;\;\;\;
{\bf y}_h=\left[\begin{array}{r}-2\\ 1\\ 1\end{array}\right]$](img569.svg)
 by setting
by setting
 :
:
![$\displaystyle {\bf I}{\bf y}_p+{\bf F}{\bf y}_f={\bf y}_p
={\bf c}_1=\left[\begin{array}{r}7\\ -1\end{array}\right],
\;\;\;\;\;$](img572.svg) i.e.
i.e.![$\displaystyle \;\;\;\;\;
{\bf y}_p=\left[\begin{array}{r}7\\ -1\\ 0\end{array}\right]$](img573.svg)
![$\displaystyle {\bf y}_c={\bf y}_p+N({\bf A}^T)={\bf y}_p+c y_3
=\left[\begin{ar...
...\ -1\\ 0\end{array}\right]+c
\left[\begin{array}{r}-2\\ 1\\ 1\end{array}\right]$](img574.svg)
![${\bf c}'=[1,\;1,\;2,\;3]^T$](img575.svg)
![$\displaystyle \left[\begin{array}{rrr\vert r}1&4&-2&1\\ 2&3&1&1\\ 3&2&4&2\\ 4&1...
...n{array}{rrr\vert r}1&4&-2&1\\ 0&1&-1&1/5\\ 0&0&0&1\\ 0&0&0&2\end{array}\right]$](img576.svg)
 , i.e., it is not in the column
space of
, i.e., it is not in the column
space of  or row space of
or row space of  .
.




 is an R-D subspace of
is an R-D subspace of
 , spanned by the
, spanned by the  pivot rows of the rref of
pivot rows of the rref of
 :
:
![$\displaystyle R({\bf A})=C({\bf A}^T)=
span\left(\left[\begin{array}{r}1\\ 0\\ ...
...end{array}\right],
\left[\begin{array}{c}0\\ 1\\ 2\\ 3\end{array}\right]\right)$](img581.svg)
 is an (N-R)-D subspace of
is an (N-R)-D subspace of
 spanned by the
spanned by the  independent homogeneous solutions:
independent homogeneous solutions:
![$\displaystyle N({\bf A})=span\left(\left[\begin{array}{r}1\\ -2\\ 1\\ 0\end{array}\right],
\left[\begin{array}{r}2\\ -3\\ 0\\ 1\end{array}\right] \right)$](img583.svg)
 are indeed orthogonal to those
of
are indeed orthogonal to those
of
 .
.
 is the same as the row space of
is the same as the row space of  ,
which is the R-D subspace of
,
which is the R-D subspace of  spanned by the two pivot rows of the
rref of
spanned by the two pivot rows of the
rref of  .
.
![$\displaystyle C({\bf A})=R({\bf A}^T)=span\left(\left[\begin{array}{c}1\\ 0\\ 2\end{array}\right],
\left[\begin{array}{r}0\\ 1\\ -1\end{array}\right]\right)$](img585.svg)
 is a (M-R)-D subspace of
is a (M-R)-D subspace of
 spanned by the homogeneous solutions (here one
spanned by the homogeneous solutions (here one  solution):
solution):
![$\displaystyle N({\bf A}^T)=span\left(\left[\begin{array}{r}-2\\ 1\\ 1\end{array}\right] \right)
=c\;\left[\begin{array}{r}-2\\ 1\\ 1\end{array}\right]$](img587.svg)
 are orthogonal to those
of
are orthogonal to those
of
 .
.
 are the pivot rows of the rref
of
are the pivot rows of the rref
of  .
.
 are the pivot rows of the rref
of
are the pivot rows of the rref
of  .
.
 are the independent homogeneous
solutions of
are the independent homogeneous
solutions of
 . To find them, reduce
. To find them, reduce  to the
rref, identify all free variables
to the
rref, identify all free variables  corresponding to non-pivot
columns, set one of them to 1 and the rest to 0, solve homogeneous
system
corresponding to non-pivot
columns, set one of them to 1 and the rest to 0, solve homogeneous
system
 to find the pivot variables
to find the pivot variables  to get one basis vector. Repeat the process for each of the free
variables to get all basis vectors.
to get one basis vector. Repeat the process for each of the free
variables to get all basis vectors.
 can be obtained by doing the
same as above for
can be obtained by doing the
same as above for  .
.












 and
and
 are orthogonal,
and
are orthogonal,
and
 . Similarly, the basis vectors
of
. Similarly, the basis vectors
of
 and
and
 are orthogonal, and
are orthogonal, and
 .
In other words, the four subspaces indeed satisfy the following orthogonal
and complementary properties:
.
In other words, the four subspaces indeed satisfy the following orthogonal
and complementary properties:

 .
.
 to be solvable, the constant vector
to be solvable, the constant vector
 on the right-hand side must be in the column space,
on the right-hand side must be in the column space,
 . Otherwise the equation is not solvable,
even if
. Otherwise the equation is not solvable,
even if  . Similarly, for
. Similarly, for
 to be
solvable,
to be
solvable,  must be in the row space
must be in the row space
 .
In the examples above, both
.
In the examples above, both  and
and  are indeed in
their corresponding column spaces:
are indeed in
their corresponding column spaces:
![$\displaystyle {\bf b}=\left[\begin{array}{r}3\\ 2\\ 4\end{array}\right]
=3\left...
...}\right]
+11\left[\begin{array}{r}0\\ 1\\ 2\\ 3\end{array}\right]\in R({\bf A})$](img598.svg)
![${\bf b}=[1,\;3,\;5]^T\notin C({\bf A})$](img599.svg) and
and
![${\bf c}=[1,\;1,\;2,\;3]^T\notin R({\bf A})$](img600.svg) , the corresponding
systems have no solutions.
, the corresponding
systems have no solutions.
 are in
the null space
are in
the null space
 , but in general the
particular solutions
, but in general the
particular solutions
 are not necessarily in the row space
are not necessarily in the row space
 . In the example
above,
. In the example
above,
 is a linear combination of the
is a linear combination of the  basis vectors of
basis vectors of
 and
and  basis vectors of
basis vectors of
 :
:
![$\displaystyle {\bf x}_p=\left[\begin{array}{r}-1\\ 2\\ 0\\ 0\end{array}\right]
...
...\begin{array}{r}2\\ -3\\ 0\\ 1\end{array}\right]\right)
={\bf x}'_p+{\bf x}''_p$](img604.svg)
![$\displaystyle {\bf x}'_p=\left[\begin{array}{c}0.1\\ 0.2\\ 0.3\\ 0.4\end{array}...
...\left[\begin{array}{c}-1.1\\ 1.8\\ -0.3\\ -0.4\end{array}\right]
\in N({\bf A})$](img605.svg)
 onto
onto
 and
and
 ,
respectively, and
,
respectively, and
 is another particular solution without
any homogeneous component that satisfies
is another particular solution without
any homogeneous component that satisfies
 , while
, while
 is a homogeneous solution satisfying
is a homogeneous solution satisfying
 .
.
 are in
the left null space
are in
the left null space
 , but in general the
particular solutions
, but in general the
particular solutions
 are not necessarily in the column space. In the example above,
are not necessarily in the column space. In the example above,
 is a linear combination of the
is a linear combination of the  basis vectors
of
basis vectors
of
 and
and  basis vector of
basis vector of
 :
:
![$\displaystyle {\bf y}_p=\left[\begin{array}{r}7\\ -1\\ 0\end{array}\right]
=\le...
...
-2.5\left[\begin{array}{r}-2\\ 1\\ 1\end{array}\right]
={\bf y}'_p+{\bf y}''_p$](img610.svg)
![${\bf y}'_p=[2,\;1.5,\;2.5]^T\in C({\bf A})$](img611.svg) is a particular
solution (without any homogeneous component) that satisfies
is a particular
solution (without any homogeneous component) that satisfies
 .
.




 ,
,  ,
, 








 is unique solution
is unique solution














 , infinite solutions
, infinite solutions







