Solving Over-Determined Linear Equation Systems

While solving a linear equation system ${\bf Ax}={\bf b}$, if $M>N$, i.e., there are more equations than unknowns, the equation system may be over-determined with no solution. In this case we can still find an approximated solution which is optimal in the least squares (LS) sense, i.e., the LS error defined below is minimized:

$$\varepsilon({\bf x}) = \frac{1}{2}\vert\vert{\bf r}\vert\vert^2 =\frac{1}{2}{\bf r}^T{\bf r} =\frac{1}{2} ({\bf b}-{\bf A}{\bf x})^T({\bf b}-{\bf A}{\bf x})$$

$$= \frac{1}{2}\left( {\bf b}^T{\bf b}-{\bf x}^T{\bf A}^T{\bf b}-{\bf b}^T{\bf A}{\bf x}+{\bf x}^T{\bf A}^T{\bf A}{\bf x}\right)$$ (122)

where ${\bf r}={\bf b}-{\bf A}{\bf x}$ is the residual of an approximated solution ${\bf x}$. To find this optimal solution, we set the derivative of the LS error to zero (see here):

$$\frac{d}{d{\bf x}}\varepsilon({\bf x})=\frac{1}{2}\frac{d}{d{\bf ... ...+{\bf x}^T{\bf A}^T{\bf A}{\bf x}\right) =-{\bf A}^T{\bf b}+{\bf A}^T{\bf Ax}=0$$ (123)

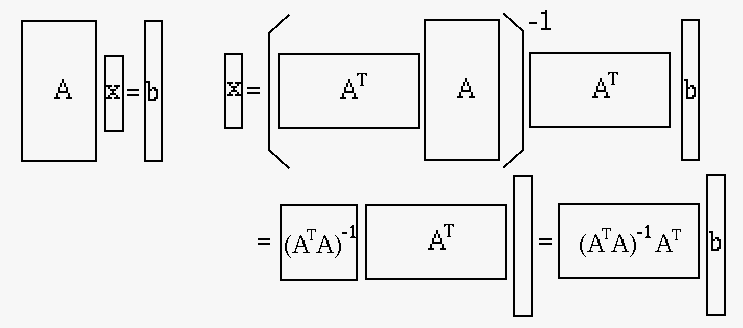
and solve this matrix equation to get

$${\bf x}=\left({\bf A}^T{\bf A}\right)^{-1}{\bf A}^T{\bf b}={\bf A}^-{\bf b}$$ (124)

where ${\bf A}^-=\left({\bf A}^T{\bf A}\right)^{-1}{\bf A}^T$ is the pseudo-inverse of the non-square matrix ${\bf A}$.

Here we assume the $N\times N$ matrix ${\bf A}^T{\bf A}$ has full rank with $R=N<M$ and therefore is invertible. However, if $R<N$, matrix ${\bf A}^T{\bf A}$ non-invertible. In this case, we can still find san approximated solution using the pseudo inverse of ${\bf A}$ based on its SVD:

$${\bf A}^-={\bf V}{\bf\Sigma}^-{\bf U}^T,\;\;\;\;\;\;\;\; {\bf x}={\bf A}^-{\bf b}={\bf V}{\bf\Sigma}^-{\bf U}^T{\bf b}$$ (125)

As we will show below, this solution is optimal in the LS sense.

Moreoever, even if matrix ${\bf A}$ is full rank with $R=N<M$, it may still be nearly singular, with a large condition number $\kappa({\bf A})$, i.e., some singular values of ${\bf A}$ may be close to zero and the corresponding singular values of ${\bf A}^-$ may be very large. As the result, the approximated solution may be very large, and prone to noise. Such a system is said to be ill-conditioned. In this case, to avoid large ${\bf x}$, we can impose a penalty term $\alpha\vert\vert{\bf x}\vert\vert^2/2$ in the error function:

$$\varepsilon({\bf x}) =\frac{1}{2}\left( {\bf b}^T{\bf b}-{\bf x}^... ... b} -{\bf b}^T{\bf Ax}+{\bf x}^T{\bf A}^T{\bf Ax}+\alpha{\bf x}^T{\bf x}\right)$$ (126)

where $\alpha$ is a parameter that adjusts how tightly the size of ${\bf x}$ is controlled. Then repeating the process above we get:

$$\frac{\partial c({\bf x})}{\partial x_k} =-{\bf A}^T{\bf b}+{\bf A}^T{\bf Ax}+\alpha{\bf x}=0$$ (127)

which yields

$$({\bf A}^T{\bf A}+\alpha{\bf I}){\bf x}={\bf A}^T{\bf b}$$ (128)

Solving this for ${\bf x}$ we get:

$${\bf x}=({\bf A}^T{\bf A}+\alpha{\bf I})^{-1}{\bf A}^T{\bf b}$$ (129)

Consider the following two linear equation ssytems:

$$\left\{\begin{array}{l} x+y+z=1 \\ x+y+z=2 \end{array}\right.,\;\... ...egin{array}{l} x+y=2\nonumber \\ 2x+2y=4\nonumber \\ 3x+3y=6 \end{array}\right.$$

In the first system, there are fewer equations than unknowns ($M<N$), but there exist no solution; in the second system, there are more equations than unknowns ($M>N$), but there exist infinite number of solutions. We therefore see that in general, if a linear system has no solution, unique solution, or multiple solutions can not be determined simply by checking if $M>N$, $M=N$, or $M<N$. This issue of the stucture of the solution set of a linear equation system ${\bf Ax}={\bf b}$ can be fully addressed by the Fundamental Theorem of Linear Algebra discussed below.

The second system above can be solved by the pseudo inverse methed:

$${\bf A}=\left[\begin{array}{cc}1&1\\ 2&2\\ 3&3\end{array}\right],... ...=2\left[\begin{array}{ccc} 1 & 2 & 3\\ 2 & 4 & 6 \\ 3 & 6 & 9\end{array}\right]$$ (130)

We see that ${\bf A}^T{\bf A}$ is a singular and not invertible, and we cannot get the pseudo inverse by ${\bf A}^-=({\bf A}^T{\bf A})^{-1}{\bf A}^T$. However, we can still find the pseudo inverse of ${\bf A}$ by SVD method ${\bf A}={\bf U\Sigma V}^T$ with:

$${\bf U}=\left[\begin{array}{rrr} 0.2673 & -0.9482 & -0.1719 \\ 0... ... V}=\frac{1}{\sqrt{2}}\left[\begin{array}{rr} 1 & 1 \\ 1 &-1 \end{array}\right]$$ (131)

and

$${\bf A}^-={\bf V\Sigma}^-{\bf U}^T =\left[\begin{array}{rrr}0.0357 & 0.0714 & 0.1071\\ 0.0357 & 0.0714 & 0.1071\end{array}\right]$$ (132)

Now we can find the solution:

$${\bf x}={\bf A}^-{b}=\left[\begin{array}{c}1\\ 1\end{array}\right]$$ (133)