In the previous section we obtained the solution of the equation
 together with the bases of the four subspaces
of
together with the bases of the four subspaces
of  based its rref. Here we will consider an alternative
and better way to solve the same equation and find a set of
orthogonal bases that also span the four subspaces, based on the
pseudo-inverse
and
the singular value decomposition (SVD)
of
based its rref. Here we will consider an alternative
and better way to solve the same equation and find a set of
orthogonal bases that also span the four subspaces, based on the
pseudo-inverse
and
the singular value decomposition (SVD)
of  . The solution obtained this
way is optimal in some certain sense as shown below.
. The solution obtained this
way is optimal in some certain sense as shown below.
Consider the SVD of an  matrix
matrix  of rank
of rank
 :
:
 |
(160) |
where
![$\displaystyle {\bf\Sigma}=\left[\begin{array}{cccccc}\sigma_1&&&&&0\\
&\ddots&...
...&&\sigma_R &&&\\ &&&0&&\\ &&&&\ddots &\\ 0&&&&&0
\end{array}\right]_{M\times N}$](img622.svg) |
(161) |
is an  matrix with
matrix with  non-zero singular values
non-zero singular values
 of
of  along
the diagonal (starting from the top-left corner), while all other
components are zero, and
along
the diagonal (starting from the top-left corner), while all other
components are zero, and
![${\bf U}=[{\bf u}_1,\cdots,{\bf u}_M]$](img624.svg) and
and
![${\bf V}=[{\bf v}_1,\cdots,{\bf v}_N]$](img625.svg) are two orthogonal matrices
of dimensions
are two orthogonal matrices
of dimensions  and
and  respectively. The column
vectors
respectively. The column
vectors
 and
and
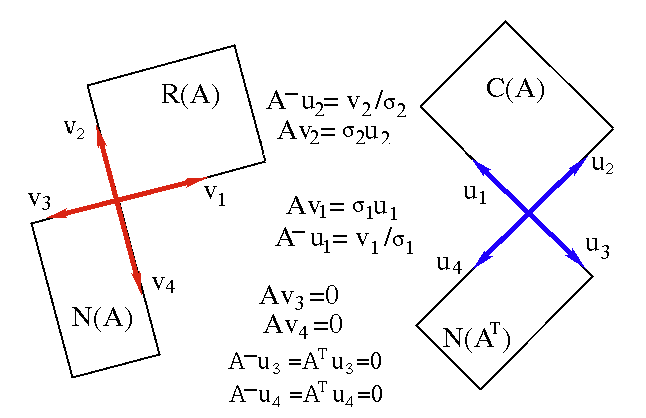
 ,
are called the left and right singular vectors of
,
are called the left and right singular vectors of  ,
respectively, and they can be used as the orthonormal bases to span
respectively
,
respectively, and they can be used as the orthonormal bases to span
respectively
 and its
subspaces
and its
subspaces
 and
and
 , and
, and
 and its subspaces
and its subspaces
 and
and
 .
.
To see this, we rewrite the SVD of  as:
as:
Each column vector of  can be expressed as a linear
combination of the first
can be expressed as a linear
combination of the first  columns of
columns of  corresponding
to the non-zero singular values:
corresponding
to the non-zero singular values:
 |
(163) |
Taking transpose on both sides of the SVD we also get:
i.e., each row vector of  can be expressed as a linear
combination of the first
can be expressed as a linear
combination of the first  columns of
columns of  corresponding
to the non-zero singular values:
corresponding
to the non-zero singular values:
 |
(165) |
We therefore see that the  columns of
columns of  and
and  corresponding to the non-zero singular values span respectively
the column space
corresponding to the non-zero singular values span respectively
the column space
 and row space
and row space
 :
:
 |
(166) |
and the remaining  columns of
columns of  and
and  columns of
columns of
 corresponding to the zero singular values span respectively
corresponding to the zero singular values span respectively
 orthogonal to
orthogonal to
 , and
, and
 orthogonal
to
orthogonal
to
 :
:
 |
(167) |
| Subspace |
Definition |
Dimension |
Basis |
 |
column space (image) of  |
 |
 columns of columns of  corresponding to non-zero singular values corresponding to non-zero singular values |
 |
left null space of  |
 |
 columns of columns of  corresponding to zero singular values corresponding to zero singular values |
 |
row space of  (column space of (column space of  ) ) |
 |
 columns of columns of  corresponding to non-zero singular values corresponding to non-zero singular values |
 |
null space of  |
 |
 columns of columns of  corresponding to zero singular values corresponding to zero singular values |
 |
domain of
 |
 |
all  columns of columns of  |
 |
codomain of
 |
 |
all  columns of columns of  |
The SVD method can be used to find the pseudo-inverse of an  matrix
matrix  of rank
of rank
 :
:
 |
(168) |
where both  and
and
![$\displaystyle {\bf\Sigma}^-=\left[\begin{array}{cccccc}1/\sigma_1&&&&&0\\
&\dd...
...1/\sigma_R &&&\\ &&&0&&\\ &&&&\ddots &\\ 0&&&&&0
\end{array}\right]_{N\times M}$](img650.svg) |
(169) |
are  matrices.
matrices.
Consider the following four cases:
- If
 , then
, then
 ,
,
 .
.
- If
 , then
, then
 (full rank),
(full rank),  is a left inverse:
is a left inverse:
 |
(170) |
However,
 |
(171) |
as the  matrix
matrix
 with only
with only  1's
along the diagonal is not full rank and unequal to
1's
along the diagonal is not full rank and unequal to
 ,
,
- If
 , the
, the
 (full rank),
(full rank),  is a right inverse:
is a right inverse:
 |
(172) |
However,
 |
(173) |
as the  matrix
matrix
 with only
with only  1's
along the diagonal is not a full rank identity matrix
1's
along the diagonal is not a full rank identity matrix
 .
.
- If
 , then neither
, then neither
 nor
nor
 is full rank, as they only have
is full rank, as they only have  non-zeros 1's along the diagonal, therefore
non-zeros 1's along the diagonal, therefore  is neither
left nor right inverse:
is neither
left nor right inverse:
 |
(174) |
We further note that matrices  and
and  are related to each
other by:
are related to each
other by:
 or or |
(175) |
or in vector form:
 |
(176) |
indicating how the individual columns are related.
We see that the last  columns
columns
 of
of
 form an orthogonal basis of
form an orthogonal basis of
 ; and the last
; and the last  columns
columns
 of
of  form an orthogonal
basis of
form an orthogonal
basis of
 .
.
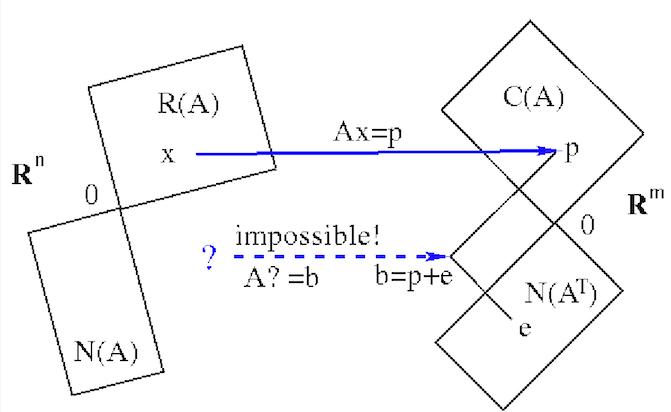
We now show that the optimal solution of the linear system
 can be obtained based on the pseudo-inverse
of
can be obtained based on the pseudo-inverse
of  :
:
 |
(177) |
Specially, if  , then
, then
 , and
, and
 is the unique and exact solution.
In general when
is the unique and exact solution.
In general when  or
or
 , the solution may not
exist, or it may not be unique, but
, the solution may not
exist, or it may not be unique, but
 is still an
optimal solution in two ways, from the perspective of both the
domain and codomain of the linear mapping
is still an
optimal solution in two ways, from the perspective of both the
domain and codomain of the linear mapping  , as shown below.
, as shown below.
- In domain
 :
:
Pre-multiplying
 on both sides of the
pseudo-inverse solution
on both sides of the
pseudo-inverse solution
 given above,
we get:
given above,
we get:
![$\displaystyle {\bf V}^T{\bf x}_{svd}
=[{\bf v}_1,\cdots,{\bf v}_N]^T{\bf x}_{sv...
...f\Sigma}^-{\bf U}^T{\bf b}
={\bf\Sigma}^-[{\bf u}_1,\cdots,{\bf u}_M]^T{\bf b},$](img677.svg) |
(178) |
or in component form:
![$\displaystyle \left[\begin{array}{c}{\bf v}_1^T{\bf x}_{svd}\\ \vdots\\
{\bf v...
...ma_1\\ \vdots\\
{\bf u}_R^T{\bf b}/\sigma_R\\ 0\\ \vdots\\ 0\end{array}\right]$](img678.svg) |
(179) |
- The first
 components
components
 are the projection of
are the projection of
 onto
onto
 spanned by
spanned by
 corresponding to the non-zero
singular values;
corresponding to the non-zero
singular values;
- The last
 components
components
 are the projection
of
are the projection
of
 onto
onto
 spanned by
spanned by
 corresponding to the zero
singular values.
corresponding to the zero
singular values.
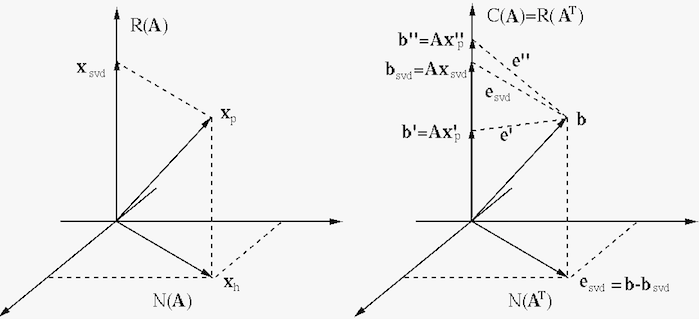
We see that
 is entirely in the row space,
containing no homogeneous component in
is entirely in the row space,
containing no homogeneous component in
 , i.e.,
, i.e.,
 has the minimum norm (closest to the origin) compared to any other possible
solution
has the minimum norm (closest to the origin) compared to any other possible
solution  , such as those found previously based on the rref
of
, such as those found previously based on the rref
of  , containing a non-zero homogeneous component
, containing a non-zero homogeneous component
 :
:
 |
(180) |
As
 ,
,
 is the
projection of any such solution
is the
projection of any such solution  onto
onto
 . The
complete solution can be found as
. The
complete solution can be found as
 |
(181) |
for any set of coefficients  .
.
- In codomain
 :
:
We now consider the result
 produced
by the pseudo-inverse solution
produced
by the pseudo-inverse solution
 , which, as a linear
combination of the columns of
, which, as a linear
combination of the columns of  , is in its column space
, is in its column space
 :
:
 |
(182) |
Pre-multiplying
 on both sides we get:
on both sides we get:
 |
(183) |
or in component form:
![$\displaystyle \left[\begin{array}{c}{\bf u}_1^T{\bf b}_{svd}\\ \vdots\\
{\bf u...
...u}_1^T{\bf b}\\ \vdots\\
{\bf u}_R^T{\bf b}\\ 0\\ \vdots\\ 0\end{array}\right]$](img691.svg) |
(184) |
We see that
 is entirely in the column
space. If
is entirely in the column
space. If
 , then
, then
 is an
exact solution. But if
is an
exact solution. But if
 , then
, then
 and
and
 is not an exact solution.
But as
is not an exact solution.
But as
 is the projection of
is the projection of  onto
onto
 , the error
, the error
 is minimized in
comparison to any other possible
is minimized in
comparison to any other possible

 |
(185) |
We therefore see that
 is the optimal solution.
is the optimal solution.
Summarizing the two aspects above, we see that the pseudo-inverse
solution
 is optimal in the sense that both its
norm
is optimal in the sense that both its
norm
 and its error
and its error
 are minimized.
are minimized.
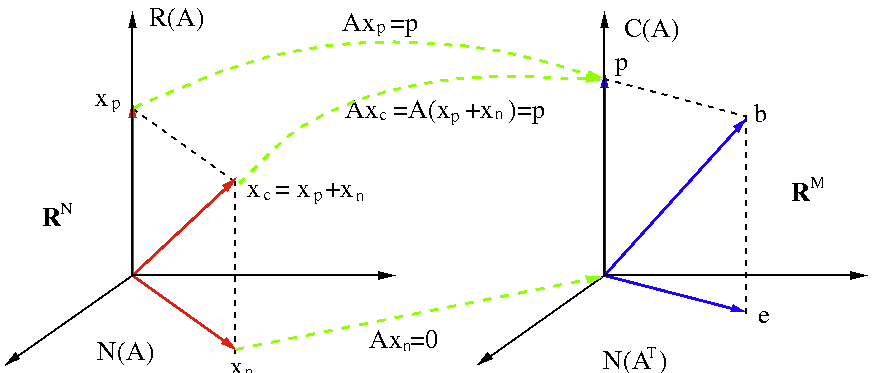
- If the solution
 is not unique because
is not unique because
 , then the complete solution can be
found by adding the entire null space to it:
, then the complete solution can be
found by adding the entire null space to it:
 .
.
- If no solution exists because
 ,
then
,
then
 is the optimal approximate solution with
minimum error.
is the optimal approximate solution with
minimum error.
Example: Given the same system considered in previous examples
we will now solve it using the pseudo-inverse method. We first find SVD of
 in terms of the following matrices:
in terms of the following matrices:
The particular solution of the system
 with
with
![${\bf b}=[3,\;2,\;4]^T\in C({\bf A})$](img713.svg) is
is
which is in
 spanned by the first
spanned by the first  columns
columns
 and
and  , perpendicular to
, perpendicular to
 spanned
by the last
spanned
by the last  columns
columns  and
and  . Note that
this solution
. Note that
this solution
![${\bf x}_{svd}=[0.1,\;0.2,\;0.3,\;0.4]^T$](img721.svg) is actually
the first component
is actually
the first component
 of the particular
solution
of the particular
solution
![${\bf x}_p=[-1,\,2,\,0,\,0]$](img723.svg) found in the previous section
by Gauss-Jordan elimination, which is not in
found in the previous section
by Gauss-Jordan elimination, which is not in
 . Adding the
null space to the particular solution, we get the complete solution:
If the right-hand side is replaced by
. Adding the
null space to the particular solution, we get the complete solution:
If the right-hand side is replaced by
![${\bf b}=[1,\;3,\;5]^T\notin C({\bf A})$](img599.svg) , no solution exists. However, we can still find the
pseudo-inverse solution as the optimal approximate solution:
which is the same as the solution for
, no solution exists. However, we can still find the
pseudo-inverse solution as the optimal approximate solution:
which is the same as the solution for
![${\bf b}=[3,\;2,\;4]^T$](img726.svg) ,
indicating
,
indicating
![$[3,\;2,\;4]^T$](img727.svg) happens to be the projection of
happens to be the projection of
![$[1,\;3,\;5]^T$](img728.svg) onto
onto
 spanned by
spanned by  and
and
 . The result produced by
. The result produced by
 is
is
 is the projection of
is the projection of
 onto
onto
 , with a minimum error distance
, with a minimum error distance
 , indicating
, indicating
 is the optimal approximate solution.
is the optimal approximate solution.
Homework 3:
- Use Matlab function
svd(A) to carry out the SVD of the coefficient
matrix  of the linear system in Homework 2 problem 3,
Find
of the linear system in Homework 2 problem 3,
Find  ,
,  ,
,
 . Verify that
. Verify that  and
and
 are orthogonal, i.e.,
are orthogonal, i.e.,
 and
and
 .
.
- Obtain
 , i.e, find the transpose of
, i.e, find the transpose of
 and then replace each singular value by its reciprocal, verify that
and then replace each singular value by its reciprocal, verify that
 and
and
 .
Then find the pseudo-inverse
.
Then find the pseudo-inverse
 .
.
- Use Matlab function
pinv(A) to find the pseudo-inverse
 and
and  . Compare them to what you obtained
in the previous part.
. Compare them to what you obtained
in the previous part.
- Identify the bases of the four subspaces
 ,
,
 ,
,
 , and
, and
 based on
based on  and
and
 . Verify that these bases and those you found previously (problem
3 of Homework 2) span the same spaces, i.e., the basis vectors of one basis
can be written as a linear combination of those of the other, for each of
the four subspaces.
. Verify that these bases and those you found previously (problem
3 of Homework 2) span the same spaces, i.e., the basis vectors of one basis
can be written as a linear combination of those of the other, for each of
the four subspaces.
- Use the pseudo-inverse
 found above to solve
the system
found above to solve
the system
 . Find the two particular solutions
. Find the two particular solutions
 and
and
 corresponding to two different right-hand
side
corresponding to two different right-hand
side
![${\bf b}_1=[1,\;2,\;3]^T$](img742.svg) and
and
![${\bf b}_2=[2,\;3,\;2]^T$](img743.svg) .
.
- How are the two results
 and
and
 related to
each other? Give your explanation. Why can't you find a solution when
related to
each other? Give your explanation. Why can't you find a solution when
![${\bf b}=[2,\;3,\;2]^T$](img744.svg) but SVD method can?
but SVD method can?
- Verify that
 . Also find the error (or
residual)
. Also find the error (or
residual)
 for each of the two results
above. Verify that
for each of the two results
above. Verify that
 , if
, if
 .
.
- In Homework 2 you used row reduction method to solve the system
 and you should have found a particular solution
and you should have found a particular solution
![${\bf x}_1=[5,\;2,\;0,\;0,\;]^T$](img750.svg) . Also it is obvious to see that another
solution is
. Also it is obvious to see that another
solution is
![${\bf x}_2=[0,\;0,\;0,\;1]^T$](img751.svg) . Show that the projection of
these solutions onto
. Show that the projection of
these solutions onto
 spanned by the first two columns of
spanned by the first two columns of
 is the same as the particular solution
is the same as the particular solution  found by
the SVD method.
found by
the SVD method.
Answer
- Show that
![${\bf b}_1=[1,\;2,\;3]^T$](img742.svg) is the projection of
is the projection of
![${\bf b}_2=[2,\;3,\;2]^T$](img743.svg) onto
onto
 , the 2-D subspace spanned by
the first two columns of
, the 2-D subspace spanned by
the first two columns of  . Can you also show that it is the
projection of
. Can you also show that it is the
projection of  onto
onto
 spanned by the basis you obtained
in Homework 2 (not necessarily orthogonal)?
spanned by the basis you obtained
in Homework 2 (not necessarily orthogonal)?
Answer
- Give an expression of the null space
 , and then write the
complete solution in form of
, and then write the
complete solution in form of
 . Verify any
complete solution so generated satisfies
. Verify any
complete solution so generated satisfies
 .
.







![$\displaystyle {\bf\Sigma}=\left[\begin{array}{cccccc}\sigma_1&&&&&0\\
&\ddots&...
...&&\sigma_R &&&\\ &&&0&&\\ &&&&\ddots &\\ 0&&&&&0
\end{array}\right]_{M\times N}$](img622.svg)
 matrix with
matrix with  non-zero singular values
non-zero singular values
 of
of  along
the diagonal (starting from the top-left corner), while all other
components are zero, and
along
the diagonal (starting from the top-left corner), while all other
components are zero, and
![${\bf U}=[{\bf u}_1,\cdots,{\bf u}_M]$](img624.svg) and
and
![${\bf V}=[{\bf v}_1,\cdots,{\bf v}_N]$](img625.svg) are two orthogonal matrices
of dimensions
are two orthogonal matrices
of dimensions  and
and  respectively. The column
vectors
respectively. The column
vectors
 and
and
 ,
are called the left and right singular vectors of
,
are called the left and right singular vectors of  ,
respectively, and they can be used as the orthonormal bases to span
respectively
,
respectively, and they can be used as the orthonormal bases to span
respectively
 and its
subspaces
and its
subspaces
 and
and
 , and
, and
 and its subspaces
and its subspaces
 and
and
 .
.



![$\displaystyle [{\bf c}_1,\cdots,{\bf c}_N]={\bf U\Sigma V}^T$](img631.svg)

![$\displaystyle [{\bf u}_1,\cdots\cdots\cdots,{\bf u}_M]
\left[\begin{array}{cccc...
...array}{c}{\bf v}_1^T\\ \vdots\\ \vdots\\ \vdots\\ {\bf v}_N^T\end{array}\right]$](img632.svg)

![$\displaystyle \sum_{k=1}^R \sigma_k\;\left({\bf u}_k{\bf v}_k^T\right)
=\sum_{k...
...gma_kv_{1k})\;{\bf u}_k,\cdots,
\sum_{k=1}^R (\sigma_kv_{Nk})\;{\bf u}_k\right]$](img633.svg)
 can be expressed as a linear
combination of the first
can be expressed as a linear
combination of the first  columns of
columns of  corresponding
to the non-zero singular values:
corresponding
to the non-zero singular values:



![$\displaystyle [{\bf r}_1,\cdots,{\bf r}_M]
={\bf V\Sigma}^T{\bf U}^T$](img637.svg)

![$\displaystyle \sum_{k=1}^R \sigma_k\;\left({\bf v}_k{\bf u}_k^T\right)
=\sum_{k...
...ku_{1k})\;{\bf v}_k,\;\cdots,\;
\sum_{k=1}^R (\sigma_ku_{Mk})\;{\bf v}_k\right]$](img638.svg)
 can be expressed as a linear
combination of the first
can be expressed as a linear
combination of the first  columns of
columns of  corresponding
to the non-zero singular values:
corresponding
to the non-zero singular values:

 columns of
columns of  and
and  corresponding to the non-zero singular values span respectively
the column space
corresponding to the non-zero singular values span respectively
the column space
 and row space
and row space
 :
:

 columns of
columns of  and
and  columns of
columns of
 corresponding to the zero singular values span respectively
corresponding to the zero singular values span respectively
 orthogonal to
orthogonal to
 , and
, and
 orthogonal
to
orthogonal
to
 :
:




 columns of
columns of  corresponding to non-zero singular values
corresponding to non-zero singular values


 columns of
columns of  corresponding to zero singular values
corresponding to zero singular values
 (column space of
(column space of  )
)
 columns of
columns of  corresponding to non-zero singular values
corresponding to non-zero singular values


 columns of
columns of  corresponding to zero singular values
corresponding to zero singular values


 columns of
columns of 



 columns of
columns of 




 and
and
![$\displaystyle {\bf\Sigma}^-=\left[\begin{array}{cccccc}1/\sigma_1&&&&&0\\
&\dd...
...1/\sigma_R &&&\\ &&&0&&\\ &&&&\ddots &\\ 0&&&&&0
\end{array}\right]_{N\times M}$](img650.svg)
 matrices.
matrices.
 , then
, then
 ,
,
 .
.
 , then
, then
 (full rank),
(full rank),  is a left inverse:
is a left inverse:


 matrix
matrix
 with only
with only  1's
along the diagonal is not full rank and unequal to
1's
along the diagonal is not full rank and unequal to
 ,
,
 , the
, the
 (full rank),
(full rank),  is a right inverse:
is a right inverse:


 matrix
matrix
 with only
with only  1's
along the diagonal is not a full rank identity matrix
1's
along the diagonal is not a full rank identity matrix
 .
.
 , then neither
, then neither
 nor
nor
 is full rank, as they only have
is full rank, as they only have  non-zeros 1's along the diagonal, therefore
non-zeros 1's along the diagonal, therefore  is neither
left nor right inverse:
is neither
left nor right inverse:



 or
or

 columns
columns
 of
of
 form an orthogonal basis of
form an orthogonal basis of
 ; and the last
; and the last  columns
columns
 of
of  form an orthogonal
basis of
form an orthogonal
basis of
 .
.




 , then
, then
 , and
, and
 is the unique and exact solution.
In general when
is the unique and exact solution.
In general when  or
or
 , the solution may not
exist, or it may not be unique, but
, the solution may not
exist, or it may not be unique, but
 is still an
optimal solution in two ways, from the perspective of both the
domain and codomain of the linear mapping
is still an
optimal solution in two ways, from the perspective of both the
domain and codomain of the linear mapping  , as shown below.
, as shown below.
 :
:


![$\displaystyle {\bf V}^T{\bf x}_{svd}
=[{\bf v}_1,\cdots,{\bf v}_N]^T{\bf x}_{sv...
...f\Sigma}^-{\bf U}^T{\bf b}
={\bf\Sigma}^-[{\bf u}_1,\cdots,{\bf u}_M]^T{\bf b},$](img677.svg)
![$\displaystyle \left[\begin{array}{c}{\bf v}_1^T{\bf x}_{svd}\\ \vdots\\
{\bf v...
...ma_1\\ \vdots\\
{\bf u}_R^T{\bf b}/\sigma_R\\ 0\\ \vdots\\ 0\end{array}\right]$](img678.svg)
 components
components
 are the projection of
are the projection of
 onto
onto
 spanned by
spanned by
 corresponding to the non-zero
singular values;
corresponding to the non-zero
singular values;
 components
components
 are the projection
of
are the projection
of
 onto
onto
 spanned by
spanned by
 corresponding to the zero
singular values.
corresponding to the zero
singular values.
 is entirely in the row space,
containing no homogeneous component in
is entirely in the row space,
containing no homogeneous component in
 , i.e.,
, i.e.,
 has the minimum norm (closest to the origin) compared to any other possible
solution
has the minimum norm (closest to the origin) compared to any other possible
solution  , such as those found previously based on the rref
of
, such as those found previously based on the rref
of  , containing a non-zero homogeneous component
, containing a non-zero homogeneous component
 :
:

 ,
,
 is the
projection of any such solution
is the
projection of any such solution  onto
onto
 . The
complete solution can be found as
. The
complete solution can be found as

 .
.
 :
:





 on both sides we get:
on both sides we get:

![$\displaystyle \left[\begin{array}{c}{\bf u}_1^T{\bf b}_{svd}\\ \vdots\\
{\bf u...
...u}_1^T{\bf b}\\ \vdots\\
{\bf u}_R^T{\bf b}\\ 0\\ \vdots\\ 0\end{array}\right]$](img691.svg)
 components
components
 ,
i.e.,
,
i.e.,
 and
and  have the same projection onto
have the same projection onto
 spanned by
spanned by
 corresponding
to the non-zero singular values.
corresponding
to the non-zero singular values.
 components
components
 are the projection
of
are the projection
of
 onto
onto
 spanned by
spanned by
 corresponding to the zero
singular values.
corresponding to the zero
singular values.












 is the optimal solution.
is the optimal solution.



 is not unique because
is not unique because
 , then the complete solution can be
found by adding the entire null space to it:
, then the complete solution can be
found by adding the entire null space to it:
 .
.
 ,
then
,
then
 is the optimal approximate solution with
minimum error.
is the optimal approximate solution with
minimum error.



![$\displaystyle {\bf A}{\bf x}=\left[\begin{array}{rccc}1&2&3&4\\ 4&3&2&1\\ -2&1&...
... x_3\\ x_4\end{array}\right]
=\left[\begin{array}{r}3\\ 2\\ 4\end{array}\right]$](img706.svg)
 in terms of the following matrices:
in terms of the following matrices:
![$\displaystyle {\bf U}=[{\bf u}_1,\;{\bf u}_2,\;{\bf u}_3]
=\left[\begin{array}{...
...817 \\
-0.267 & -0.873 & -0.408 \\
-0.802 & 0.436 & -0.408 \end{array}\right]$](img707.svg)
![$\displaystyle {\bf V}=[{\bf v}_1,\;{\bf v}_2,\;{\bf v}_3,\;{\bf v}_4]
=\left[\b...
... -0.120 & 0.472 & 0.691 \\
-0.802 & 0.239 & -0.049 & -0.546 \end{array}\right]$](img708.svg)
![$\displaystyle {\bf\Sigma}=\left[\begin{array}{cccc}
10.0 & 0 & 0 & 0 \\
0 & 5....
...c}
0.1 & 0 & 0 \\
0 & 0.183 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \end{array}\right]$](img709.svg)


![$\displaystyle \left[\begin{array}{rrrr}
0.000 & -0.837 & 0.374 & -0.400 \\
-0....
....802 \\
-0.218 & -0.873 & 0.436 \\
0.817 & -0.408 & -0.408 \end{array}\right]$](img711.svg)

![$\displaystyle \left[\begin{array}{rrr}
0.033 & 0.133 & -0.067 \\
0.033 & 0.083 & -0.017 \\
0.033 & 0.033 & 0.033 \\
0.033 & -0.017 & 0.083 \end{array}\right]$](img712.svg)
 with
with
![${\bf b}=[3,\;2,\;4]^T\in C({\bf A})$](img713.svg) is
is


![$\displaystyle {\bf A}^-{\bf b}=\left[\begin{array}{rrr}
0.033 & 0.133 & -0.067 ...
...nd{array}\right]
=\left[\begin{array}{r}0.1\\ 0.2\\ 0.3\\ 0.4\end{array}\right]$](img715.svg)

![$\displaystyle -0.535\left[\begin{array}{r}0.000\\ -0.267\\ -0.535\\ -0.802\end{...
...r}-0.837\\ -0.478\\ -0.120\\ 0.239\end{array}\right]
=c_1{\bf v}_1+c_2{\bf v}_2$](img716.svg)
 spanned by the first
spanned by the first  columns
columns
 and
and  , perpendicular to
, perpendicular to
 spanned
by the last
spanned
by the last  columns
columns  and
and  . Note that
this solution
. Note that
this solution
![${\bf x}_{svd}=[0.1,\;0.2,\;0.3,\;0.4]^T$](img721.svg) is actually
the first component
is actually
the first component
 of the particular
solution
of the particular
solution
![${\bf x}_p=[-1,\,2,\,0,\,0]$](img723.svg) found in the previous section
by Gauss-Jordan elimination, which is not in
found in the previous section
by Gauss-Jordan elimination, which is not in
 . Adding the
null space to the particular solution, we get the complete solution:
. Adding the
null space to the particular solution, we get the complete solution:
![$\displaystyle {\bf x}_c={\bf x}_{svd}+N({\bf A})={\bf x}_p+c_1{\bf v}_3+c_2{\bf...
...t]
+c_2 \left[\begin{array}{r}-0.400\\ 0.255\\ 0.691\\ -0.546\end{array}\right]$](img724.svg)
![${\bf b}=[1,\;3,\;5]^T\notin C({\bf A})$](img599.svg) , no solution exists. However, we can still find the
pseudo-inverse solution as the optimal approximate solution:
, no solution exists. However, we can still find the
pseudo-inverse solution as the optimal approximate solution:
![$\displaystyle {\bf x}_{svd}={\bf A}^-{\bf b}=\left[\begin{array}{rrr}
0.033 & 0...
...nd{array}\right]
=\left[\begin{array}{r}0.1\\ 0.2\\ 0.3\\ 0.4\end{array}\right]$](img725.svg)
![${\bf b}=[3,\;2,\;4]^T$](img726.svg) ,
indicating
,
indicating
![$[3,\;2,\;4]^T$](img727.svg) happens to be the projection of
happens to be the projection of
![$[1,\;3,\;5]^T$](img728.svg) onto
onto
 spanned by
spanned by  and
and
 . The result produced by
. The result produced by
 is
is
 is the projection of
is the projection of
 onto
onto
 , with a minimum error distance
, with a minimum error distance
 , indicating
, indicating
 is the optimal approximate solution.
is the optimal approximate solution.
 of the linear system in Homework 2 problem 3,
of the linear system in Homework 2 problem 3,
![$\displaystyle {\bf A}=\left[\begin{array}{rrrr}-1 & 3 & 4 & 1\\
2 & -4 & 3 & 2\\ 1 & -1 & 7 & 3\end{array}\right]$](img733.svg)
 ,
,  ,
,
 . Verify that
. Verify that  and
and
 are orthogonal, i.e.,
are orthogonal, i.e.,
 and
and
 .
.
 , i.e, find the transpose of
, i.e, find the transpose of
 and then replace each singular value by its reciprocal, verify that
and then replace each singular value by its reciprocal, verify that
 and
and
 .
Then find the pseudo-inverse
.
Then find the pseudo-inverse
 .
.
 and
and  . Compare them to what you obtained
in the previous part.
. Compare them to what you obtained
in the previous part.
 ,
,
 ,
,
 , and
, and
 based on
based on  and
and
 . Verify that these bases and those you found previously (problem
3 of Homework 2) span the same spaces, i.e., the basis vectors of one basis
can be written as a linear combination of those of the other, for each of
the four subspaces.
. Verify that these bases and those you found previously (problem
3 of Homework 2) span the same spaces, i.e., the basis vectors of one basis
can be written as a linear combination of those of the other, for each of
the four subspaces.
 found above to solve
the system
found above to solve
the system
 . Find the two particular solutions
. Find the two particular solutions
 and
and
 corresponding to two different right-hand
side
corresponding to two different right-hand
side
![${\bf b}_1=[1,\;2,\;3]^T$](img742.svg) and
and
![${\bf b}_2=[2,\;3,\;2]^T$](img743.svg) .
.
 and
and
 related to
each other? Give your explanation. Why can't you find a solution when
related to
each other? Give your explanation. Why can't you find a solution when
![${\bf b}=[2,\;3,\;2]^T$](img744.svg) but SVD method can?
but SVD method can?
 . Also find the error (or
residual)
. Also find the error (or
residual)
 for each of the two results
above. Verify that
for each of the two results
above. Verify that
 , if
, if
 .
.
 and you should have found a particular solution
and you should have found a particular solution
![${\bf x}_1=[5,\;2,\;0,\;0,\;]^T$](img750.svg) . Also it is obvious to see that another
solution is
. Also it is obvious to see that another
solution is
![${\bf x}_2=[0,\;0,\;0,\;1]^T$](img751.svg) . Show that the projection of
these solutions onto
. Show that the projection of
these solutions onto
 spanned by the first two columns of
spanned by the first two columns of
 is the same as the particular solution
is the same as the particular solution  found by
the SVD method.
found by
the SVD method.




![${\bf b}_1=[1,\;2,\;3]^T$](img742.svg) is the projection of
is the projection of
![${\bf b}_2=[2,\;3,\;2]^T$](img743.svg) onto
onto
 , the 2-D subspace spanned by
the first two columns of
, the 2-D subspace spanned by
the first two columns of  . Can you also show that it is the
projection of
. Can you also show that it is the
projection of  onto
onto
 spanned by the basis you obtained
in Homework 2 (not necessarily orthogonal)?
spanned by the basis you obtained
in Homework 2 (not necessarily orthogonal)?

![$\displaystyle c_1{\bf u}_1+c_2{\bf u}_2=[1,\;2,\;3]^T={\bf b}_1$](img757.svg)
 , and then write the
complete solution in form of
, and then write the
complete solution in form of
 . Verify any
complete solution so generated satisfies
. Verify any
complete solution so generated satisfies
 .
.