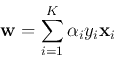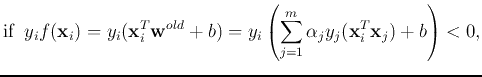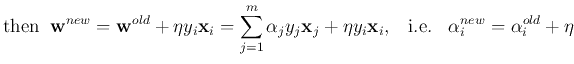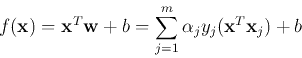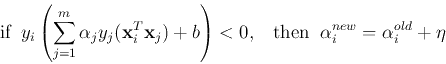Next: Support Vector Machine
Up: Support Vector Machines (SVM)
Previous: Linear separation of a
Given a set 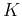 training samples from two linearly separable classes P and N:
training samples from two linearly separable classes P and N:
where
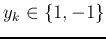 labels
labels 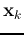 to belong to either of the two
classes. we want to find a hyper-plane in terms of
to belong to either of the two
classes. we want to find a hyper-plane in terms of 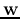 and
and 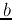 , that
linearly separates the two classes.
, that
linearly separates the two classes.
Before the classifier is properly trained, the actual output
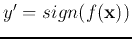 may not be the same as the desired output
may not be the same as the desired output 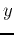 . There are four possible cases:
. There are four possible cases:
The weight vector 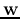 is updated whenever the result is incorrect (mistake
driven):
is updated whenever the result is incorrect (mistake
driven):
- If
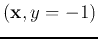 but
but 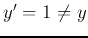 (case 2 above), then
(case 2 above), then
When the same 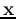 is presented again, we have
is presented again, we have
The output
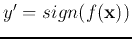 is more likely to be
is more likely to be 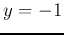 as desired.
Here
as desired.
Here 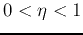 is the learning rate.
is the learning rate.
- If
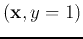 but
but 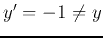 (case 3 above), then
(case 3 above), then
When the same 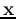 is presented again, we have
is presented again, we have
The output
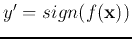 is more likely to be
is more likely to be 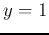 as desired.
as desired.
Summarizing the two cases, we get the learning law:
The two correct cases (cases 1 and 4) can also be summarized as
which is the condition a successful classifier should satisfy.
We assume initially 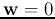 , and the
, and the 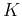 training samples are presented
repeatedly, the learning law during training will yield eventually:
training samples are presented
repeatedly, the learning law during training will yield eventually:
where 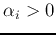 . Note that
. Note that 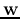 is expressed as a linear combination of
the training samples. After receiving a new sample
is expressed as a linear combination of
the training samples. After receiving a new sample
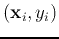 , vector
, vector
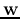 is updated by
is updated by
Now both the decision function
and the learning law
are expressed in terms of the inner production of input vectors.



Next: Support Vector Machine
Up: Support Vector Machines (SVM)
Previous: Linear separation of a
Ruye Wang
2016-08-24
![]() training samples from two linearly separable classes P and N:
training samples from two linearly separable classes P and N:
![]() may not be the same as the desired output
may not be the same as the desired output ![]() . There are four possible cases:
. There are four possible cases:
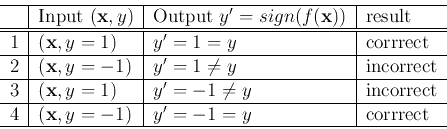
![]() is updated whenever the result is incorrect (mistake
driven):
is updated whenever the result is incorrect (mistake
driven):
![]() , and the
, and the ![]() training samples are presented
repeatedly, the learning law during training will yield eventually:
training samples are presented
repeatedly, the learning law during training will yield eventually: