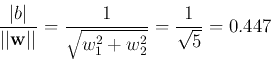Next: The learning problem
Up: Support Vector Machines (SVM)
Previous: Support Vector Machines (SVM)
A hyper plane in an n-D feature space can be represented by the following
equation:
Dividing by
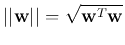 , we get
, we get
indicating that the projection of any point 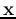 on the plane onto
the vector
on the plane onto
the vector 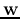 is always
is always
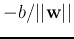 , i.e.,
, i.e., 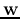 is the
normal direction of the plane, and
is the
normal direction of the plane, and
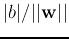 is the distance
from the origin to the plane. Note that the equation of the hyper plane
is not unique.
is the distance
from the origin to the plane. Note that the equation of the hyper plane
is not unique.
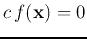 represents the same plane for any
represents the same plane for any 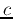 .
.
The n-D space is partitioned into two regions by the plane. Specifically,
we define a mapping function
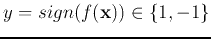 ,
,
Any point 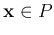 on the positive side of the plane is mapped to 1,
while any point
on the positive side of the plane is mapped to 1,
while any point 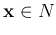 on the negative side is mapped to -1. A point
on the negative side is mapped to -1. A point
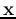 of unknown class will be classified to P if
of unknown class will be classified to P if 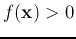 , or N if
, or N if
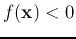 .
.
Example:
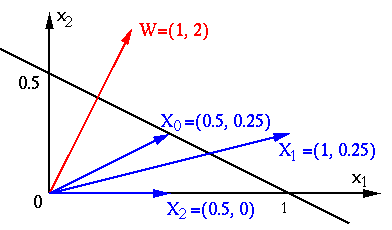
A straight line in 2D space
![${\bf x}=[x_1, x_2]^T$](img16.png) described by the following
equation:
described by the following
equation:
devides the 2D plane into two halves. The distance between the origin and the
line is
Consider three points:
-
![${\bf x}_0=[0.5,\;0.25]^T$](img19.png) ,
,
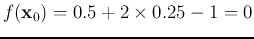 , i.e.,
, i.e.,
 is on the plane;
is on the plane;
-
![${\bf x}_1=[1,\;0.25]^T$](img22.png) ,
,
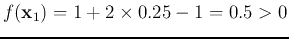 , i.e.,
, i.e.,
 is above the straight line;
is above the straight line;
-
![${\bf x}_2=[0.5,\;0]^T$](img25.png) ,
,
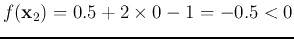 , i.e.,
, i.e.,
 is below the straight line.
is below the straight line.



Next: The learning problem
Up: Support Vector Machines (SVM)
Previous: Support Vector Machines (SVM)
Ruye Wang
2016-08-24
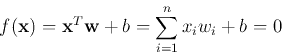
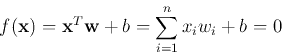
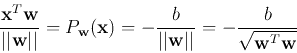
![]() ,
,
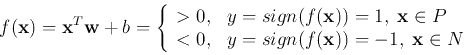

![]() described by the following
equation:
described by the following
equation:
![\begin{displaymath}
f({\bf x})={\bf x}^T {\bf w}+b=[x_1,x_2]
\left[ \begin{array...
...t[ \begin{array}{c} 1 2 \end{array} \right]-1
=x_1+2x_2-1=0 \end{displaymath}](img17.png)