Median Filter

Neighborhood averaging can suppress isolated out-of-range noise, but the side effect is that it also blurs sudden changes (corresponding to high spatial frequencies) such as sharp edges.

The median filter is an effective method that can suppress isolated noise without blurring sharp edges. Specifically, the median filter replaces a pixel by the median of all pixels in the neighborhood:

$$y[m,n]=median\{ x[i,j], (i,j) \in w \}$$

where $w$ represents a neighborhood centered around location $(mm,n)$ in the image.

1D median filter:

Consider a 1x5 window sliding over a 1D array (either horizontal or vertical) of pixels. Assume the five pixels currently inside the windows are:

where the middle pixel with value 200 is an isolated out-of-range noise. The median of these five values can be found by sorting the values (in either ascending or descending order). The middle value is the median:

The original pixel value 200 is replaced by the median 110.

Question: How do you get rid of noise in the form of horizontal line across the image using 1D median filter?

2D median filter:

The window of a 2D median filter can be of any central symmetric shape, a round disc, a square, a rectangle, or a cross. The pixel at the center will be replaced by the median of all pixel values inside the window.

Programming issues:

Sorting is necessary for finding the median of a set of values. There exit various sorting algorithm with complexity of $O(n\; log_2 n)$. However, in this case, as the number of pixels is quite limited, a simple sorting method with complexity $O(n^2)$ can be used. The code segment below sorts an array of k elements:

$$\par \; for (i=0;\;\; i<k-1;\;\; i++) \par \; for (j=i+1;\;\... ... \par \;\;\;\;\; \{ w=bin[i]; bin[i]=bin[j]; bin[j]=w; \} \par$$

Example:

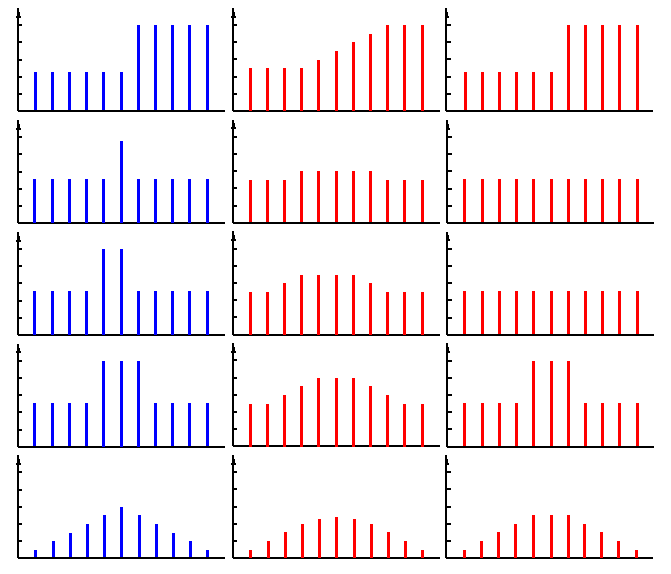
This figure shows the comparison of the smoothing results of a 1D signal (blue, 1st column) by an average filter (red, 2nd column) and by a median filter (red, 3rd column) both of size five. It is clear that the median filter preserves sharp edges while completely suppressing isolated out-of-range noise, so long as its size is less than half of the filter window size, while the average filter always blurs edges without completely suppressing noise. The median filter does not change any out-of-range spot more than half of the window size, as the spot is large enough to be some legitimate feature in the image.