


Next: About this document ...
Up: Smoothing
Previous: Median Filter
Statistical thresholding
First find the mean 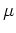 and the variance
and the variance 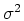 of all pixels
in the neighborhood
of all pixels
in the neighborhood 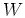 of a given pixel
of a given pixel ![$x[m,n]$](img16.png) of the input image:
of the input image:
where 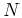 is the number of pixels in the neighborhood
is the number of pixels in the neighborhood 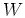 .
.
Then find the corresponding pixel for the output image:
where 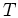 is a user specified threshold value.
is a user specified threshold value.
Nagao's algorithm
- Define a set of K neighborhoods around the pixel
![$x[m,n]$](img16.png) under consideration,
for example, the eight 3x3 neighborhoods in N, NE, E, SE, S, SW, W, and NW directions.
The pixel
under consideration,
for example, the eight 3x3 neighborhoods in N, NE, E, SE, S, SW, W, and NW directions.
The pixel ![$x[m,n]$](img16.png) should be included as a corner in each of these neighborhoods.
should be included as a corner in each of these neighborhoods.
- Find the mean
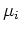 and variance
and variance 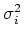 for each of the K neighborhoods.
for each of the K neighborhoods.
- Replace pixel
![$x[m,n]$](img16.png) by one of the means corresponding to the smallest
by one of the means corresponding to the smallest 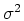 :
:
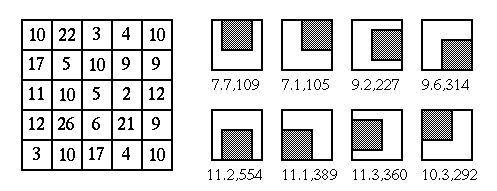
In this example, the pixel in question ![$x[m,n]=5$](img43.png) is replaced by the mean 7.1 from
the northeast neighborhood with minimum variance 105.
is replaced by the mean 7.1 from
the northeast neighborhood with minimum variance 105.



Next: About this document ...
Up: Smoothing
Previous: Median Filter
Ruye Wang
2013-09-10
![]() and the variance
and the variance ![]() of all pixels
in the neighborhood
of all pixels
in the neighborhood ![]() of a given pixel
of a given pixel ![]() of the input image:
of the input image:
![\begin{displaymath}\mu=\frac{1}{N} \sum_{(i,j) \in W} x[i,j] \end{displaymath}](img35.png)
![\begin{displaymath}\sigma^2=\frac{1}{N} \sum_{(i,j) \in W} [x[i,j]-\mu]^2 \end{displaymath}](img36.png)
![\begin{displaymath}y[m,n]=\left\{ \begin{array}{ll}
x[m,n] & \mbox{if $\vert x[...
...mu\vert < \sigma T$} \mu & \mbox{else}
\end{array} \right. \end{displaymath}](img38.png)

![]() is replaced by the mean 7.1 from
the northeast neighborhood with minimum variance 105.
is replaced by the mean 7.1 from
the northeast neighborhood with minimum variance 105.