


Next: Median Filter
Up: Smoothing
Previous: Smoothing
The isolated pixels with gray values much different from its neighbors
can be considered as impulses corresponding to high spatial frequencies.
One way to get rid of this kind of noise is to use the average of a small
local region in the image so that the out-of-range gray levels can be
suppressed. Equivalently, this averaging operation in spatial domain
corresponds to low-pass filtering in the spatial frequency domain.
The averaging operation is a weighted sum of the pixels in a small
neighborhood and can be implemented by a common convolution with a kernel
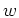 of certain shapes and values:
of certain shapes and values:
where
![$w[i,j]=w[-i,-i]$](img3.png) is a symmetric kernel of a limited size (typically
3x3, 5x5, 7x7, etc.). Some common kernels:
is a symmetric kernel of a limited size (typically
3x3, 5x5, 7x7, etc.). Some common kernels:
These convolution kernels can be considered as the approximations of some
continuous 2D functions such as a rectangular function
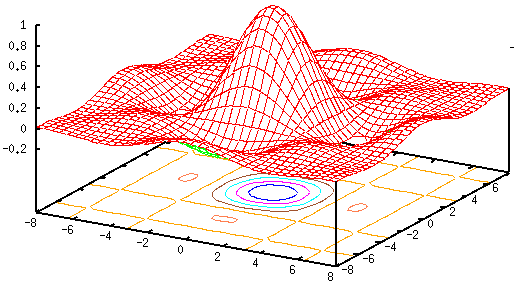
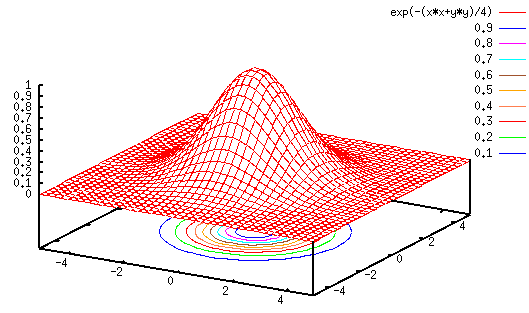
and a Gaussian function
Convolution with such functions in spatial domain 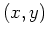 is equivalent
to the filtering in spatial frequency domain
is equivalent
to the filtering in spatial frequency domain 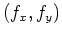 with the Fourier
transforms of the kernel functions:
with the Fourier
transforms of the kernel functions:
 and
and
In general the Gaussian function is a preferred method for the following
reasons:
- Rotational symmetric with no bias on any particular direction;
- Closer neighbors contribute more (larger weights) than those farther
away;
- The width of the function can be easily controlled;
- Fourier transform of Gaussian is also Gaussian so that the filtering
in frequency domain is smooth.
Weymouth-Overton's algorithm
- Define weights for each pixel
![$x[i,j]$](img15.png) in the neighborhood W of the pixel
in the neighborhood W of the pixel
![$x[m,n]$](img16.png) under consideration. The distance weight is defined as:
under consideration. The distance weight is defined as:
and the value weight is defined as:
where 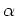 is a user specified parameter. The overall weight for pixel
is a user specified parameter. The overall weight for pixel ![$x[i,j]$](img15.png) is defined as
is defined as
Pixels close to ![$x[m,n]$](img16.png) in both distance and value will have larger weights.
in both distance and value will have larger weights.
- Replace
![$x[m,n]$](img16.png) by
by



Next: Median Filter
Up: Smoothing
Previous: Smoothing
Ruye Wang
2013-09-10
![]() of certain shapes and values:
of certain shapes and values:
![\begin{displaymath}y[m,n]=\sum \sum_{i,j \in w} w[i,j]\;x[m-i,n-j]
=\sum \sum_{i,j \in w} w[i,j]\;x[m+i,n+j] \end{displaymath}](img2.png)
![\begin{displaymath}w=\frac{1}{4}\left[ \begin{array}{cc} 1 & 1 1 & 1 \end{array} \right] \end{displaymath}](img4.png)
![\begin{displaymath}w=\frac{1}{6}\left[ \begin{array}{ccc} 0 & 1 & 0 1 & 2 & 1 \\
0 & 1 & 0 \end{array} \right] \end{displaymath}](img5.png)
![\begin{displaymath}w=\frac{1}{9}\left[ \begin{array}{ccc} 1 & 1 & 1 1 & 1 & 1 \\
1 & 1 & 1 \end{array} \right] \end{displaymath}](img6.png)
![\begin{displaymath}w=\frac{1}{10}\left[ \begin{array}{ccc} 1 & 1 & 1 1 & 2 & 1 \\
1 & 1 & 1 \end{array} \right] \end{displaymath}](img7.png)
![\begin{displaymath}w=\frac{1}{16}\left[ \begin{array}{ccc} 1 & 2 & 1 2 & 4 & 2 \\
1 & 2 & 1 \end{array} \right] \end{displaymath}](img8.png)

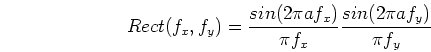
 and
and

![\begin{displaymath}w_d[i,j]=\frac{1}{1+\sqrt{(m-i)^2+(n-j)^2} \end{displaymath}](img17.png)
![\begin{displaymath}w_v[i,j]=\frac{1}{1+[x[i,j]-x[m,n]]^\alpha} \end{displaymath}](img18.png)
![\begin{displaymath}y[m,n]=\frac{\sum_{(i,j)\in W} w[i,j] x[i,j]}{\sum_{(i,j)\in W} w[i,j] } \end{displaymath}](img21.png)