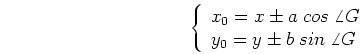Next: Generalized Hough transform
Up: hough
Previous: Detection of Circles
Here we assume the axes of the ellipses are in parallel with the coordinates
of the image space, i.e., the equations specifying the ellipses are in the
following standard form
where 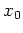 ,
, 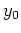 ,
, 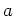 and
and 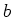 are four parameters which span a 4D parameter
Hough space. To use
are four parameters which span a 4D parameter
Hough space. To use 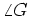 , consider
, consider
Now we only need to increment those elements in the parameter space that
satisfy both of the following equations
Solving these equations for 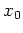 and
and 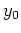 , we get
, we get
and the algorithm for detecting circles:
- For any pixel satisfying
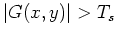 , increment all elements
satisfying the two simultaneous equations above;
, increment all elements
satisfying the two simultaneous equations above;
for all 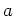 and all
and all 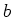
{
}
- In the parameter space, any element
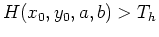 represents an ellipse detected in the image.
represents an ellipse detected in the image.



Next: Generalized Hough transform
Up: hough
Previous: Detection of Circles
Ruye Wang
2009-11-17
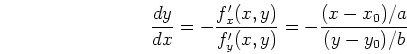
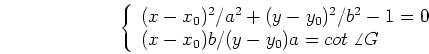
![]() and
and ![]() , we get
, we get
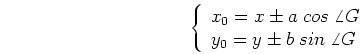
and all