Generalized Hough transform

Two possible difficulties may occur in the above Hough transform method: (a) the shape has to be described by an equation, and (b) the number of parameters $n$ (dimensions of the parameter space) may be high. Given the two equations:

$$\left\{ \begin{array}{l} f(x,y,\alpha_1,\cdots,\alpha_n)=0 \... ...\alpha_1,\cdots,\alpha_n) =cot\; \angle G \end{array} \right.$$

we still have to search the remaining $n-2$ dimensions of the parameter space. These two difficulties can be avoided by the generalized Hough transform shown below.

1. Preparation: build a table for the given shape
   • Prepare a table with $k$ entries each indexed by an angle $\phi_i$ ( $i=1, \cdots, K$) which increases from 0 to 180 degrees with increment $180/k$, where $k$ is the resolution of the gradient orientation (see below).

   • Define a reference point $(x_c, y_c)$ somewhere inside the 2D shape (e.g., the gravitational center). For each point $(x,y)$ on the boundary of the shape, find two parameters
     
     $$\left\{ \begin{array}{l} r=\sqrt{(x-x_c)^2+(y-y_c)^2} \\ \beta=tan^{-1} \;(y-y_c)/(x-x_c) \end{array} \right.$$
     
     
     and the gradient direction $\angle G$. Add the pair $(r, \beta)$ to the table entry with its $\phi$ closest to $\angle G$.

   • Prepare a 2D Hough array $H(x_c, y_c)$ initialized to 0.

   
   

   $$\begin{tabular}{c\vert\vert cccc}\hline $\phi_1=0$ & $(r,\... ...$ & $\cdots$ & $(r,\beta)_{k_{n_1}}$ \hline \end{tabular}$$
   
   

2. Detection of the shape and its locations in image

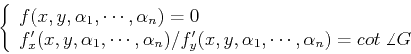
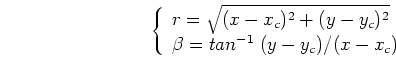
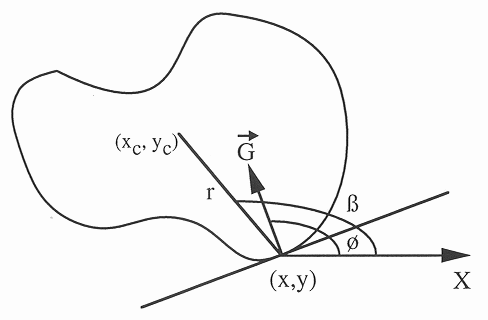
   For each image point $(x,y)$ with $\vert G(x,y)\vert > T_s$, find the table entry with its corresponding angle $\phi_j$ closest to $\angle G(x,y)$. Then for each of the $n_j$ pairs $(r, \beta)_i$ ( $i=1,\cdots,n_j$) in this table entry, find
   

   $$\left\{ \begin{array}{l} x_c=x+r \; cos \; \beta \\ y_c=y+r \; sin \; \beta \end{array} \right.$$
   
   
   and increment the corresponding element in the H array by 1:
   
   $$H(x_c,y_c)=H(x_c,y_c)+1$$
   
   

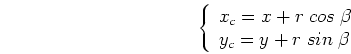
   All elements in the H table satisfying $H(x_c, y_c) > T_h$ represent the locations of the shape in the image.

   It is desirable to detect a certain 2D shape independent of its orientation and scale, as well as its location. To do so, two additional parameters, a scaling factor $S$ and a rotational angle $\theta$, are needed to describe the shape. Now the Hough space becomes 4-dimensional $H(x_c, y_c, S, \theta)$. The detection algorithm becomes the following:

   For each image point $(x,y)$ with $\vert G(x,y)\vert>T$, find the proper table entry with $\phi_j=\angle G(x,y)$. Then for each of the $n_j$ pairs $(r, \beta)_i$ ( $i=1,\cdots,n_j$) in this table entry, do the following for all $S$ and $\theta$: find
   

   $$\left\{ \begin{array}{l} x_c=x+r\;S\; cos (\beta+\theta) \\ y_c=y+r\;S\; sin (\beta+\theta) \end{array} \right.$$
   
   
   and increment the corresponding element in the 4D H array by 1:
   
   $$H(x_d,y_c,S,\theta)=H(x_c,y_c,S,\theta)+1$$
   
   

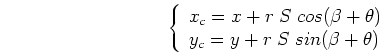
   All elements in the H table satisfying $H(x_c, y_c,S,\theta) > T_h$ represent the scaling factor $S$, rotation angle $\theta$ of the shape, as well as its reference point location $(x_c, y_c)$ in the image.