Histogram Equalization

To transform the gray levels of the image so that the histogram of the resulting image is equalized to become a constant:

$$h[i]= \mbox{constant},\;\;\;\;\;\;0\le i<L$$

The purposes:

• to equally make use of all available gray levels in the dynamic range;
• for further histogram specification.

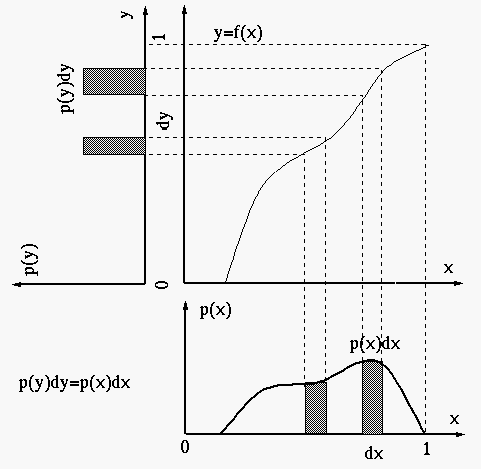
We first assume the pixel values are continuous in the range of $0<x<1$, and the mapping function $y=f(x)$ maps $x$ to $y$ also in the same range. We also assume all pixels within the gray scale interval $dx$ of the input image are mapped to the corresponding range $dy$ of the output image. As the number of pixels being mapped remains unchanged, we have

$$p(y)dy=p(x)dx$$

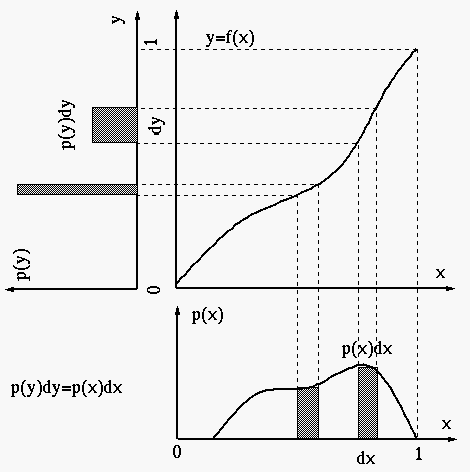
For the histogram of the output image to be equalized, it needs to be constant 1, i.e., $p(y)=1$, so that

$$\int_0^1 p(x)\;dx=\int_0^1 dy=1$$

We therefore have:

$$dy=p(x)dx,\;\;\;\mbox{or}\;\;\;\frac{dy}{dx}=p(x)$$

Integrating both sides, we get the mapping function $y=f(x)$ for the histogram equalization:

$$y=f(x)=\int_0^x p(u) du=P(x)-P(0)=P(x)$$

where $P(x)$ is the cumulative distribution of the gray levels of the input image:

$$P(x)=\int_0^x p(u) du, \;\;\;\;\;P(0)=0,\;\;\;\;\;\;P(1)=1$$

This histogram equalization mapping can be intuitively interpreted by the following:

• If $p(x)$ is low, $P(x)$ has a shallow slope, $dy$ will be narrow, causing $p(y)$ to be high, to keep $p(y)dy=p(x)dx$;
• If $p(x)$ is high, $P(x)$ has a steep slope, $dy$ will be wide, causing $p(y)$ to be low, to keep $p(y)dy=p(x)dx$.

For discrete gray levels, the gray level of the input $x$ takes one of the $L$ discrete values: $0\le x < L$, and the continuous mapping function becomes discrete:

$$y'[j]=H_x[j]\stackrel{\triangle}{=}\sum_{i=0}^j h_x[i]$$

where $h_x[i]$ and $H_x[j]$ are respectively the density and cumulative histogram of the input image $x$:

$$h_x[i]=\frac{n_i}{\sum_{i=0}^{L-1} n_i}=\frac{n_i}{N},\;\;\;\;\;\;\; \sum_{i=0}^{L-1} h_x[i]=1$$

and $n_i$ is the number of pixels with gray level $i$, and $N$ is the total number of pixels.

The resulting function $y'$ in the range $0 \le y' \le 1$ needs to be converted to the gray levels $0 \le y <L$ by either of the two ways:

1. 
   
   $$y_1=\lfloor (L-1)\;y' +0.5 \rfloor$$
   
   

2. 
   
   $$y_2=\lfloor (L-1) \;\frac{y'-y'_{min}}{1-y'_{min}}+0.5 \rfloor$$
   
   

where $\lfloor w \rfloor$ is the floor of a real number $w$ (the largest integer smaller than $w$), and adding $0.5$ is for proper rounding. Note that both conversions map $y'_{max}=1$ to the highest gray level $L-1$, the second conversion also maps $y'_{min}$ to 0 to stretch the gray levels of the output image to occupy the entire dynamic range $0 \le y <L$; i.e., the second method does gray scale stretch as well as histogram equalization.

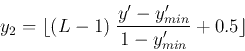
Example:

Assume the images have $N=64 \times 64=4096$ pixels in $L=8$ gray levels. The following table shows the equalization process corresponding to the two conversion methods above:

$x_i=i$	$n_i$	$h[i]=n_i/N$	$y'=H[i]$	$y_1$	$h_1$	$H_1$	$y_2$	$h_2$	$H_2$
0	790	0.19	0.19	$0.19\times 7\approx 1$	0.19	0.19	0	0.19	0.19
1	1023	0.25	0.44	$0.44\times 7\approx 3$	0.25	0.44	2	0.25	0.44
2	850	0.21	0.65	$0.65\times 7\approx 5$	0.21	0.65	4	0.21	0.65
3	656	0.16	0.81	$0.81\times 7\approx 6$			5	0.16	0.81
4	329	0.08	0.89	$0.89\times 7\approx 6$	0.24	0.89	6	0.08	0.89
5	245	0.06	0.95	$0.95\times 7\approx 7$			7
6	122	0.03	0.98	$0.98\times 7\approx 7$			7
7	81	0.02	1.00	$1.00\times 7=7$	0.11	1.00	7	0.11	1.00

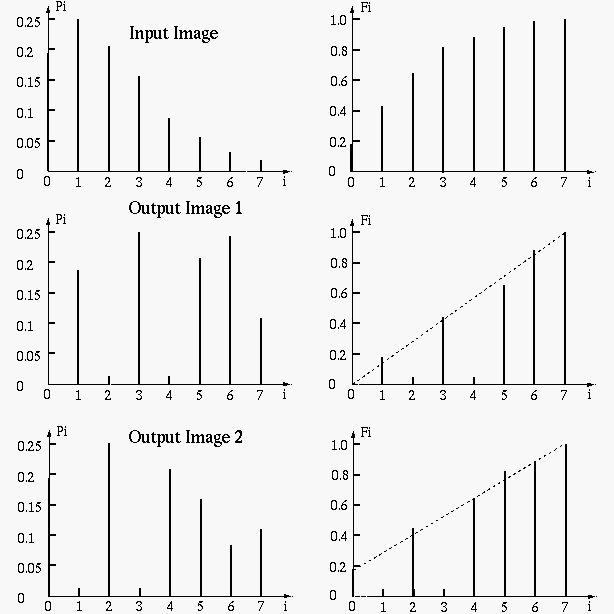
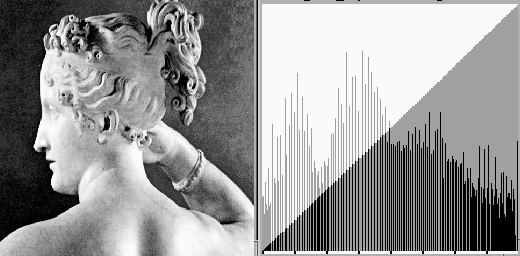
In the following example, the histogram of a given image is equalized. Although the resulting histogram may not look constant, but the cumulative histogram is a exact linear ramp indicating that the density histogram is indeed equalized. The density histogram is not guaranteed to be a constant because the pixels of the same gray level cannot be separated to satisfy a constant distribution.

Programming issues:

• Obtain the histogram of the input image:
  
  $$\par d=1.0/M/N; \par for (i=0; \;\;i<256;\;\;i++)\; \;h[i]=0... ...\;\;n<N;\;\;n++) \par \;\;\;\;\;\;\;h[x[m][n]]=h[x[m][n]]+d;$$
  
  

• Build lookup table:

  
  

  $$\par sum=0.0; \par for (i=0;\;\;i<256;\;\;i++)\;\;\{ \par \;\;\;\;sum=sum+h[i]; \par \;\;\;\;lookup[i]=sum*255; \par \} \par$$
  
  

• Image Mapping:

  
  

  $$\par for (m=0; \;\;m<M;\;\;m++) \par \;\;\;for (n=0; \;\;n<N;\;\;n++) \par \;\;\;\;\;\;y[m][n]=lookup[x[m][n]]; \par$$
  
  

Example: