


Next: Eigenvalues and eigenvectors
Up: algebra
Previous: Rank, trace, determinant, transpose,
A square matrix  is a Hermitian matrix iff it is equal to
its complex conjugate transpose
is a Hermitian matrix iff it is equal to
its complex conjugate transpose
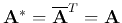 .
If a Hermitian matrix
.
If a Hermitian matrix
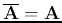 is real, it is a
symmetric matrix,
is real, it is a
symmetric matrix,
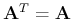 .
.
 is a unitary matrix iff
is a unitary matrix iff
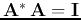 , i.e.,
its conjugate transpose is equal to its inverse
, i.e.,
its conjugate transpose is equal to its inverse
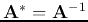 .
When a unitary matrix
.
When a unitary matrix
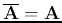 is real, it becomes an
orthogonal matrix,
is real, it becomes an
orthogonal matrix,
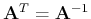 .
.
The column (or row) vectors
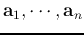 of a unitary matrix
of a unitary matrix
![${\bf A}=[{\bf a}_1,\cdots,{\bf a}_N]$](img101.png) are orthonormal, i.e. they are
both orthogonal and normalized, i.e.,
are orthonormal, i.e. they are
both orthogonal and normalized, i.e.,
As we will see later, any Hermitian matrix  can be converted to a
diagonal matrix
can be converted to a
diagonal matrix 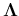 (or diagonalized) by a particular unitary
matrix
(or diagonalized) by a particular unitary
matrix 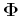 :
:
where 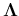 is a diagonal matrix, i.e., all its off diagonal elements
are 0.
is a diagonal matrix, i.e., all its off diagonal elements
are 0.
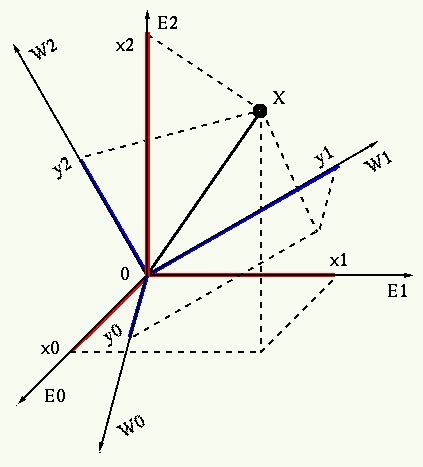
Given any unitary matrix  , we can define a unitary transform
of a vector
, we can define a unitary transform
of a vector
![${\bf x}=[x_1,\cdots,x_n]^T$](img39.png) :
:
When
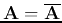 is real,
is real,
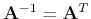 is an
orthogonal matrix and the corresponding transform is an orthogonal transform.
is an
orthogonal matrix and the corresponding transform is an orthogonal transform.
The first equation above is the forward transform and can be written
in component form as:
The transform coefficient is an inner product
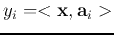 ,
representing the projection of vector
,
representing the projection of vector 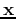 onto the ith column vector
onto the ith column vector
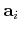 of the transform matrix
of the transform matrix  . The second equation is the
inverse transform and can also be written in component form as:
. The second equation is the
inverse transform and can also be written in component form as:
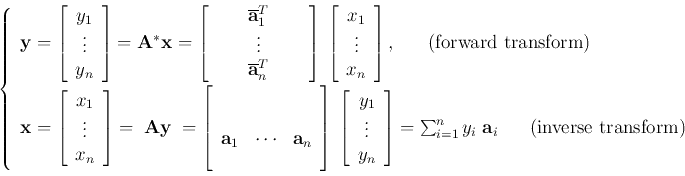
By this transform, vector 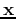 is represented as a linear combination
(weighted sum) of the
is represented as a linear combination
(weighted sum) of the 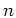 column vectors
column vectors
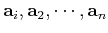 of matrix
of matrix  . Geometrically,
. Geometrically, 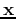 is a point in the n-dimensional space
spanned by these
is a point in the n-dimensional space
spanned by these 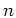 orthonormal basis vectors. Each coefficient (coordinate)
orthonormal basis vectors. Each coefficient (coordinate) 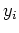 is the projection of
is the projection of 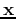 onto the corresponding basis vector
onto the corresponding basis vector 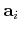 .
.
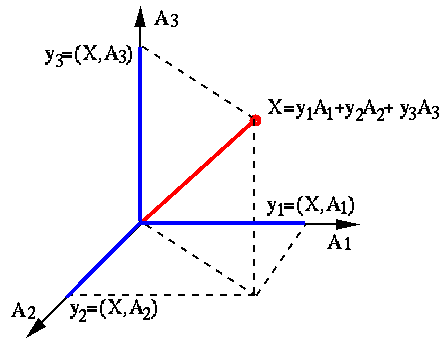
As the n-dimensional space can be spanned by the column vectors of any n by n
unitary (orthogonal) matrix, a vector 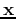 in the space can be represented by
any of such matrices, each defining a different transform.
in the space can be represented by
any of such matrices, each defining a different transform.
Examples:
A unitary (orthogonal) transform
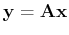 can be interpreted
geometrically as the rotation of the vector
can be interpreted
geometrically as the rotation of the vector 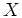 about the origin, or equivalently,
the representation of the same vector in a rotated coordinate system. A unitary
(orthogonal) transform
about the origin, or equivalently,
the representation of the same vector in a rotated coordinate system. A unitary
(orthogonal) transform
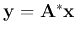 does not change the vector's
norm (length)
does not change the vector's
norm (length)
as
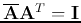 . This is the Parseval's identity that
indicates that the norm or length of a vector is conserved under any unitary
transform. If
. This is the Parseval's identity that
indicates that the norm or length of a vector is conserved under any unitary
transform. If 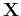 is interpreted as a signal, then its length
is interpreted as a signal, then its length
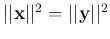 represents the total energy or information
contained in the signal, which is conserved during any unitary transform.
However, some other features of the signal may change, e.g., the signal may
be decorrelated and its total energy redistributed among its components after
the transform, which may be desirable in many applications.
represents the total energy or information
contained in the signal, which is conserved during any unitary transform.
However, some other features of the signal may change, e.g., the signal may
be decorrelated and its total energy redistributed among its components after
the transform, which may be desirable in many applications.
If 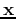 is a random vector with mean vector
is a random vector with mean vector 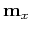 and covariance
matrix
and covariance
matrix 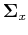 :
:
then its transform
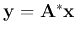 has the following mean vector and
covariance matrix:
has the following mean vector and
covariance matrix:
In general the unitary transform of any square matrix  by a unitary
matrix
by a unitary
matrix 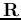 is
is



Next: Eigenvalues and eigenvectors
Up: algebra
Previous: Rank, trace, determinant, transpose,
Ruye Wang
2014-06-05
![]() is a Hermitian matrix iff it is equal to
its complex conjugate transpose
is a Hermitian matrix iff it is equal to
its complex conjugate transpose
![]() .
If a Hermitian matrix
.
If a Hermitian matrix
![]() is real, it is a
symmetric matrix,
is real, it is a
symmetric matrix,
![]() .
.
![]() is a unitary matrix iff
is a unitary matrix iff
![]() , i.e.,
its conjugate transpose is equal to its inverse
, i.e.,
its conjugate transpose is equal to its inverse
![]() .
When a unitary matrix
.
When a unitary matrix
![]() is real, it becomes an
orthogonal matrix,
is real, it becomes an
orthogonal matrix,
![]() .
.
![]() of a unitary matrix
of a unitary matrix
![]() are orthonormal, i.e. they are
both orthogonal and normalized, i.e.,
are orthonormal, i.e. they are
both orthogonal and normalized, i.e.,
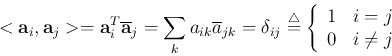
![]() , we can define a unitary transform
of a vector
, we can define a unitary transform
of a vector
![]() :
:
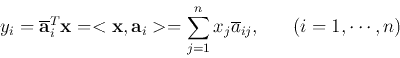
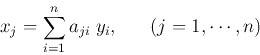

![]() in the space can be represented by
any of such matrices, each defining a different transform.
in the space can be represented by
any of such matrices, each defining a different transform.
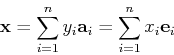

![]() can be interpreted
geometrically as the rotation of the vector
can be interpreted
geometrically as the rotation of the vector ![]() about the origin, or equivalently,
the representation of the same vector in a rotated coordinate system. A unitary
(orthogonal) transform
about the origin, or equivalently,
the representation of the same vector in a rotated coordinate system. A unitary
(orthogonal) transform
![]() does not change the vector's
norm (length)
does not change the vector's
norm (length)
![]() is a random vector with mean vector
is a random vector with mean vector ![]() and covariance
matrix
and covariance
matrix ![]() :
:
![]() by a unitary
matrix
by a unitary
matrix ![]() is
is