Rank, trace, determinant, transpose, and inverse of matrices

Let ${\bf A}$ be an $n \times n$ square matrix:

$${\bf A}=[{\bf a}_1,\cdots,{\bf a}_n]=\left[ \begin{array}{c... ...} & a_{n2} & \cdots & a_{nn} \end{array} \right]_{n\times n}$$

where

$${\bf a}_j=\left[ \begin{array}{c} a_{1j}\\ a_{2j}\\ \vdots\\ a_{nj} \end{array}\right]$$

is the jth column vector and $[a_{i1}\;a_{i2}\;\cdots\;a_{in}]$ is the ith row vector.

The n rows span the row space of ${\bf A}$ and the n columns span the column space of ${\bf A}$. The dimensions of these two spaces are the same and called the rank of ${\bf A}$:

$$R=rank({\bf A}) \leq n$$

The determinant of $A$ is denoted by $det({\bf A}) = \vert {\bf A} \vert$ and we have

$$\vert {\bf A}{\bf B} \vert=\vert{\bf A}\vert\; \vert{\bf B}\vert$$

$rank({\bf A}) < n$ if and only if $det({\bf A})=0$.

The trace of $A$ is defined as the sum of its diagonal elements:

$$tr({\bf A}) = \sum_{i=1}^n a_{ii}$$

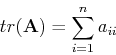
The transpose of a matrix ${\bf A}$, denoted by ${\bf A}^T$, is obtained by switching the positions of elements $a_{ij}$ and $a_{ji}$ for all $i,j \in \{1,\cdots,n\}$. In other words, the ith column of ${\bf A}$ becomes the ith row of ${\bf A}^T$, or equivalently, the ith row of ${\bf A}$ becomes the ith column of ${\bf A}^T$:

$${\bf A}^T=[{\bf a}_1 \cdots {\bf a}_n]^T= \left[ \begin{array}{c} {\bf a}_1^T \\ \vdots\\ {\bf a}_n^T \end{array} \right]$$

where vector ${\bf a}_i$ is the ith column of ${\bf A}$ and its transpose ${\bf a}_i^T$ is the ith row of ${\bf A}^T$.

If ${\bf AB}={\bf BA}={\bf I}$, where ${\bf I}$ is an identity matrix:

$${\bf I}=diag[1,\cdots,1]=\left[ \begin{array}{cccc} 1 & 0 &... ...\cdot & \cdot & \cdot 0 & 0 & \cdot & 1 \end{array} \right]$$

then ${\bf B}={\bf A}^{-1}$ is the inverse of ${\bf A}$. ${\bf A}^{-1}$ exists iff $det({\bf A}) \neq 0$, i.e., $rank({\bf A}) = n$.

For any two matrices ${\bf A}$ and ${\bf B}$, we have

$$({\bf A}{\bf B})^T={\bf B}^T {\bf A}^T, \;\;\;\;\;\;\;\;\;\;... ...-1} \;\;\;\;\;\;\;\;\;\;\; ({\bf A}^{-1})^T=({\bf A}^T)^{-1}$$