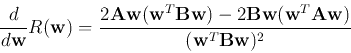Next: Positive/Negative (semi)-definite matrices
Up: algebra
Previous: Hermitian and unitary matrices
For any matrix 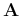 , if there exist a vector
, if there exist a vector 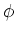 and a value
and a value 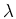 such that
such that
then 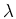 and
and 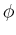 are called the eigenvalue and
eigenvector of matrix
are called the eigenvalue and
eigenvector of matrix 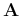 , respectively. Note that the eigenvector
, respectively. Note that the eigenvector
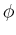 is not unique but up to any scaling factor, i.e, if
is not unique but up to any scaling factor, i.e, if 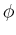 is the eigenvector of
is the eigenvector of 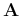 so is
so is 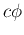 with any costant
with any costant 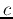 .
Typically for the uniqueness of
.
Typically for the uniqueness of 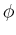 , we keep if normalized with
, we keep if normalized with
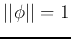 .
.
To obtain 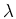 , rewrite the above equation as
, rewrite the above equation as
which is a homogeneous equation system. For this system to have non-zero solution
for 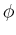 , the determinant of its coefficient matrix has to be zero:
, the determinant of its coefficient matrix has to be zero:
Solving this 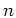 th order equation of
th order equation of 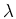 , we get
, we get 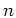 eigenvalues
eigenvalues
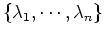 . Substituting each
. Substituting each 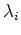 back into
the equation system, we get the corresponding eigenvector
back into
the equation system, we get the corresponding eigenvector 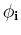 .
We can put all
.
We can put all 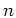 equations
equations
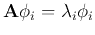 together and have
together and have
or in a more compact matrix form,
where
are the diagonal eigenvalue matrix and eigenvector matrix, respectively.
The spectrum of an 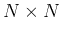 square matrix
square matrix 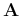 the set of
its eigenvalues
the set of
its eigenvalues
 . The spectral radius
of
. The spectral radius
of 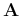 , denoted by
, denoted by 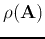 , is the maximum of the absolute
values of the elements of its spectrum:
, is the maximum of the absolute
values of the elements of its spectrum:
The absolute value of a complex number 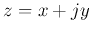 is
is
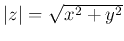 ,
the Euclidean distance between
,
the Euclidean distance between 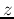 and the origin of the complex plane.
If all eigenvalues are sorted such that
and the origin of the complex plane.
If all eigenvalues are sorted such that
 then
then
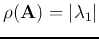 .
.
The trace and determinant of 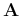 can be obtained from its eigenvalues
can be obtained from its eigenvalues
It can also be shown that
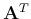 has the same eigenvalues and eigenvectors as
has the same eigenvalues and eigenvectors as 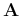 .
.
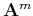 has the same eigenvectors as
has the same eigenvectors as 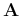 , but its eigenvalues
are
, but its eigenvalues
are
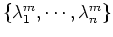 , where
, where 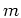 is a positive integer.
is a positive integer.
- In particular when
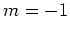 , i.e., the eigenvalues of
, i.e., the eigenvalues of 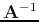 are
are
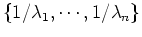 .
.
The eigenvalues and eigenvectors of a matrix are invariant under any unitary
transform
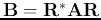 . To prove this, we first assume
. To prove this, we first assume
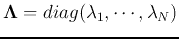 and
and 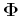 are the
eigenvalue and eigenvector matrices of a square matrix
are the
eigenvalue and eigenvector matrices of a square matrix 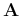 :
:
and
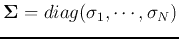 and
and 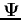 are the
eigenvalue and eigenvector matrices of
are the
eigenvalue and eigenvector matrices of
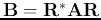 , a
unitary transform of
, a
unitary transform of 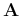 :
:
Left-multiplying 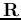 on both sides we get the eigenequation of
on both sides we get the eigenequation of 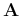
with same eigenvalue and igenvector matrices
If 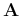 is Hermitian (symmetric if real), such as a covarance matrix,
then all of its eigenvalues
is Hermitian (symmetric if real), such as a covarance matrix,
then all of its eigenvalues 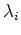 's are real and all eigenvectors
's are real and all eigenvectors
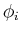 's are orthogonal and can be normalized (orthonormal):
's are orthogonal and can be normalized (orthonormal):
and the eigenvector matrix 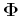 is unitary (orthogonal if
is unitary (orthogonal if 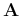 is real):
is real):
and we have
Left and right multiplying by 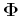 and
and
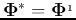 respectively on the two sides, we get
respectively on the two sides, we get
The generalized eigenvalue problem of two symmetric matrices
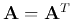 and
and
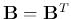 is to find a scalar
is to find a scalar 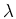 and the corresponding vector
and the corresponding vector
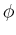 for the following equation to hold:
for the following equation to hold:
or in matrix form
The eigenvalue and eigenvector matrices 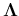 and
and 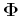 can be found in the following steps.
can be found in the following steps.
The Rayleigh quotient of two symmetric matrices 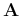 and
and 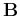 is a function of a vector
is a function of a vector 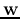 defined as:
defined as:
To find the optimal 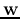 corresponding to the extremum (maximum or minimum)
of
corresponding to the extremum (maximum or minimum)
of 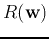 , we find its derivative with respect to
, we find its derivative with respect to 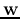 :
:
Setting it to zero we get
The second equation can be recognized as a generalized eigenvalue problem with
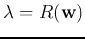 being the eigenvalue and and
being the eigenvalue and and 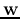 the corresponding
eigenvector. Solving this we get the vector
the corresponding
eigenvector. Solving this we get the vector
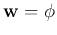 corresponding
to the maximum/minimum eigenvalue
corresponding
to the maximum/minimum eigenvalue
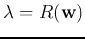 , which maximizes/minimizes
the Rayleigh quotient.
, which maximizes/minimizes
the Rayleigh quotient.



Next: Positive/Negative (semi)-definite matrices
Up: algebra
Previous: Hermitian and unitary matrices
Ruye Wang
2014-06-05
![]() , if there exist a vector
, if there exist a vector ![]() and a value
and a value ![]() such that
such that
![]() , rewrite the above equation as
, rewrite the above equation as
![\begin{displaymath}
{\bf A}[{\bf\phi_1},\cdots,{\bf\phi}_n]
=[\lambda_1 {\bf\p...
... \vdots \\
0 & 0 & \cdots & \lambda_n
\end{array} \right]
\end{displaymath}](img157.png)
![]() square matrix
square matrix ![]() the set of
its eigenvalues
the set of
its eigenvalues
![]() . The spectral radius
of
. The spectral radius
of ![]() , denoted by
, denoted by ![]() , is the maximum of the absolute
values of the elements of its spectrum:
, is the maximum of the absolute
values of the elements of its spectrum:
![]() can be obtained from its eigenvalues
can be obtained from its eigenvalues
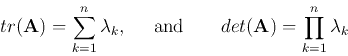
![]() . To prove this, we first assume
. To prove this, we first assume
![]() and
and ![]() are the
eigenvalue and eigenvector matrices of a square matrix
are the
eigenvalue and eigenvector matrices of a square matrix ![]() :
:
![]() is Hermitian (symmetric if real), such as a covarance matrix,
then all of its eigenvalues
is Hermitian (symmetric if real), such as a covarance matrix,
then all of its eigenvalues ![]() 's are real and all eigenvectors
's are real and all eigenvectors
![]() 's are orthogonal and can be normalized (orthonormal):
's are orthogonal and can be normalized (orthonormal):
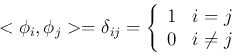
![\begin{displaymath}
{\bf A}={\bf\Phi} {\bf\Lambda}{\bf\Phi}^*=[{\bf\phi}_1,\cdo...
...} \right]
=\sum_{i=1}^n \lambda_i {\bf\phi}_i {\bf\phi}_i^*
\end{displaymath}](img188.png)
![]() and
and
![]() is to find a scalar
is to find a scalar ![]() and the corresponding vector
and the corresponding vector
![]() for the following equation to hold:
for the following equation to hold:
![]() is symmetric,, it can be diagonalized by its orthogonal
eigenvector matrix
is symmetric,, it can be diagonalized by its orthogonal
eigenvector matrix ![]() :
:
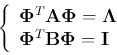
![]() and
and ![]() is a function of a vector
is a function of a vector ![]() defined as:
defined as: