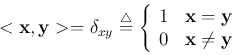The norm of vector ![]() in a vector space
in a vector space ![]() is a non-negative
real value representing intuitively the length, size, or magnitude of the
vector. Specifically, the norm of vector
is a non-negative
real value representing intuitively the length, size, or magnitude of the
vector. Specifically, the norm of vector ![]() satisfies:
satisfies:
Consider the norms in the following common vector fields.
If the vector ![]() is a real number in the real space
is a real number in the real space ![]() ,
then its norm is simply its absolute value
,
then its norm is simply its absolute value
![]() .
.
If the vector
![]() is a complex number in the complex space
is a complex number in the complex space
![]() , then its norm is simply its modulus
, then its norm is simply its modulus
![]() .
.
If
![]() is a vector in an n-D vector space
is a vector in an n-D vector space
![]() or
or
![]() , then we can use the p-norms
defined as
, then we can use the p-norms
defined as
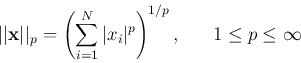
The commonly used p-norms are for ![]() ,
, ![]() , and
, and ![]() :
:
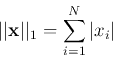
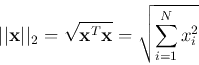
The distance between two points
![]() in a vector
space is defined as the norm of the difference
in a vector
space is defined as the norm of the difference
![]() .
.
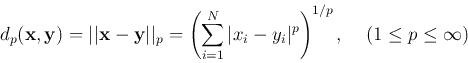
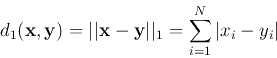
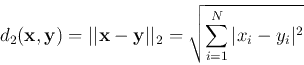

The three curves or surfaces correspond to the iso-distances to the center
point, formed by all points with equal distances to the point at the center,
blue for ![]() , black for
, black for ![]() , and red for
, and red for ![]() .
.
Two different vectors ![]() and
and ![]() are orthogonal to each
other if their inner product is zero
are orthogonal to each
other if their inner product is zero
![]() . If they are also
normalized with
. If they are also
normalized with
![]() , then they are orthonormal,
, then they are orthonormal,