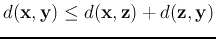- Vector addition maps any two vectors
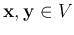 to another vector
to another vector
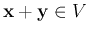 satisfying the following
properties:
satisfying the following
properties:
- Commutativity:
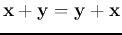 .
.
- Associativity:
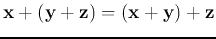 .
.
- Existence of zero: there is a vector
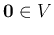 such that:
such that:
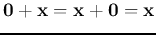 .
.
- Existence of inverse: for any vector
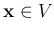 , there is
another vector
, there is
another vector 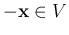 such that
such that
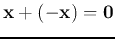 .
.
- Commutativity:
- Scalar multiplication maps a vector
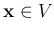 and a real
or complex scalar
and a real
or complex scalar 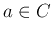 to another vector
to another vector
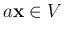 with the following properties:
with the following properties:
-
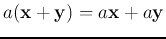 .
.
-
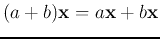 .
.
-
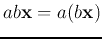 .
.
-
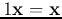 .
.
-
-
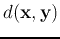 iff
iff
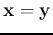
-
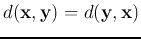
-