Next: Single-Supply Op Amps and Up: Chapter 5: Operational Amplifiers Previous: Operational Amplifier
The full analysis of the op-amp circuits as shown in the three examples
above may not be necessary if only the voltage gain is of interest. This
is based on the assumptions that





Now consider the following typical op-amp circuits:
 |
(32) |
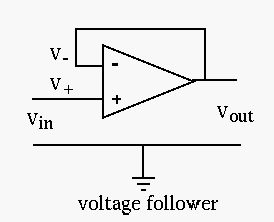
 is the same as the input, why can't we replace this
op-amp circuit by a piece of wire?
is the same as the input, why can't we replace this
op-amp circuit by a piece of wire?
As 


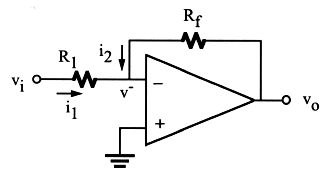
 i.e. i.e. |
(33) |
In general, 



 |
(34) |
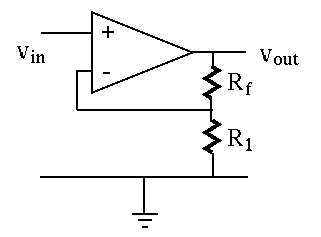
 i.e. i.e. |
(35) |
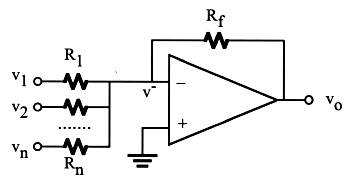
Apply KCL to 
 i.e. i.e. |
(36) |
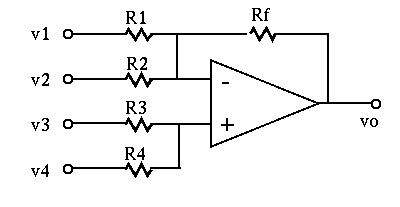
It can be shown that (see here) the output is some algebraic sum of the inputs with both positive and negative coefficients:
 |
(37) |
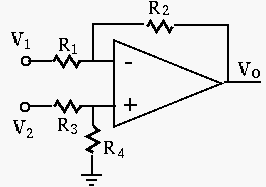
We note that the differential amplifier is similar to an inverting
amplifier but with an additional input to the non-inverting side.
We first define



 i.e. i.e. |
(38) |
 |
(39) |
 |
(40) |
If one of the two inputs, connected to a constant reference voltage

 , the output is a inversely scaled version of
, the output is a inversely scaled version of  positively shifted by a constant value
positively shifted by a constant value  :
:
 where where |
(41) |
 , the output is a scaled version of
, the output is a scaled version of  negatively shifted by
negatively shifted by  :
:
 where where |
(42) |
We further consider some special cases:
 and
and  , then we get
, then we get
 |
(43) |
 (open circuit, and
(open circuit, and  can be any value), then
can be any value), then  ,
and the circuit is a combination of inverter and a non-inverter amplifiers:
,
and the circuit is a combination of inverter and a non-inverter amplifiers:
 |
(44) |
 , then
, then
 , the circuit becomes the
follower:
, the circuit becomes the
follower:
 |
(45) |
 and
and
 , then the circuit becomes the inverter:
, then the circuit becomes the inverter:
 |
(46) |
 ,
,
 , and
, and  , then the circuit becomes the
non-inverter:
, then the circuit becomes the
non-inverter:
 |
(47) |
It is likely that both inputs are subjected to some common noise

 |
(48) |
 |
(49) |
 )
while amplify the differential-mode signal (e.g.,
)
while amplify the differential-mode signal (e.g.,  and
and  ).
).
The main drawback of the differential amplifier is that its input
impedance (
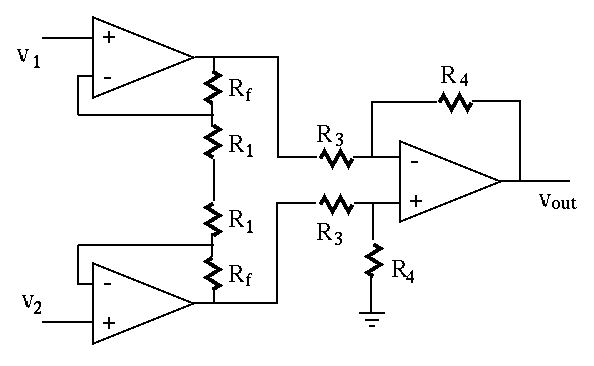
Recall that the output resistance of a non-inverting amplifier is
very low, its output voltage will not affected by the load circuit,
here the differential amplifier whose its input resistance (

 |
(50) |
 |
(51) |
 can be combined to become
can be combined to become  ,
i.e.,
,
i.e.,  , then the output can be written as:
, then the output can be written as:
 |
(52) |
Alternatively, we consider the current going from 





 |
(53) |
 |
(54) |
 |
(55) |
 |
(56) |
 ,
,
 (open-circuit), i.e., the
circuit has a unit voltage gain. However, if an external resistor
(open-circuit), i.e., the
circuit has a unit voltage gain. However, if an external resistor
 (
( ) is connected to the circuit, the gain can be greater
up to 1000.
) is connected to the circuit, the gain can be greater
up to 1000.
Without feedback, the output of an op-amp is





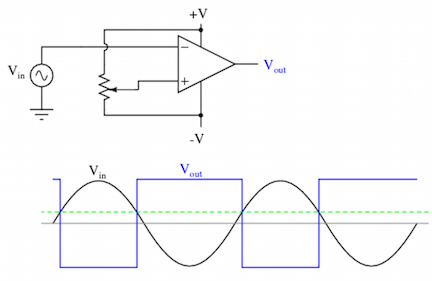
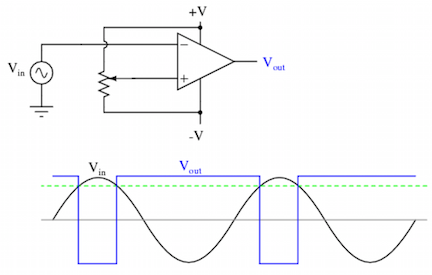
These two possible outputs, positive and negative, can be treated as “1”
and “0” of the binary system. The figure shows an A/D converter built by
three op-amps to measure voltage 
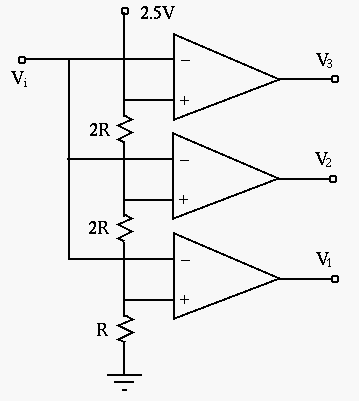
Due to the voltage divider, the input voltages to the three op-amps are, respectively, 2.5V, 1.5V and 0.5V. The output of these op-amps are listed below for each of the input voltage levels. A digital logic circuit (a decoder) can convert the 3-bit output of the op-amps to the 2-bit binary representation.
 |
(57) |
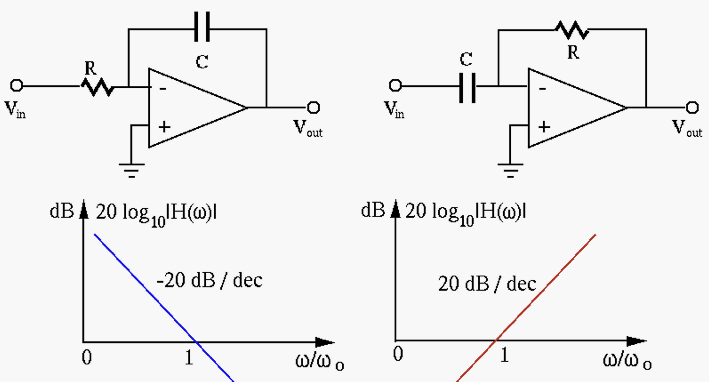
Integrator
In time domain, as 

 i.e., i.e., |
(58) |
 . In frequency domain, we have:
. In frequency domain, we have:
 |
(59) |
Differentiator
If we swap the resistor and the capacitor, we get in time domain:
 i.e., i.e., |
(60) |
 |
(61) |
A proportional-integral-derivative (PID) controller can be implemented as shown. The output of the circuit is a linear combination of the signal together with its integral and derivative:
 |
(62) |
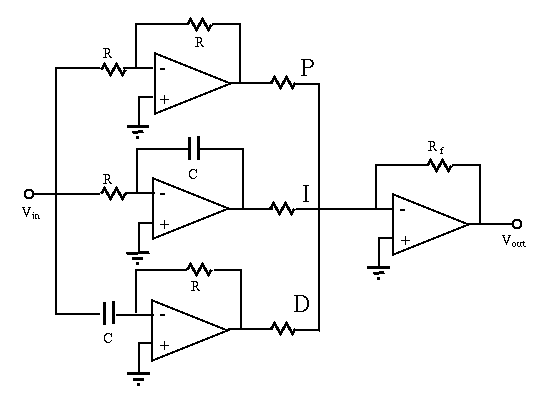
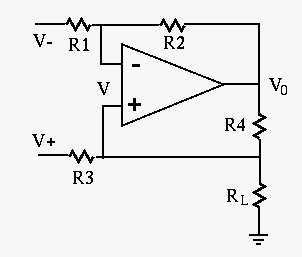
Assuming




 |
(63) |
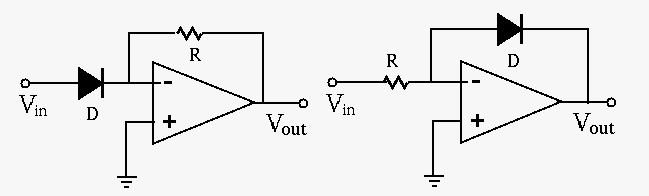
Based on the relationship between the current through and voltage across a diode and the virtual ground assumption, we can show that the output voltage of the exponential amplifier (left) is approximately an exponential function of the input voltage, and the output voltage of the logarithmic amplifier (right) is approximately a logarithmic function of the input voltage:
 |
(64) |
 and
and  .)
.)
Many op-amp circuits practically used can be found here.