Next: Higher order systems Up: Chapter 6: Active Filter Previous: Wien bridge
The transition between the pass-band and stop-band of a first order
filter with cut-off frequency


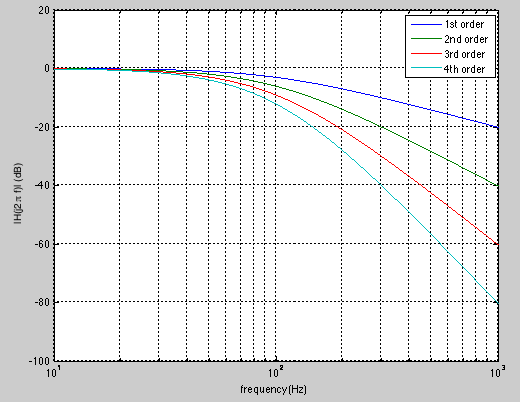
The FRF of a first-order low-pass filter of unit gain is:
 (67)
(67)
 such filters in series is (assuming they are well
buffered with no loading effect):
such filters in series is (assuming they are well
buffered with no loading effect):
 (68)
(68)
 can be
found by solving the following equation
can be
found by solving the following equation
 (69)
(69)
 (70)
(70)
Example: Design an 4th order LP filter with

 (71)
(71)
 . If
. If
 ,
then
,
then
 (72)
(72)
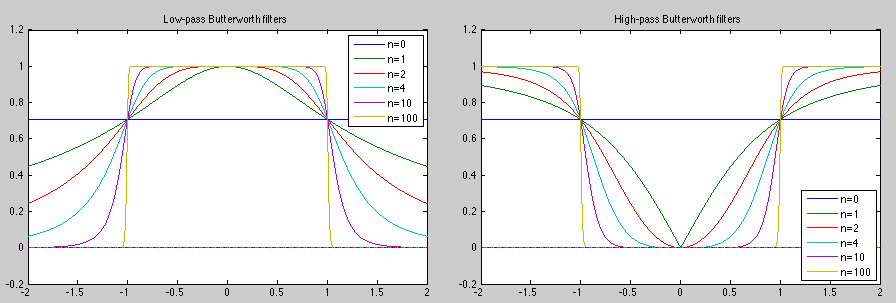
The Butterworth filters have the property that the passing
band is flat. The magnitude of the FRF of an nth order low-pass
Butterworth filter with cut-off frequency 
 (73)
(73)
 is the cut-off frequency at which
is the cut-off frequency at which
 .
The transition between the pass-band and stop-band is controlled by the
order
.
The transition between the pass-band and stop-band is controlled by the
order  . In general, higher order corresponds to more rapid transition.
Specially, when
. In general, higher order corresponds to more rapid transition.
Specially, when  ,
,  , and
, and  , we have
, we have
 ,
,
 is an all-pass filter.
is an all-pass filter.
 , the Butterworth filter is the regular first-order filter:
, the Butterworth filter is the regular first-order filter:
 (74)
(74)
 , the Butterworth filter becomes an ideal low-pass
filter:
, the Butterworth filter becomes an ideal low-pass
filter:
 (75)
(75)
The magnitude of the FRF of an nth order high-pass Butterworth filter
with cut-off frequency 
 (76)
(76)
Now we consider the implementation of a Butterworth filter. For
simplicity, in the following we assume the frequency is normalized
by the cut-off frequency 


 (77)
(77)
 from its magnitude
from its magnitude  .
To do so, we first consider the transfer function (TF)
.
To do so, we first consider the transfer function (TF)  in the
s-domain corresponding to the FRF, which is the same as
in the
s-domain corresponding to the FRF, which is the same as  when
when  , i.e.,
, i.e.,
 . Now the equation
above can be written as
. Now the equation
above can be written as
 (78)
(78)
 and
and  , and separate them so that those on the left s-plane are
the poles of
, and separate them so that those on the left s-plane are
the poles of  (stable and causal), while those on the right
s-plane belong to
(stable and causal), while those on the right
s-plane belong to  (stable and anti-causal).
(stable and anti-causal).
The roots of the denominator can be found by solving the equation
 (79)
(79)
 solutions on the unit circle in
either of the two different forms depending on whether
solutions on the unit circle in
either of the two different forms depending on whether  is even
or odd:
is even
or odd:
 (80)
(80)
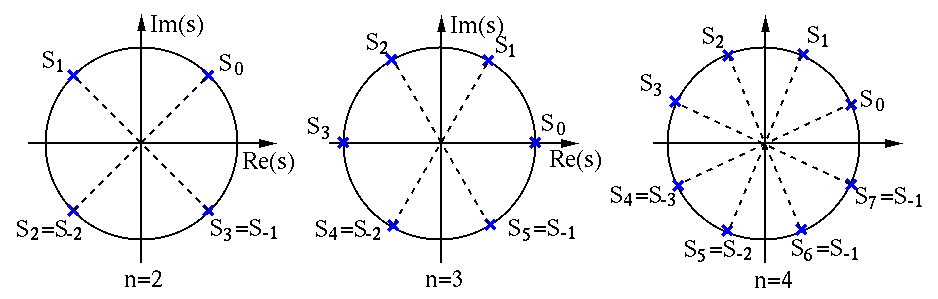
 is even,
is even,
 (81)
(81)
 roots form
roots form  complex conjugate pairs around the unit
circle of the s-plane. Corresponding to each of the
complex conjugate pairs around the unit
circle of the s-plane. Corresponding to each of the  roots
roots
 (
(
 ), there is another root
), there is another root
 that is its complex conjugate:
that is its complex conjugate:
 (82)
(82)
 to be a pole of
to be a pole of  , it needs to be on
the left s-plane, i.e.,
, it needs to be on
the left s-plane, i.e.,
 (83)
(83)
 can be found in terms of its
can be found in terms of its  poles on the left s-plane:
poles on the left s-plane:
 |
 |
 |
|
 |
 |
(84) |
 is the ceiling of
is the ceiling of  , and we have
used the fact that
, and we have
used the fact that
 (85)
(85)
 is odd,
is odd,
 (86)
(86)
 roots contain
roots contain  and
and
 , as well as
, as well as
 complex conjugate pairs. Corresponding to each root
complex conjugate pairs. Corresponding to each root
 (
(
 ), there is another root
), there is another root  that is its complex
conjugate:
that is its complex
conjugate:
 (87)
(87)
 to be a pole of
to be a pole of  , it needs to be on the left s-plane, i.e.,
, it needs to be on the left s-plane, i.e.,
 (88)
(88)
 can be found in terms of its
can be found in terms of its  poles on the left s-plane:
poles on the left s-plane:
 |
 |
 |
|
 |
 |
(89) |
Specifically, here we find the transfer function 

 ,
,  ,
,
 , the four roots are
, the four roots are
 (
( ):
):
 (90)
(90)
 and
and  on the left s-plane are the roots of
on the left s-plane are the roots of
 :
:
 |
 |
 |
|
 |
 |
(91) |
 .
.
 ,
,  ,
,
 , the six roots are
, the six roots are
 (
( )
)
 (92)
(92)
 (93)
(93)
 ,
,  , and
, and  on the left s-plane
are the roots of
on the left s-plane
are the roots of  :
:
 |
 |
 |
|
 |
 |
(94) |
 .
.
 ,
,  ,
,
 , the eight roots are
, the eight roots are
 (
( ).
Evaluating
).
Evaluating
 for
for  and
and  , we get the
coefficients of the two first order terms
, we get the
coefficients of the two first order terms
 and
and
 .
.
 (95)
(95)
 ,
,  ,
,
 , the 10 roots are
, the 10 roots are
 (96)
(96)
 for
for  and
and  , we get the
coefficients of the two first order terms
, we get the
coefficients of the two first order terms
 and
and
 , and we get
, and we get
 (97)
(97)
 ,
,  ,
,
 , the 12 roots are
, the 12 roots are
 (98)
(98)
 for
for  ,
,  , and
, and  ,
we get the coefficients of the three first order terms
,
we get the coefficients of the three first order terms
 ,
,
 , and
, and
 .
.
 (99)
(99)
 if
if  is even, and an additional first order system in the form of
is even, and an additional first order system in the form of
 if
if  is odd. The block diagrams below are for the 5th
and 6th order Butterworth filters:
is odd. The block diagrams below are for the 5th
and 6th order Butterworth filters:
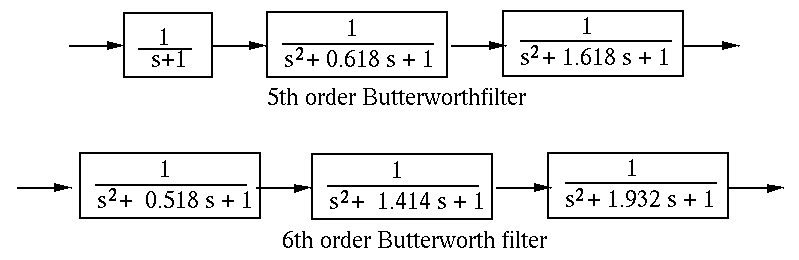
The first order filter in the cascade of the Butterworth filter can be realized by the first order op-amp low-pass circuit shown above with
 (100)
(100)
 . If we let
. If we let  , we get
, we get
 .
.
The second order systems in the cascade can be implemented as a Sallen-Key low-pass filter with
 (101)
(101)
 . If we let
. If we let  for simplicity,
we get
for simplicity,
we get
 (102)
(102)
 (103)
(103)
A High-pass Butterworth filter can be similarly implemented with the only difference that all first and second order systems in the cascade are high-pass filters
 (104)
(104)
 (105)
(105)
To convert the results obtained above for normalized cut-off frequency








