CMOS Digital Logic Circuits

The Logic family is composed of different types of digital logic circuits:

• RTL
• DTL
• TTL
• CMOS

Both the p-channel MOSFET (pMOS) and n-channel MOSFET (nMOS) can be treated as a switch between its drain $D$ and source $S$ controlled by the voltage $V_{gs}$ between gate $G$ and source $S$. When $V_{gs}>V_{Tn}$ (e.g., $V_{Tn}=1\;V$) for nMOS and $V_{gs}\le V_{Tp}$ (e.g., $V_{Tp}=-1\;V$) for pMOS, the circuit is a short-circuit because of the low resistance between $D$ and $S$; otherwise, the circuit is an open-circuit due to the large resistance between $D$ and $S$. A circuit composed of both types of MOSFET transistors is called a complementary MOS or CMOS circuit, which is widely used in digital systems.

• Logic AND can be implemented by a series combination of two MOS transistors, which conducts electricity if both are turned on and conducting.

• Logic OR can be implemented by a parallel combination of two MOS transistors, which conduct electricity if either of them is turned on and conducting.

Due to such logic properties of the series and parallel connections of the MOS transistors, various logic circuits can be constructed to realize any arbitrary logic function $f(a,b,\cdots,x)$ by two complementary networks of MOS transistors:

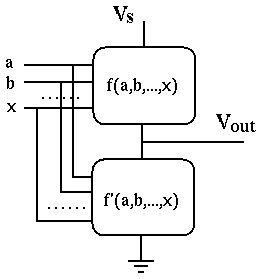
• The pull-up network composed of pMOS transistors connected to the positive voltage source $V_s$ so that the circuit will conduct.

• The pull-down network composed of nMOS transistors connected to ground, so that the circuit will conduct.

These two pull-up and pull-down networks will turn on and off alternatively, depending on the input variables of the logic function. If the pull-up circuit representing the function $f(a,b,\cdots,x)$ is conduting and the pull-down circuit representing the negation of the function $f'(a,b,\cdots,x)$ is cut-off, the voltage at output is pulled up to a high voltage (logical 1) indicatng the function is true; when the pull-up circuit is cut-off and the pull-down circuit is conducting, the voltage at output is pulled down to a low voltage (logical 0) indicating the function is false.

The specific circuits of the pull-up and pull-down networks are based on De Morgan's Law which states: the negation (complement) $f'$ of a logic function $f$ can be found by negating the logical operations (turn AND to R and OR to AND) as well as the variables in a function. For example, given a logic function $f(a,b,c)=(a'+b')c$, we can find its negation by De Morgan's law:

$$f'(a,b,c)=[(a'+b')c]'=(a'+b')'+c'=ab+c'$$ (183)

Here are the CMOS implementations of some simple logic functions:

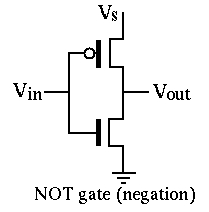
• Negation

  The NOT gate is implemented by a pull-up circuit composed of only a pMOS transistor and its complementary pull-down circuit composed of only a nMOS transistor:

  

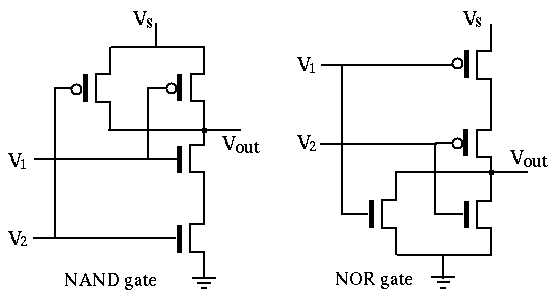
• Logic NAND:

  The pull-up function is $f(V_1,V_2)=(V_1 V_2)'=V_1'+V_2'$, the pull-down function is $f'=V_1\;V_2$.

• Logic NOR:

  The pull-up function $f(V_1,V_2)=(V_1+V_2)'=V_1'\,V_2'$, the pull-down function is $f'=V_1+V_2$.

  $$\begin{tabular}{cc\vert\vert c\vert c\vert c\vert c} \\ \hline & ... ...& 0 \\ 1 & 0 & 0 & 1 & 1 & 0 \\ 1 & 1 & 1 & 1 & 0 & 0 \\ \hline \end{tabular}$$ (184)

  

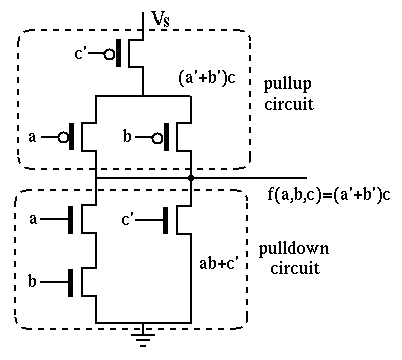
• A random logical function $f(a,b,c)=(a'+b')c$:

  The pull-up network implements the given function $f$ while the pull-down network implements its negation $f'(a,b,c)=ab+c'$: